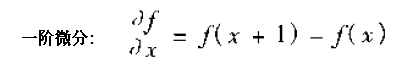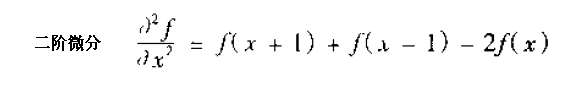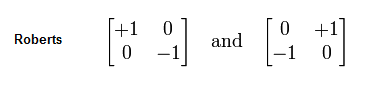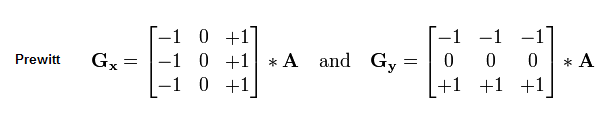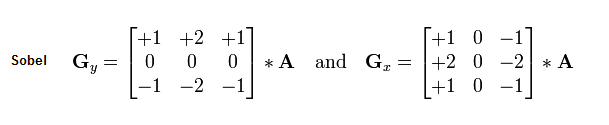图像锐化 边缘检测的一些基础知识

互联网兴起， 生活节奏飞速，快餐成了favorite。理论学习也受到了巨大的冲击，一些不明所以的冰冷的公式和整段可以运行的代码是很多人的最爱。使得原本应该沉静的软件开发变得异常浮躁，（当然很多博客也成了帮凶：））今天就要融化冰雪， 说说代码以外的东西，说说冰雪初成的原因。

 

锐化的概念，我们从锐度开始谈起。很多人都以为锐度就是Sharpness,其实在数字图像的领域， 这个锐度更准确的说法是acutance, 万能的Wiki给出了 acutance 的标准的定义。In photography, acutance is the edge contrast of an image。 这句话已经说的非常清晰了， 锐度的意思就是边缘的对比度。（这里的边缘指的就是图像中的物件的边缘）。

下面是一组很形象的图：（无图无真相）

从这一组图可以看出， 这里的锐度从左到右逐渐提高了。锐度的提高会使图像像素不增加的基础上造成提高清晰度的假象。

那么这样的锐化效果如何实现呢？那一个个传统的算子(Operator)是如何可以工作的呢？

我们慢慢来展开，回到锐度的本意来看， 锐度就是边缘的对比度， 提高锐度（锐化）就是把边缘的对比度提高，所以我们的工作就变成了

a)找到有差异的相邻的像素     （这个东东是不是就是检测到边缘，我们一直说的边缘检测）

b)增加有差异的像素的对比度

为了方便说明问题， 我们把寻找边缘的问题从一维的情形开始定义，我们把这样的所谓的差异定义成一种数学模型：

不要看到数学分析就慌张了， 其实这里还是非常容易理解，这里的一阶微分就是水平扫面相邻像素的灰度值差， 而二阶的只是在前面的灰度差上又做了一个微分， 就是再求了一次灰度差。

说实话看到这样的模型的时候，第一反应就是Win32的一个接口GradientFill, GradientFill会把像素渐变的平铺在一定的矩形中。或者说在某个方向上的f(x)就类似于f(x)=ax+b;的直线。 如果我们使用一阶微分的模型来度量， 那样的微分就永远是f(x+1)-f(x)=a!!!也就是说这里的渐变的像素都需要增强！但是增强a，换句话说大家的灰度差在进行了这个增强操作之后还是没有效果的。但是如果二阶的模型的话，就是再f(x)=a上再做一次微分也就是0, 就是不需要做任何的增强！很容易地看出还是有差异的。 继续联想到如果我们一个图里面只有一个区域是 GradientFill的， 而其他的区域都是随机的颜色， 那这里的一阶微分就会改变这里的大片的 GradientFill区域和周围颜色的差异， 可能这样的效果不是我们需要的。

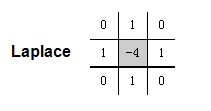
从这里的一阶和二阶的对比马上可以看出， 如果使用二阶的模型的话， 能够更为准确的把握出边缘，同时去除那种稳定渐变的情况， 而一阶明显的拉大了边缘的范围， 使边缘变得更粗了(当然也可以通过后期的threshold来去除)。所以总的来说二阶的模型还是更为受欢迎。在这样的背景下，Laplace算子诞生就不难理解了.这个就是一个明显的二阶微分在水平和竖直方向的和!

我们来看看它的模版：

其实这个公式的推导异常容易就是 laplace ={ f(x+1,y)+f(x-1,y)+2f(x,y) } +  { f(x,y-1) + f(x, y+1) - 2f(x, y)}

                                                          = f (x-1,y) + f(x+1,y) + f(x,y-1) + f(x, y+1) - 4f(x, y);

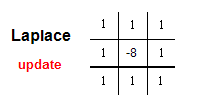
是不是赫然就是前面的公式。更常见的一个 Laplace算子也如是：

 

那就是在原来的基础上加上和对角线的微分， 就是在原来基础上加上了

f(x-1,y-1)+f(x-1,y+1)+f(x+1,y-1)+f(x+1,y+1)-4f(x,y); 套用老罗的一句话， 好理解吧：）

 

在二阶之前的一阶的微分算子可能就更容易理解一些， 比如做常见的Roberts算子：

这个就是对角的微分的差的和啦， f(x,y)+f(x+1,y)-f(x,y+1)-f(x+1,y+1)

这里的prewitt就是把微分扩展成了Δf(x,y) = (f(x+h)-f(x-h))/2h的case, 而这里的h=1; 在他的基础上Sobel又更进了一步，他把像素的微分加上了权重的概念

可以看到，离带处理点越近的点具有更高的权重，这样能够更准确的定位到边缘的所在。

 

到这里， 我们大致了解了边缘检测的一些基本的逻辑， 完了之后， 如何继续锐化呢？其实这个在前面一篇文章中都有实现了， 我们还是以Laplace的算子为例, 我们要处理原来的f(x,y)和现在得到的laplace(x,y)之间的关系， 到底是加法还是减法呢？？利用原来的sample我们继续计算得到：

 明显的看出，在这样的情形下， 减法还是获得了更大的对比值， 也就是获得了更好的效果， 所以我们选用了减法， 当然这里的理论性的说明就是， 如果这个3x3模版的最中央的数字为正数，那么他就是加法，如果是负数，那么就是减法。这样的说法很容易得到了验证， 由此， 我们可以方便的得出结论， Laplace算子如果要用来锐化图像的话， 可以表示成为

到这里没有太多的想法去试验其他的边缘检测和锐化， 就把laplace的这个模版试了一下， 效果不是很好， 没有前面一篇文章的效果那么好， 呵呵