- 剑指 Offer II 113. 课程顺序(中等 图 bfs 拓扑排序 数组 哈希表)
风雨中de宁静
图搜索算法
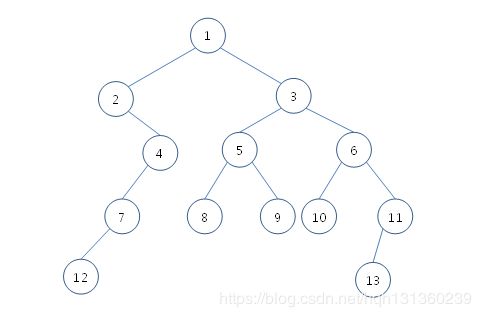
剑指OfferII113.课程顺序现在总共有numCourses门课需要选,记为0到numCourses-1。给定一个数组prerequisites,它的每一个元素prerequisites[i]表示两门课程之间的先修顺序。例如prerequisites[i]=[ai,bi]表示想要学习课程ai,需要先完成课程bi。请根据给出的总课程数numCourses和表示先修顺序的prerequisites
- 剑指 Offer II 061. 和最小的 k 个数对
炫云云
大数据算法和数据结构leetcode算法python
剑指OfferII061.和最小的k个数对给定两个以升序排列的整数数组nums1和nums2,以及一个整数k。定义一对值(u,v),其中第一个元素来自nums1,第二个元素来自nums2。请找到和最小的k个数对(u1,v1),(u2,v2)…(uk,vk)。示例1:输入:nums1=[1,7,11],nums2=[2,4,6],k=3输出:[1,2],[1,4],[1,6]解释:返回序列中的前3对
- 数组作为HashMap的键
南京鼎山电子设备维修张师傅
学习Java的一些记录java算法开发语言
1、数组的hashcode是根据地址引用计算的。2、Arrays.hashcode静态方法能够根据数组的内容创建相应的hashcode。3、hashmap用数组做key时用的是地址引用计算的的hashcode,所以应避免使用数组为键。如果一定要用数组来作为map的key值的话,有两种方法:1,将数组转化为string2,用list代替记录自:力扣-剑指OfferII033.变位词组,链接力扣。
- 剑指offer笔试刷题(1):树专题
weixin_35837473
1.输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)遍历A找到与B根结点相同的位置,子结构是从根结点到叶子节点相同。思路1:1.先考虑特殊情况,如果指针为空则错误。2定义一个子函数,功能是判断是否是子结构,然后主函数从根结点到叶子结点遍历。3return递归的布尔型值,如果最后return的是&&则递归终止条件是true关系不大,只要有一个是false,r
- 离散化+树状数组解决逆序对问题
算法吴神
算法数据结构
1、问题来源剑指Offer51.数组中的逆序对2、解决办法:《1》使用暴力法,双层for循环,时间复杂度为O(n^2)《2》借助归并排序来实现。归并排序的原理就是将一个序列无限二分,直到每个部分只有一个元素,那这部分就是有序的了,再对两个元素进行比较排序,分别放入左半部分和右半部分;对左半部分和右半部分分别进行有序插入后合并,如此反复......例如,我们现在有两个部分:现在进行合并,对两个部分的
- 算法研究员技术图谱和学习路径
执于代码
开发者职业加速服务算法学习
一、基础阶段:构建算法与数学根基数据结构与基础算法数据结构:数组、链表、栈、队列、哈希表、树(二叉搜索树、堆、字典树)、图等。基础算法:排序(快速排序、堆排序)、查找(二分查找)、递归与分治、贪心算法、简单动态规划(背包问题)、字符串匹配(KMP、Rabin-Karp)、图遍历(BFS/DFS)等。实践方法:通过LeetCode等平台刷题(如“剑指Offer”系列),掌握算法原理与代码实现。数学基
- HJ48 从单向链表中删除指定值的节点
张紫娃
算法题链表数据结构java
牛客华为机试题库【题号HJ开头】(重点看)牛客在线编程算法篇【题号NC开头】剑指offer【题号JZ开头】力扣1)原题链接2)已有题解3)代码packagelinklist;importjava.io.BufferedReader;importjava.io.IOException;importjava.io.InputStreamReader;importjava.util.Arrays;/**
- 剑指Offer(第二版)面试题10:斐波那契数列
温柔狠角色
面试题笔试题剑指Offer剑指Offer斐波那契数列跳台阶
(尊重劳动成果,转载请注明出处:http://blog.csdn.net/qq_25827845/article/details/71933891冷血之心的博客)
- 《剑指offer》详解-Python
2401_86984695
python数据结构算法
()O()O()|递归依次交换左右子树即可|Done||20.包含min函数的栈|Medium|O(n)O(n)O(n)|建一个辅助栈,保存当前数的最小值|ToDo||28.数组中出现次数超过一半的数字|Medium|O(n);O(logn)O(n);O(logn)O(n);O(logn)|遍历数组;从中间向两边展开|Done||29.最小的k个数|Medium|O(nlogn);O(n)O(nl
- 深度优先搜索(DFS)——算法详解与Java实例
ktkiko11
Java算法深度优先
在之前的剑指offer系列大数问题中遇到了深度优先搜索(DFS)的问题,此处特做出详细讲解与说明。什么是DFS(深度优先搜索)?深度优先搜索(DFS,Depth-FirstSearch)是一种算法,它用来遍历或搜索树、图或其他数据结构。它的核心思想是沿着某条路径尽可能地向前探索,直到不能再继续为止,然后回溯到上一个节点,继续探索其他路径。想象一下你在迷宫里走路,你会选择一条路尽量往前走,走到尽头发
- 剑指offer II 001.整数除法
青城丶梦远
剑指offerleetcode算法职场和发展
剑指OfferII001.整数除法整数除法题目链接题目要求:给定两个整数a和b,求它们的除法的商a/b,要求不得使用乘号‘*’、除号‘/’以及求余符号‘%’。注意:整数除法的结果应当截去(truncate)其小数部分,例如:truncate(8.345)=8以及truncate(-2.7335)=-2假设我们的环境只能存储32位有符号整数,其数值范围是[−231,231−1]。本题中,如果除法结果
- 28岁开始零基础学前端,这些血的教训你一定要避免
2501_90336583
前端
写了一个Vue动态表单组件,发布到NPM上。模仿Vue1.0版本写了一个MiniVue,这让我对Vue的理解达到了源码级别。写了几篇关于Vue的文章。计算机理论知识计算机理论知识决定了一个程序员的天花板(在国内还得加上英语)。数据结构与算法算法看了《剑指offer题解》、《Leetcode题解》这两本书,还是挺有用的,也有刷到的题面试正好碰上了的。编译原理、计算机原理由于编译原理和计算机原理是看的
- 剑指 Offer II 002. 二进制加法
常某某的好奇心
数据结构
comments:trueedit_url:https://github.com/doocs/leetcode/edit/main/lcof2/%E5%89%91%E6%8C%87%20Offer%20II%20002.%20%E4%BA%8C%E8%BF%9B%E5%88%B6%E5%8A%A0%E6%B3%95/README.md剑指OfferII002.二进制加法题目描述给定两个01字符串a
- 剑指Offer|LCR 046.二叉树的右视图
阿月浑子の
剑指Offer算法算法javascript
LCR046.二叉树的右视图给定一个二叉树的根节点root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。示例1:输入:[1,2,3,null,5,null,4]输出:[1,3,4]示例2:输入:[1,null,3]输出:[1,3]示例3:输入:[]输出:[]提示:二叉树的节点个数的范围是[0,100]-1000){letnode=queue1.shift();//移除
- 剑指offer_edition2刷题记录
jiandandian_
数据结构与算法java开发语言
剑指offer_edition2刷题记录写在前面:此博客记录刷剑指offer题中遇到的困难和总结,以及过程中难以理解的地方,其中*代表需要过段时间回过头再看的题Q7重建二叉树*(20210421)Q8二叉树的下一个节点(原书涉及到指针,暂时跳过)Q9两个栈实现一个队列附加题两个队列实现一个栈Q10斐波那契数列附加题:青蛙跳台阶附加题:快速排序Q11旋转数组的最小数字*(20210424)Q12矩阵
- 《C语言入门100例》(第2例) 给定 n,求 1 + 2 + 3 + ... + n 的和给定 n,求 1 + 2 + 3 + ... + n 的和
leapold_Z
c++leetcode
【第02题】给定n,求1+2+3+…+n的和|四种解法文章目录主要知识点习题1.剑指Offer64.求1+2+…+n题目描述初见思路代码2.SumProblem题目描述初见3.剑指Offer57-II.和为s的连续正数序列题目描述初见思路代码总结主要知识点计算时注意数值计算在计算机内的溢出。与理论计算不同,算法设计中要时刻注意数值计算溢出的情况,以计算n∗(n+1)/2n*(n+1)/2n∗(n+
- 剑指Offer|LCR 033.字母异位词分组
阿月浑子の
剑指Offer算法javascript算法
LCR033.字母异位词分组给定一个字符串数组strs,将变位词组合在一起。可以按任意顺序返回结果列表。**注意:**若两个字符串中每个字符出现的次数都相同,则称它们互为变位词。示例1:输入:strs=["eat","tea","tan","ate","nat","bat"]输出:[["bat"],["nat","tan"],["ate","eat","tea"]]示例2:输入:strs=[""]
- 剑指Offer|LCR 032.有效的字母异位词
阿月浑子の
剑指Offer算法javascript算法
LCR032.有效的字母异位词给定两个字符串s和t,编写一个函数来判断它们是不是一组变位词(字母异位词)。注意:若*s*和*t*中每个字符出现的次数都相同且字符顺序不完全相同,则称*s*和*t*互为变位词(字母异位词)。示例1:输入:s="anagram",t="nagaram"输出:true示例2:输入:s="rat",t="car"输出:false示例3:输入:s="a",t="a"输出:fa
- 数据结构 1
五花肉村长
数据结构算法开发语言c语言visualstudio
1.什么是数据结构数据结构(DataStructure)是计算机存储和组织数据的方式,是指相互之间存在的一种或多种特定关系的数据元的集合。2.什么是算法算法(Algorithm)就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。3.数据结构和算法的书籍资料学习完数据结构知识,可以去看《剑指offer》和《
- 《剑指offer第二版》面试题7:重建二叉树(java)
castlet
题目描述输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果都不包含重复数字。例如,输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建的二叉树为:1/\23//\456\/78解题思路:以前序遍历序列A:{1,2,4,7,3,5,6,8}和中序遍历序列B:{4,7,2,1,5,3,8,6}为例。前序遍历的
- 剑指offer 面试题05. 替换空格
Hubhub
题目描述leetcode地址代码classSolution{public:stringreplaceSpace(strings){stringans="";for(autoe:s){if(e==''){ans+="%20";}else{ans+=e;}}returnans;}};
- 面试题 链表相交 -剑指offer简单
努力搬砖的小王
日常杂记链表leetcode数据结构
面试题链表相交题目链接给你两个单链表的头节点headA和headB,请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回null。图示两个链表在节点c1开始相交:题目数据保证整个链式结构中不存在环。注意,函数返回结果后,链表必须保持其原始结构。示例1:输入:intersectVal=8,listA=[4,1,8,4,5],listB=[5,0,1,8,4,5],skipA=2,ski
- 代码随想录算法训练营第八天| 344.反转字符串 541. 反转字符串II 剑指Offer 05.替换空格 151.翻转字符串里的单词 剑指Offer58-II.左旋转字符串
书痴熊
代码随想录训练营算法leetcode
Leetcode344.反转字符串思路分析:反转字符串直观思路是对称交换两端的字符,即双指针法。代码实现:classSolution{public:voidreverseString(vector&s){inti=0,j=s.size()-1;while(istr:return"".join(reversed(s.split()))Leetcode剑指Offer58-II.左旋转字符串思路分析:直
- 剑指offer----C语言版----第六天
姬如祎
剑指offerleetcode算法职场和发展c语言数据结构
目录1.用栈实现队列1.1题目描述1.2栈和队列的基础知识1.3思路分析2.扩展题目——用队列实现栈2.1题目描述2.2思路分析1.用栈实现队列原题链接:剑指Offer09.用两个栈实现队列-力扣(LeetCode)https://leetcode.cn/problems/yong-liang-ge-zhan-shi-xian-dui-lie-lcof/submissions/1.1题目描述用两个
- 力扣刷题记录(一)剑指Offer(第二版)
乘凉~
求职过程记录leetcode链表算法
1、本栏用来记录社招找工作过程中的内容,包括基础知识学习以及面试问题的记录等,以便于后续个人回顾学习;暂时只有2023年3月份,第一次社招找工作的过程;2、个人经历:研究生期间课题是SLAM在无人机上的应用,有接触SLAM、Linux、ROS、C/C++、DJIOSDK等;3、参加工作后(2021-2023年)岗位是嵌入式软件开发,主要是服务器开发,Linux、C/C++、网络编程、docker容
- 剑指offer-顺序打印矩阵
yyming
题目:输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字,例如,如果输入如下4X4矩阵:12345678910111213141516则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.解题思路:定义矩阵最大最小值,然后从第一行第一个到第一行最后一个访问,从右列第二个到最后一个访问,依次类推;假设每次访问周期为一个圈,内部为剩下没有访问的矩阵;可
- 剑指offer 48- 礼物的最大价值
顾子豪
在一个m×n的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于0)你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格直到到达棋盘的右下角。给定一个棋盘及其上面的礼物,请计算你最多能拿到多少价值的礼物?注意:m,n>0样例:输入:[[2,3,1],[1,7,1],[4,6,1]]输出:19解释:沿着路径2→3→7→6→1可以得到拿到最大价值礼物。分析:(1)状态表示:dp
- 求1+2+3+...+n
Waitt_
剑指OFFERC++
剑指OFFER题6------按牛客网通过率排序时间:2018.10.16.2036作者:Waitt题目求1+2+3+…+n,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。时间限制:1秒空间限制:32768K热度指数:128539解答1+2+3+…+n的公式结果为:(n2+n)/2;由于题目要求不可使用一些语句,则考虑利用mat
- 力扣基础速攻题单(排位刷分适用)
0
leetcode算法职场和发展
Leetcode速攻题单一部分:1.算法入门100讲系列,C语言入门系列算法零基础100讲1.2的幂2.3的幂3.4的幂4.斐波那契数5.第N个泰波那契数6.剑指offer.求1+2+…+n7.单调数列8.最富有客户的资产总量9.二进制矩阵中的特殊位置10.翻转图像11.旋转图像12.转置矩阵13.将一维数组转变为二维数组14.判断矩阵经轮转后是否一致15.二维网络迁移16.杨辉三角17.杨辉三角
- 【C++】二维数组传参方式
虚拟笔记使
C++c++开发语言
最近刚开始刷剑指offer,刚做到第三题的时候,发现C++二维数组的传参方式和C语言略有些不同,所以在这篇博客中,会列出C/C++常见的二维数组传参方式。(本方式和代码都是基于vs环境所编写)一.C语言二维数组传参方式C语言二维数组传参一般有三个方式。1.指针形式接收#includevoidPrint1(int*parr,introws,intcols)//指针,行数,列数{for(inti=0;
- Spring的注解积累
yijiesuifeng
spring注解
用注解来向Spring容器注册Bean。
需要在applicationContext.xml中注册:
<context:component-scan base-package=”pagkage1[,pagkage2,…,pagkageN]”/>。
如:在base-package指明一个包
<context:component-sc
- 传感器
百合不是茶
android传感器
android传感器的作用主要就是来获取数据,根据得到的数据来触发某种事件
下面就以重力传感器为例;
1,在onCreate中获得传感器服务
private SensorManager sm;// 获得系统的服务
private Sensor sensor;// 创建传感器实例
@Override
protected void
- [光磁与探测]金吕玉衣的意义
comsci
这是一个古代人的秘密:现在告诉大家
信不信由你们:
穿上金律玉衣的人,如果处于灵魂出窍的状态,可以飞到宇宙中去看星星
这就是为什么古代
- 精简的反序打印某个数
沐刃青蛟
打印
以前看到一些让求反序打印某个数的程序。
比如:输入123,输出321。
记得以前是告诉你是几位数的,当时就抓耳挠腮,完全没有思路。
似乎最后是用到%和/方法解决的。
而今突然想到一个简短的方法,就可以实现任意位数的反序打印(但是如果是首位数或者尾位数为0时就没有打印出来了)
代码如下:
long num, num1=0;
- PHP:6种方法获取文件的扩展名
IT独行者
PHP扩展名
PHP:6种方法获取文件的扩展名
1、字符串查找和截取的方法
1
$extension
=
substr
(
strrchr
(
$file
,
'.'
), 1);
2、字符串查找和截取的方法二
1
$extension
=
substr
- 面试111
文强chu
面试
1事务隔离级别有那些 ,事务特性是什么(问到一次)
2 spring aop 如何管理事务的,如何实现的。动态代理如何实现,jdk怎么实现动态代理的,ioc是怎么实现的,spring是单例还是多例,有那些初始化bean的方式,各有什么区别(经常问)
3 struts默认提供了那些拦截器 (一次)
4 过滤器和拦截器的区别 (频率也挺高)
5 final,finally final
- XML的四种解析方式
小桔子
domjdomdom4jsax
在平时工作中,难免会遇到把 XML 作为数据存储格式。面对目前种类繁多的解决方案,哪个最适合我们呢?在这篇文章中,我对这四种主流方案做一个不完全评测,仅仅针对遍历 XML 这块来测试,因为遍历 XML 是工作中使用最多的(至少我认为)。 预 备 测试环境: AMD 毒龙1.4G OC 1.5G、256M DDR333、Windows2000 Server
- wordpress中常见的操作
aichenglong
中文注册wordpress移除菜单
1 wordpress中使用中文名注册解决办法
1)使用插件
2)修改wp源代码
进入到wp-include/formatting.php文件中找到
function sanitize_user( $username, $strict = false
- 小飞飞学管理-1
alafqq
管理
项目管理的下午题,其实就在提出问题(挑刺),分析问题,解决问题。
今天我随意看下10年上半年的第一题。主要就是项目经理的提拨和培养。
结合我自己经历写下心得
对于公司选拔和培养项目经理的制度有什么毛病呢?
1,公司考察,选拔项目经理,只关注技术能力,而很少或没有关注管理方面的经验,能力。
2,公司对项目经理缺乏必要的项目管理知识和技能方面的培训。
3,公司对项目经理的工作缺乏进行指
- IO输入输出部分探讨
百合不是茶
IO
//文件处理 在处理文件输入输出时要引入java.IO这个包;
/*
1,运用File类对文件目录和属性进行操作
2,理解流,理解输入输出流的概念
3,使用字节/符流对文件进行读/写操作
4,了解标准的I/O
5,了解对象序列化
*/
//1,运用File类对文件目录和属性进行操作
//在工程中线创建一个text.txt
- getElementById的用法
bijian1013
element
getElementById是通过Id来设置/返回HTML标签的属性及调用其事件与方法。用这个方法基本上可以控制页面所有标签,条件很简单,就是给每个标签分配一个ID号。
返回具有指定ID属性值的第一个对象的一个引用。
语法:
&n
- 励志经典语录
bijian1013
励志人生
经典语录1:
哈佛有一个著名的理论:人的差别在于业余时间,而一个人的命运决定于晚上8点到10点之间。每晚抽出2个小时的时间用来阅读、进修、思考或参加有意的演讲、讨论,你会发现,你的人生正在发生改变,坚持数年之后,成功会向你招手。不要每天抱着QQ/MSN/游戏/电影/肥皂剧……奋斗到12点都舍不得休息,看就看一些励志的影视或者文章,不要当作消遣;学会思考人生,学会感悟人生
- [MongoDB学习笔记三]MongoDB分片
bit1129
mongodb
MongoDB的副本集(Replica Set)一方面解决了数据的备份和数据的可靠性问题,另一方面也提升了数据的读写性能。MongoDB分片(Sharding)则解决了数据的扩容问题,MongoDB作为云计算时代的分布式数据库,大容量数据存储,高效并发的数据存取,自动容错等是MongoDB的关键指标。
本篇介绍MongoDB的切片(Sharding)
1.何时需要分片
&nbs
- 【Spark八十三】BlockManager在Spark中的使用场景
bit1129
manager
1. Broadcast变量的存储,在HttpBroadcast类中可以知道
2. RDD通过CacheManager存储RDD中的数据,CacheManager也是通过BlockManager进行存储的
3. ShuffleMapTask得到的结果数据,是通过FileShuffleBlockManager进行管理的,而FileShuffleBlockManager最终也是使用BlockMan
- yum方式部署zabbix
ronin47
yum方式部署zabbix
安装网络yum库#rpm -ivh http://repo.zabbix.com/zabbix/2.4/rhel/6/x86_64/zabbix-release-2.4-1.el6.noarch.rpm 通过yum装mysql和zabbix调用的插件还有agent代理#yum install zabbix-server-mysql zabbix-web-mysql mysql-
- Hibernate4和MySQL5.5自动创建表失败问题解决方法
byalias
J2EEHibernate4
今天初学Hibernate4,了解了使用Hibernate的过程。大体分为4个步骤:
①创建hibernate.cfg.xml文件
②创建持久化对象
③创建*.hbm.xml映射文件
④编写hibernate相应代码
在第四步中,进行了单元测试,测试预期结果是hibernate自动帮助在数据库中创建数据表,结果JUnit单元测试没有问题,在控制台打印了创建数据表的SQL语句,但在数据库中
- Netty源码学习-FrameDecoder
bylijinnan
javanetty
Netty 3.x的user guide里FrameDecoder的例子,有几个疑问:
1.文档说:FrameDecoder calls decode method with an internally maintained cumulative buffer whenever new data is received.
为什么每次有新数据到达时,都会调用decode方法?
2.Dec
- SQL行列转换方法
chicony
行列转换
create table tb(终端名称 varchar(10) , CEI分值 varchar(10) , 终端数量 int)
insert into tb values('三星' , '0-5' , 74)
insert into tb values('三星' , '10-15' , 83)
insert into tb values('苹果' , '0-5' , 93)
- 中文编码测试
ctrain
编码
循环打印转换编码
String[] codes = {
"iso-8859-1",
"utf-8",
"gbk",
"unicode"
};
for (int i = 0; i < codes.length; i++) {
for (int j
- hive 客户端查询报堆内存溢出解决方法
daizj
hive堆内存溢出
hive> select * from t_test where ds=20150323 limit 2;
OK
Exception in thread "main" java.lang.OutOfMemoryError: Java heap space
问题原因: hive堆内存默认为256M
这个问题的解决方法为:
修改/us
- 人有多大懒,才有多大闲 (评论『卓有成效的程序员』)
dcj3sjt126com
程序员
卓有成效的程序员给我的震撼很大,程序员作为特殊的群体,有的人可以这么懒, 懒到事情都交给机器去做 ,而有的人又可以那么勤奋,每天都孜孜不倦得做着重复单调的工作。
在看这本书之前,我属于勤奋的人,而看完这本书以后,我要努力变成懒惰的人。
不要在去庞大的开始菜单里面一项一项搜索自己的应用程序,也不要在自己的桌面上放置眼花缭乱的快捷图标
- Eclipse简单有用的配置
dcj3sjt126com
eclipse
1、显示行号 Window -- Prefences -- General -- Editors -- Text Editors -- show line numbers
2、代码提示字符 Window ->Perferences,并依次展开 Java -> Editor -> Content Assist,最下面一栏 auto-Activation
- 在tomcat上面安装solr4.8.0全过程
eksliang
Solrsolr4.0后的版本安装solr4.8.0安装
转载请出自出处:
http://eksliang.iteye.com/blog/2096478
首先solr是一个基于java的web的应用,所以安装solr之前必须先安装JDK和tomcat,我这里就先省略安装tomcat和jdk了
第一步:当然是下载去官网上下载最新的solr版本,下载地址
- Android APP通用型拒绝服务、漏洞分析报告
gg163
漏洞androidAPP分析
点评:记得曾经有段时间很多SRC平台被刷了大量APP本地拒绝服务漏洞,移动安全团队爱内测(ineice.com)发现了一个安卓客户端的通用型拒绝服务漏洞,来看看他们的详细分析吧。
0xr0ot和Xbalien交流所有可能导致应用拒绝服务的异常类型时,发现了一处通用的本地拒绝服务漏洞。该通用型本地拒绝服务可以造成大面积的app拒绝服务。
针对序列化对象而出现的拒绝服务主要
- HoverTree项目已经实现分层
hvt
编程.netWebC#ASP.ENT
HoverTree项目已经初步实现分层,源代码已经上传到 http://hovertree.codeplex.com请到SOURCE CODE查看。在本地用SQL Server 2008 数据库测试成功。数据库和表请参考:http://keleyi.com/a/bjae/ue6stb42.htmHoverTree是一个ASP.NET 开源项目,希望对你学习ASP.NET或者C#语言有帮助,如果你对
- Google Maps API v3: Remove Markers 移除标记
天梯梦
google maps api
Simply do the following:
I. Declare a global variable:
var markersArray = [];
II. Define a function:
function clearOverlays() {
for (var i = 0; i < markersArray.length; i++ )
- jQuery选择器总结
lq38366
jquery选择器
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
- 基础数据结构和算法六:Quick sort
sunwinner
AlgorithmQuicksort
Quick sort is probably used more widely than any other. It is popular because it is not difficult to implement, works well for a variety of different kinds of input data, and is substantially faster t
- 如何让Flash不遮挡HTML div元素的技巧_HTML/Xhtml_网页制作
刘星宇
htmlWeb
今天在写一个flash广告代码的时候,因为flash自带的链接,容易被当成弹出广告,所以做了一个div层放到flash上面,这样链接都是a触发的不会被拦截,但发现flash一直处于div层上面,原来flash需要加个参数才可以。
让flash置于DIV层之下的方法,让flash不挡住飘浮层或下拉菜单,让Flash不档住浮动对象或层的关键参数:wmode=opaque。
方法如下:
- Mybatis实用Mapper SQL汇总示例
wdmcygah
sqlmysqlmybatis实用
Mybatis作为一个非常好用的持久层框架,相关资料真的是少得可怜,所幸的是官方文档还算详细。本博文主要列举一些个人感觉比较常用的场景及相应的Mapper SQL写法,希望能够对大家有所帮助。
不少持久层框架对动态SQL的支持不足,在SQL需要动态拼接时非常苦恼,而Mybatis很好地解决了这个问题,算是框架的一大亮点。对于常见的场景,例如:批量插入/更新/删除,模糊查询,多条件查询,联表查询,