(四十八)用EWMA和GARCH模型估计波动率和相关系数
ARCH、EWMA、GARCH介绍
案例
对2016年至2018年沪深300指数的涨跌幅数据建立ARCH(1)、EWMA和GARCH(1,1)三种波动率模型,并以30天前的数据为起点,逐一预测后一天的波动率。
ARCH(1)
import numpy as np
import pandas as pd
df=pd.read_excel('C:/Users/Desktop/沪深300指数.xlsx',header=0,index_col=0)
data=(df.iloc[:,0]/df.iloc[:,0].shift(1)-1).dropna()
data.name='沪深300涨跌幅'
from arch import arch_model
#建立ARCH(1)模型
arch=arch_model(y=data,mean='Constant',lags=0,vol='ARCH',p=1,o=0,q=0,dist='normal')
#vol参数可选波动率模型的类型,除了ARCH、GARCH外还有EGARCH、FIARCH、HARCH等
archmodel=arch.fit()
archmodel.summary()
archmodel.plot()
Out[6]:
<class 'statsmodels.iolib.summary.Summary'>
"""
Constant Mean - ARCH Model Results
==============================================================================
Dep. Variable: 沪深300涨跌幅 R-squared: -0.000
Mean Model: Constant Mean Adj. R-squared: -0.000
Vol Model: ARCH Log-Likelihood: 2232.59
Distribution: Normal AIC: -4459.18
Method: Maximum Likelihood BIC: -4445.41
No. Observations: 730
Date: Sun, Mar 29 2020 Df Residuals: 727
Time: 18:59:32 Df Model: 3
Mean Model
==============================================================================
coef std err t P>|t| 95.0% Conf. Int.
------------------------------------------------------------------------------
mu -3.0768e-04 4.190e-04 -0.734 0.463 [-1.129e-03,5.135e-04]
Volatility Model
============================================================================
coef std err t P>|t| 95.0% Conf. Int.
----------------------------------------------------------------------------
omega 8.9476e-05 8.234e-06 10.866 1.671e-27 [7.334e-05,1.056e-04]
alpha[1] 0.4000 0.107 3.754 1.737e-04 [ 0.191, 0.609]
============================================================================
Covariance estimator: robust
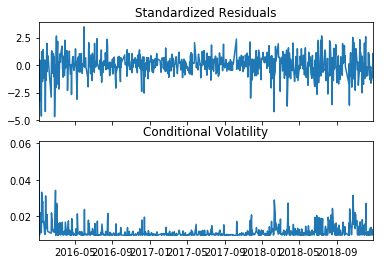
可以看到ARCH(1)模型的参数ω=0.0000895,α=0.4,因此模型表达式为σn2=0.0000895+0.4(un-1)2。
GARCH(1,1)
#建立GARCH(1,1)模型
garch=arch_model(y=data,mean='Constant',lags=0,vol='GARCH',p=1,o=0,q=1,dist='normal')
garchmodel=garch.fit()
garchmodel.params
Out[7]:
mu 0.000465
omega 0.000003
alpha[1] 0.100000
beta[1] 0.880000
Name: params, dtype: float64
garchmodel.plot()
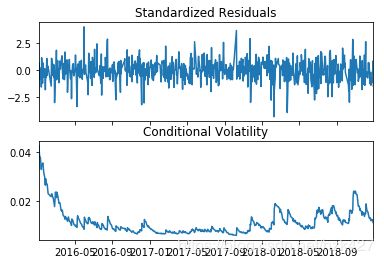
可以看到GARCH(1,1)模型的参数ω=0.00000298,α=0.1,β=0.88,因此模型表达式为σn2=0.00000298+0.1(un-1)2+0.88(σn-1)2。下面计算长期波动率,即√VL:
vol=np.sqrt(garchmodel.params[1]/(1-garchmodel.params[2]-garchmodel.params[3]))
vol
Out[10]: 0.012212037954677738
EWMA
由于实践证明对于日收益率数据,λ=0.94时预测效果最好,因此EWMA模型为σn2=0.06(un-1)2+0.94(σn-1)2。
逐一预测后30天的波动率并比较
根据上述三种模型的结果,我们就可以根据前一天的波动率和收益率数据来预测下一天的波动率。最后30天数据日期为2018年11月19号-2018年12月28号,因此随着每一天的数据更新,我们可以用以上三种模型预测2018年11月20号-2018年12月29号的波动率数据,并画图比较:
#ARCH(1)
vol301=np.zeros(30)
u30=data[-30:]
vol301[0]=np.sqrt(0.0000895+0.4*data[-31]**2)
for i in range(29):
vol301[i+1]=np.sqrt(0.0000895+0.4*u30[i]**2)
#GARCH(1,1)
vol302=np.zeros(30)
vol302[0]=data[-34:-29].std()#5日MA估计11月19号的波动率
for i in range(29):
vol302[i+1]=np.sqrt(0.00000298+0.1*u30[i]**2+0.88*vol302[i]**2)
#EWMA,λ=0.94
vol303=np.zeros(30)
vol303[0]=data[-34:-29].std()
for i in range(29):
vol303[i+1]=np.sqrt(0.06*u30[i]**2+0.94*vol302[i]**2)
#画出30天的波动率预测图
import datetime
riqi=(u30.index+datetime.timedelta(days=1)).strftime("%Y-%m-%d")
import matplotlib.pyplot as plt
plt.figure(figsize=(15,5))
plt.plot(riqi,vol301,label='ARCH(1)')
plt.plot(riqi,vol302,label='GARCH(1,1)')
plt.plot(riqi,vol303,label='EWMA')
plt.xticks(rotation=30)
plt.legend()
plt.grid()
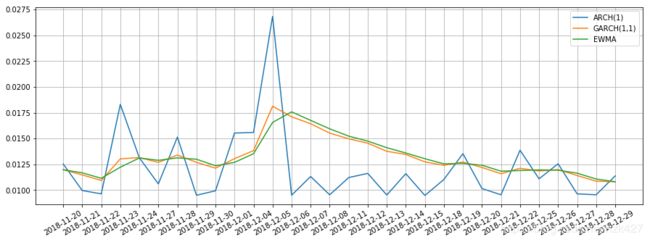
可以发现GARCH(1,1)和EWMA模型的预测结果是非常相似的。
EWMA和GARCH估计相关系数
思路和估计波动率一样,方差换成了协方差,u²n-1换成了ux n-1· uy n-1:

注意上式中Covn-1 = ρxy,n-1×σx,n-1×σy,n-1,后面三项都可以通过同一种方法估算出来,比如5日MA。计算出Covn后代入相关系数公式可得ρxy,n = Covn / σx,n×σy,n。下面简单介绍相关系数5日MA的计算方法:
df2=pd.read_excel('C:/Users/Desktop/沪深300指数与上证180指数的日涨跌幅.xlsx',header=0,index_col=0)
cor=df2.rolling(window=5).corr().dropna();cor
Out[16]:
沪深300涨跌幅 上证180涨跌幅
日期
2016-01-08 沪深300涨跌幅 1.000000 0.999923
上证180涨跌幅 0.999923 1.000000
2016-01-11 沪深300涨跌幅 1.000000 0.999783
上证180涨跌幅 0.999783 1.000000
2016-01-12 沪深300涨跌幅 1.000000 0.999685
... ...
2018-12-26 上证180涨跌幅 0.966159 1.000000
2018-12-27 沪深300涨跌幅 1.000000 0.984355
上证180涨跌幅 0.984355 1.000000
2018-12-28 沪深300涨跌幅 1.000000 0.987533
上证180涨跌幅 0.987533 1.000000
[1454 rows x 2 columns]
c=cor.loc[(slice(None),'沪深300涨跌幅'),:]
d=pd.Series(c.iloc[:,1].values,index=df2.index[4:],name='5日移动平均相关系数')
d.index.name='date'
d.plot()
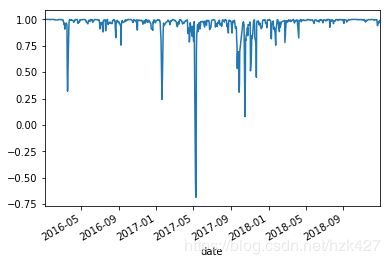
其中cor.loc[(slice(None),‘沪深300涨跌幅’),:]的各参数的解释如下:loc[(a,b),c]中第一个参数元组为索引内容,a为level0索引对应的内容,b为level1索引对应的内容;因为cor是一个dataframe,所以要用c即‘:’来指定任意的列;slice(None)是切片操作,这里用来选择任意的level0索引,也就是日期。

