大家好,距离上一篇博文将近一个月,时间过得好快,原本计划周更的,后面推到半月跟,实际到现在是月更,每次在准备写点什么的时候,都会被一些杂乱的事物打扰,哎,重度拖延症、懒癌晚期~
继上次述说了《计算机结构与组成》的课后作业之后,这次我来说说《计算机图形学》的课后作业吧(ps:上课内容都差不多,课后作业比较有意思)
《计算机图形学》是我大三上学期的专业选修课,课程没有特别的教材,教学使用的PPT和课后作业是MIT大学的图形学内容:http://groups.csail.mit.edu/graphics/classes/6.837/F04/calendar.html 这是很老的一个版本了,看链接还是04年的,现在MIT已经将这门课作为公开课开放给全世界的同学学习,课程代号是6.837,给一个该课程历年信息:http://stellar.mit.edu/courseguide/course/6/fa17/6.837/index.html 有需要可以自己在里面搜索哦~~~
我们还是继续说这门课的课后作业吧。《计算机图形学》的课后作业分几个大模块,或者说是方向。有点线面、光线投射、迭代系统、粒子系统等等(其实是我自己划分的)。由于作业量多,我就分几次来细说,这次我先说说点线面这一块的内容吧(没有点,作业中没涉及到点的内容,点本身也没啥好说的)。
首先来说说曲线和曲面。在做这个作业之前,原作者已经把基础框架、绘制的方式、点选操作等等都实现好了,我们只需要按照作者的设计和模板完成曲线曲面的计算,也就是作者已经定好框架和接口,我们只用实现曲线的计算(是不是很方便)
对于图形学中的基本点线面中的点,没啥好说的,直线好像也没啥要弄的,毕竟已经读到大学,这些基本的认识还是有的。那就先来认识一下在图形学中用得比较多的特殊曲线。
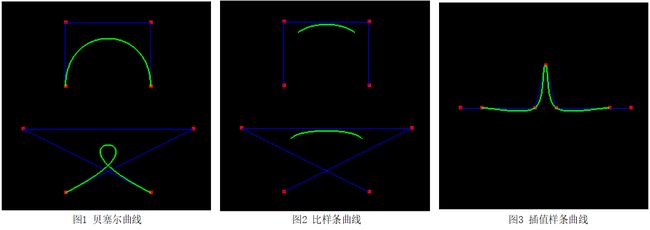
如上图所示,在曲线方面,先学习贝塞尔曲线、比样条曲线和插值样条曲线。在上面的三种曲线中,贝塞尔曲线算是工作后见到和用到得比较多曲线,比如角色动画里的动画曲线、各种插值曲线等等,用贝塞尔曲线都能得到比较好的控制效果。
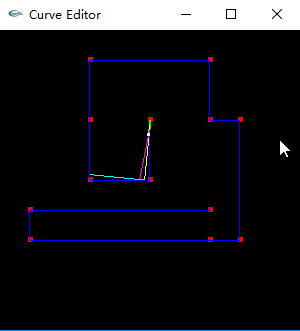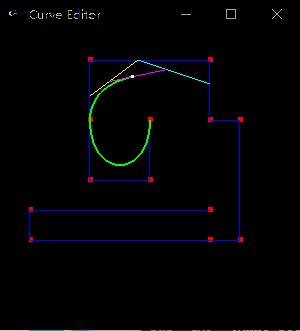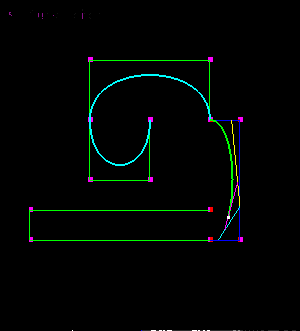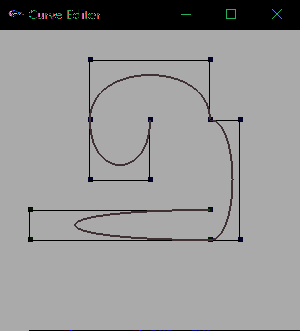
在完成基本的曲线绘制计算后,作为附加作业,提出了使用几何办法来绘制贝塞尔曲线,并用动图来展现贝塞尔曲线的计算和绘制过程,结果如下图所示:
嗯,这里提到的贝塞尔的几何算法,可以非常好的理解贝塞尔曲线,同时在工作后如果忘记了贝塞尔的计算方程,常常用这种几何算法来解燃眉之急,嘿嘿~~~(ps:几何算法在未加优化和变形的时候,效率不是最高的)
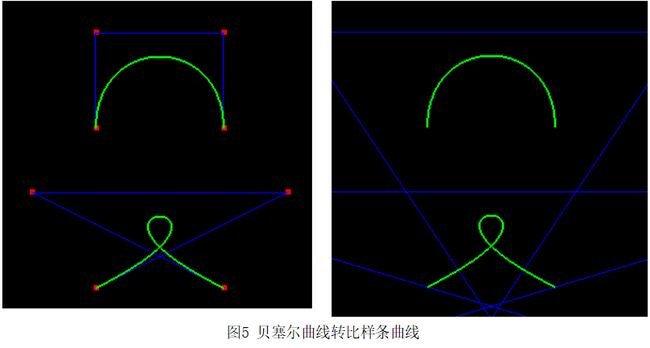
完成曲线的基本计算后,开始研究曲线间的转换,目前只完成了贝塞尔曲线和比样条曲线间的互相转换,如下所示:
这个是贝塞尔曲线转比样条曲线,可以看到画出的图像完全一样,但是曲线的控制点却天差地别。
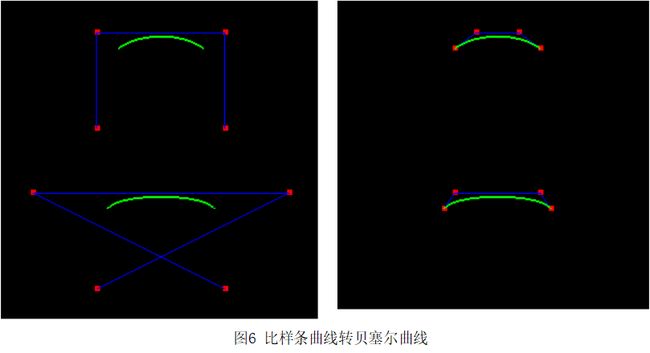
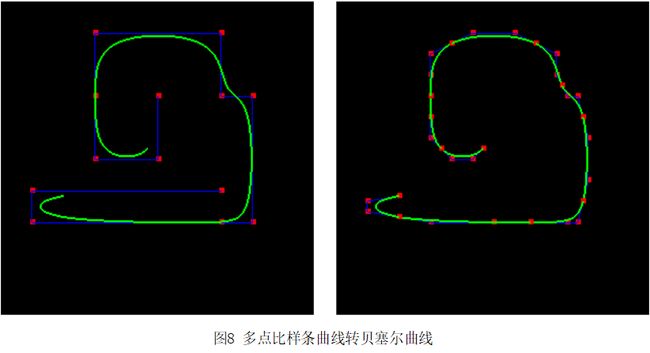
这是比样条曲线转贝塞尔曲线,左边是前面绘制的比样条曲线,右边是该比样条曲线转换为贝塞尔曲线的结果。
在上面完成了4个控制点的曲线后,我们再来玩玩多余四个控制点的
ps:多个控制点有多种不同处理的方式
- 每四个控制点组成一个小的曲线,然后连接在一起,这种多控制点曲线其实是一小段一小段的曲线连接起来的,会出现比较突兀的连接点,也就是切线不平滑(这种最简单)
- 用所有的控制点一起作用生成一条平滑曲线
第一种比较简单,采用的也比较多
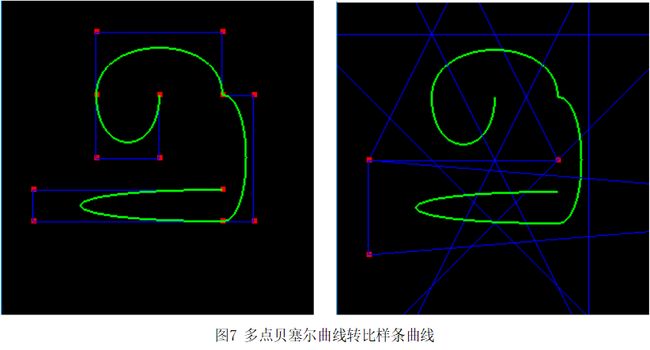
图就看下面的吧。有多余四个点的曲线,自然有多余四个点的曲线间的转化,如下所示:
左边是多余4个点(3n+1) 的贝塞尔曲线,右边是该曲线转化为比样条曲线的图形。
左边是多点(3n+1) 控制的比样条曲线,右边是该曲线转化的贝塞尔曲线
在曲线玩得差不多后,我们就该进阶了,该开始玩玩简单的面了,就以前的知识,我们知道:点运动生成线,线运动生成面,所以最先接触的面则是有上面提到的曲线来生成。曲线中最易控制和使用的是贝塞尔曲线,所以就有了下面的图形:
- 首先是由6个点(实际有7个)组成一个圆环,如下图左边所示
- 然后通过这个圆环旋转360度,生成一个圆环体,如下图中间所示
- 最后控制圆环的采样精度和旋转360度中的采样精度,可以生成不同精度的圆环体,如下图右边所示
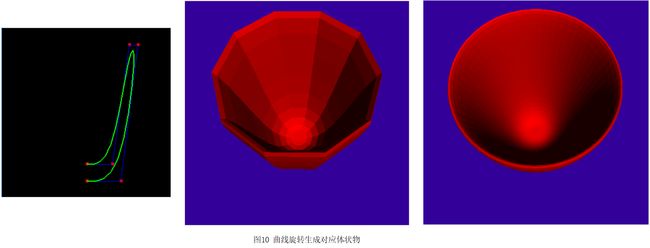
除了圆环体,我们还可以通过控制曲线旋转生成不同的体状物体,如下所示:
这是一个通过曲线生成圆桶状的物体。
玩了曲线,也玩了由曲线旋转生成的面,接下来我们来玩玩由多条曲线插值生成的曲面,如下所示:
这里是由4条贝塞尔曲线并列后,生成的贝塞尔曲面:
- 首先取到4条贝塞尔曲线上相同等分的4个点
- 然后由这4个点生成一条贝塞尔曲线
- 在生成贝塞尔曲线上等分相同的点记录下来
- 把得到的点按相同规则缠绕生成三角形面,然后显示出来
图最左边是相应的贝塞尔控制点,后面三张是不同采样精度得出的贝塞尔曲面
你以为生成了最终的贝塞尔曲面就是这次作业的终极目标么?其实不是的,这个作业的终极目标是由上面完成的功能,同时运行生成一个没有底的茶壶,如下所示:
如果全部都按要求做了,那么这里什么都不用做就可以看到最终的茶壶效果
这里是茶壶的3D查看效果,这个茶壶是没有底的,如果有底的话,那就是你做错了O(∩_∩)O哈哈~