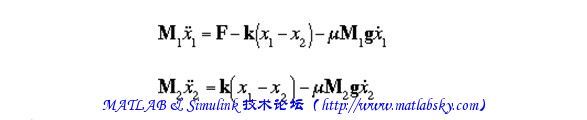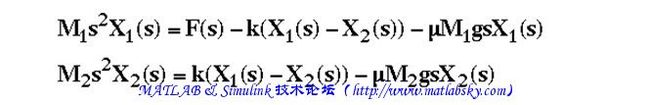MATLAB与自动控制系列教程一: MATLAB建模
首先对说明一下,原版内容在这片之前有一个简单的基础内容,我用MATLAB 入门教程目录9个部分进行了完善,当然还需要很多改进的地方,就像这个教程一样,我在前面选折的主题分类就是讨论,希望通过大家的指正在2~3变翻新以后能成为一个经典的教程,届时会推出视频教程。希望和大家一起分享一起进步!!
MATLAB建模
MATLAB可以用来表示一个物理系统或模型。在本教程中,您将学习如何把微分方程式输入到MATLAB。让我们先来复习一下如何用微分方程式表示一个物理系统。
火车系统
在这个例子中,我们会考虑一个玩具火车的机头和一节车厢。假设该列车只往一个方向行驶,我们想控制的火车,使其以一个恒定速度稳启动和停止。
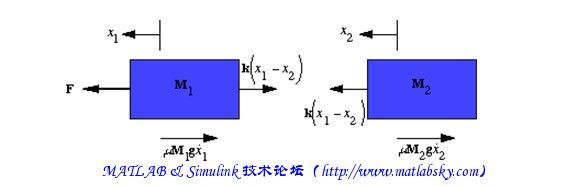
机头的质量和车厢的质量将用M1和M2代表。两者用一个弹簧链接起来了,它具有刚度系数K。F代表由发动机的引力,希腊字母mu(这也将是由字母U代表),代表了滚动摩擦系数。
自由受力图和牛顿定律
分析该系统可以得出以下自由受力图。
从牛顿定律你可以得出,在一个系统的作用力之和等于质量乘以它的加速度。在这种情况下,对M1的作用力有弹簧力,发动机的引力和摩擦力等作用。在M2的作用力为弹簧力和摩擦力。在垂直方向上,压力与支持力相等,使不会在垂直方向的加速度。
在水平方向的运动方程如下:
状态变量和输出方程
这种系统方程组可以写成状态变量的形式(state-variable form)。状态变量的位移用X1和X2代表,速度用V1和V2代表,输入量用F表示。那么状态变量方程将如下所示:
假如系统的输出用发动机的速度表示,输出方程为:
进入下一个内容之前让我稍微铺垫一下。
拉普拉斯变换与逆变换
拉普拉斯同志在天堂一定笑的很开心,因为有了MATLAB,呵呵,关于L变换和逆变换,只要两个函数就可以搞定,laplace和ilaplace。这两个函数是符号计算工具箱里的函数。
简单介绍一下拉普拉斯变换。为什么需要拉普拉斯变换,其实用语言表达出来得说一大堆。用简单的例子说明一下。
如果给你上面俩个式子让你解,哪个更容易解呢??
当然是式子2啦!!但是你要知道他们表达要求的解是一样的,只不过第一个求解相当的麻烦,但是第二个就像你看到的那么简单,是不是一下就找到结了呢??(但是第二个解完要变回去哦~~)
下面是拉普拉斯的定义,为什么这么定义,估计除了他本人应该没有人知道。但是神奇的是这么定义之后工程领域大所数的微分方程就变成上面例子里的第2个式子一样变得简单了。所以说学好微积分将来您也可能创出像jinxuejun变换的定义呢??
想了解更具体的那就去看书吧。一般情况下,L变换是以字母t为自变量,以其他字母作为参数来进行变换。记得我们前面说的,必须告诉MATLAB,这些东西统统都是字符变量,才可以进行下面的计算。
理论简述:
首先,告诫大家不要学着学着就忘本了。
现在我来问你们几个问题,如果你能回答上来,说明你还没有忘本。如果对下面的问题不是特别的清楚,建议你最好先弄清楚再往下看。
第一:以连续系统为例子,传递函数是怎么来的。
第二:为什么要用传递函数来表达系统,好处在哪里,有什么局限。
OK,我来给大家的一个简单的参考答案,连续系统中,把一个系统的微分方程等号两边分别取拉普拉斯变换,然后把输入和输出放在一边,其他项放在另一边就得到了我们的传递函数模型。
实际上,通过L变换,系统的微分方程模型转换成了代数方程模型,分析代数方程无论从难度和手段的多样性都要比直接分析微分方程好很多,因此,我们采用传递函数来研究一个系统更加的直观和方便。另外,传递函数表达了一个系统输入和输出的关系,也就是说,一旦系统给定了,那么它的传递函数就不会变化,也就是说传递函数不受输入和输出的变化影响。
传递函数的局限在于,它只能反映系统的外部特性,也就是输入和输出的特性,因此,传递函数模型也被一些人称为“黑箱”模型,因为我们只能看到由它引起的外部变化,并不能解决系统内部的一些问题和矛盾。要解决这个问题就要用状态空间模型和现代控制理论,因此,状态空间模型又称“白箱”模型,我们可以清晰的看到它的内部结构,以便对系统进行优化和完善。
1. 传递函数
要找到系统的传递函数,我们首先采取的微分方程的Laplace变换。
输出为Y(s)=V2(s)=s X2(s)。消掉变量X1得到表达式Y(s)/F(s)。如果要得到传递函数,初始条件必须给定。传递函数看起来应该如下所示的一个。
2. 状态空间(State-space)
另一种解法是使用的状态空间形式。四个矩阵A,B,C和D表示系统的状态,将被用来解决这个问题。状态空间形式可以从状态变量得出,输出方程如下所示。
MATLAB再现
现在我们将告诉你如何用MALTAB在m文件里把上面介绍的方程式表达出来。由于MATLAB不能计算的符号值,让我们把数值分配到每个符号。如下
· M1 = 1 kg
· M2 = 0.5 kg
· k = 1 N/m
· F= 1 N
· u = 0.002 sec/m
· g = 9.8 m/s^2
创建一个新的M-文件,输入以下命令。
- M1=1;
- M2=0.5;
- k=1;
- F=1;
- u=0.002;
- g=9.8;
现在你有两个选择:1)使用传递函数,或2)使用状态空间形式来解决这个问题。如果您选择使用的传递函数,把下面的命令添加到的M -文件,应该贴在您刚才创建的末尾加入以下命令。
- num=[M2 M2*u*g 1];
- den=[M1*M2 2*M1*M2*u*g M1*k+M1*M2*u*u*g*g+M2*k M1*k*u*g+M2*k*u*g];
- train=tf(num,den)
如果您选择使用状态空间的形式,把下面的命令添加到的M -文件,应该贴在您刚才创建的末尾加入以下命令,注意千万不要贴上卖命令再贴这个命令。选折俩个中的一个,如果想试验这个结果再新建一个m文件重新输入便是。
- A=[ 0 1 0 0;
- -k/M1 -u*g k/M1 0;
- 0 0 0 1;
- k/M2 0 -k/M2 -u*g];
- B=[ 0;
- 1/M1;
- 0;
- 0];
- C=[0 1 0 0];
- D=[0];
- train=ss(A,B,C,D)
如果想了解更多的关于矩阵的知识请看MATLAB 入门教程目录。
继续解决问题
一旦微分方程系统模型输入到MATLAB问题已经转换到传递函数或状态空间形式,需要利用开环和闭环系统的理论进行研究。这个将是下面需要学习的内容。
大部分操作可以通过使用传递函数或状态空间模型来表达。此外,它的方法很简单,如果必须用别的方法来表达。你需要学习如何从一个转换到其他形式,可以到下面给出的链接参考学习一下。