Randomized SVD大法好！

Truncated SVD

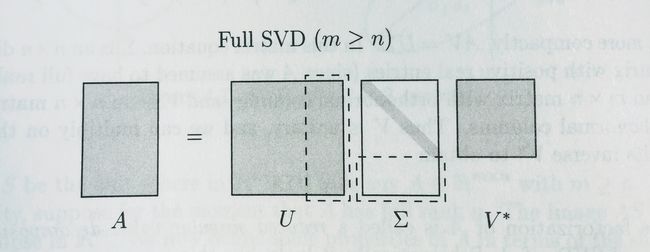
full_svd的full在于 U U 和 V V 都是方阵，而 U U 中被虚线框出的部分的重要性都为0，对 A A 其实是没有贡献的。

Reduced SVD和Truncated SVD是不同的，Truncated SVD是去掉最末尾的几个singular value来近似原矩阵。

而Reduced SVD就是把多余的bottom去掉，对应的 V V ​ 仍然是方阵。

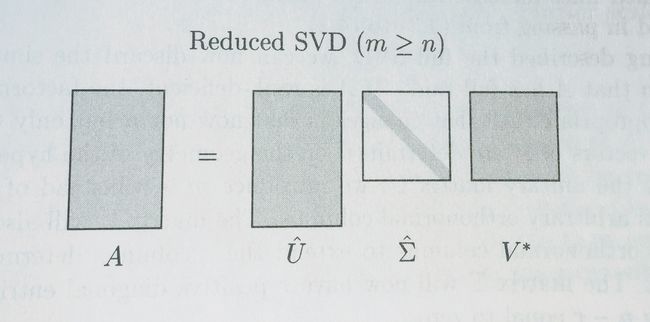
如果我们要得到Truncated SVD，一种方法是先做Full SVD，再cut off 一些columns。但是Full SVD is slow. This is the calculation we did above using Scipy’s Linalg SVD:

# 32s
%time U, s, Vh = linalg.svd(vectors, full_matrices=False)

Fortunately, there is a faster way：只要5个eigenvalue

# 4.92s
%time u, s, v = decomposition.randomized_svd(vectors, 5)

# ((2034, 5), (5,), (5, 26576))
u.shape, s.shape, v.shape

SVD复杂度分析

The runtime complexity for SVD is O(min(m2n,mn2)) O ( min ( m 2 n , m n 2 ) )

How to speed up SVD?

Idea: Let’s use a smaller matrix (with smaller n n )!

Instead of calculating the SVD on our full matrix A A which is m×n m × n , let’s use B=AQ B = A Q , which is just m×r m × r and r<<n r << n

B B 这个矩阵又高又瘦，相当于把 A A 的一部分column都cut off掉了。所谓的approximate是指， A A 的columns和 B B 的columns可以span出一个similar的space。这样就可以用fewer columns span出一个一样的space。

We haven’t found a better general SVD method, we are just using the method we have on a smaller matrix.

Implement Randomized SVD

A≈QQTA A ≈ Q Q T A

1. Compute an approximation to the range of A A . Note that the range of A A is Range(A)={y:Ax=y} R a n g e ( A ) = { y : A x = y } , or A A 的columns的 span（Linear Combination）。

   直观点说就是，把 A A 视为一个变换矩阵，将vector x x 变换为 y y ，而 y y 组成的范围就是 A A 的 range。所以在后面的代码中用了一个for循环不停 A@Q A @ Q ，就是希望最后求出的 Q Q 能够和 A A 有similar column space but fewer columns。

   That is, we want Q Q with r r orthonormal columns such that

   A≈QQTA A ≈ Q Q T A

   【注意】如果 Q Q 是orthogonal matrix（行列均为orthonormal），则有 QQT=I Q Q T = I 。但是这里 Q Q 只有column是orthonormal的，所以是approximate I I 。

2. Construct B=QTA B = Q T A , which is small ( r×n r × n )。 A:m×n A : m × n , Q:m×r Q : m × r ，所以 B B 是 r×n r × n << m×n m × n

3. Compute the SVD of B B by standard methods (fast since B B is smaller than A A ), B=SΣVT B = S Σ V T

4. Since

   A≈QQTA=Q(SΣVT) A ≈ Q Q T A = Q ( S Σ V T )
   if we set U=QS U = Q S , then we have a low rank approximation A≈UΣVT A ≈ U Σ V T . 这样就得到了 A A 的SVD分解式，并且是lower rank的！

【注意】 U U 的column必须是orthonormal的，才符合SVD的要求， U=QS U = Q S 可以说明 U U 是orthonormal的吗？
可以滴，因为 S S 和 Q Q 都是column orthonormal的。 (QS)TQS ( Q S ) T Q S

How to find Q Q

使用随机采样方式构建矩阵 Q Q ：

• 1.构建一个 n∗(k+p) n ∗ ( k + p ) 维的高斯随机矩阵 Ω Ω
• 2.进行矩阵乘积运算 Y=AΩ Y = A Ω
• 3.利用QR分解获得 Y Y 的正交基 Q=qr(Y) Q = q r ( Y )

To estimate the range of A A , we can just take a bunch of random vectors wi w i , evaluate the subspace formed by Awi A w i . We can form a matrix W W with the wi w i as it’s columns. Now, we take the QR decomposition of AW=QR A W = Q R , then the columns of Q Q form an orthonormal basis for AW A W (like ei,ej,ek e i , e j , e k ), and AW A W gives us the range of A A . （因为 A A 乘上了一堆随机的vector wi w i ，相当于把这些 wi w i 变换为其他vector，这些vector合并到一起基本上就可以看做是 A A 的range了）

And R R is a upper trianglur matrix.

Since the matrix AW A W of the product has far more rows than columns and therefore, approximately, orthonormal columns. This is simple probability - with lots of rows, and few columns, it’s unlikely that the columns are linearly dependent.

The method randomized_range_finder finds an orthonomal matrix whose range approximates the range of A A (step 1 in our algorithm above). To do so, we use the LU and QR factorizations:

# computes on orthonormal matrix whose range approximates the range of A
# power_iteration_normalizer can be safe_sparse_dot (fast but unstable)
def randomized_range_finder(A, size, n_iter=5):
    Q = np.random.normal(size=(A.shape[1], size))

    # 这里不停 A @ Q ，是为了使Q最大化接近A的range，回想之前所说的A的range是矩阵A对vector做变换后的范围
    # 然后对 A @ Q做LU分解是因为：一直乘一个相同的数是unstable的（expose/0），做LU类似一种Normalize（为啥？）
    for i in range(n_iter):
        Q, _ = linalg.lu(A @ Q, permute_l=True)
        Q, _ = linalg.lu(A.T @ Q, permute_l=True)

    Q, _ = linalg.qr(A @ Q, mode='economic')
    return Q

How to choose R R

Suppose our matrix has 100 columns, and we want 5 columns in U U and V. To be safe, we should project our matrix onto an orthogonal basis with a few more rows and columns than 5 (let’s use 15). At the end, we will just grab the first 5 columns of U U and V V .

So even although our projection was only approximate, by making it a bit bigger than we need, we can make up for the loss of accuracy (since we’re only taking a subset later).

Implement

And here’s our randomized SVD method:

• 4.构建低维矩阵 B=QTA B = Q T A , 维度为(k+p)

• 5.矩阵 B B 的SVD分解， [Û ,ΣB,VB]=SVD(B) [ U ^ , Σ B , V B ] = S V D ( B )

• 6.用 Q Q 更新左奇异向量， UB=QÛ  U B = Q U ^ ，也就是前面提的 U=QS U = Q S
• 7.得到最终结果 UA=UB(:,1:k) U A = U B ( : , 1 : k ) , ΣA=ΣB(1:k,1:k) Σ A = Σ B ( 1 : k , 1 : k ) , VA=VB(:,1:k) V A = V B ( : , 1 : k )

def randomized_svd(M, n_components, n_oversamples=10, n_iter=4):
    # `n_components`代表我们想要的前n个singular value，也就是topic model中的topics
    n_random = n_components + n_oversamples

    Q = randomized_range_finder(M, n_random, n_iter)

    # project M to the (k+p) dims space using the basic vectors
    B = Q.T @ M

    # compute the SVD on the thin matrix: (k+p) wide
    Uhat, s, V = linalg.svd(B, full_matrices=False)
    del B
    U = Q @ Uhat

    return U[:, :n_components], s[:n_components], v[:n_components, :]

Q：为什么要用 n_oversamples？

如果我们只想要5个topic，但是在计算时要取得稍稍多一点，比如15个topics。n_oversamples is kind of like a safety buffer，因为我们对这堆documents到底该归为几个topic是一无所知的。你如果只取5个topic的话，可能有一些不属于这些topic的document会被squeeze into those 5 topic。但是你取15个topic的话，那这前5个topic里面的document就会clean许多。

# 137ms
%time u, s, v = randomized_svd(vectors, 5)

#((2034, 5), (5,), (5, 26576))
u.shape, s.shape, v.shape

Plot Error

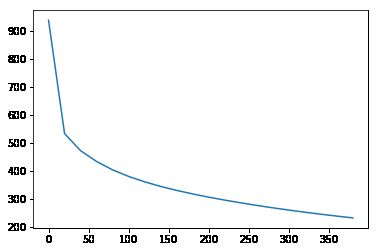
Calculate the error of the decomposition as we vary the # of topics, 然后plot一下result：

step = 20
n = 20
error = np.zeros(n)

for i in range(n):
    U, s, V = randomized_svd(vectors, i*step)
    reconstructed = U @ np.diag(s) @ V
    error[i] = np.linalg.norm(vectors - reconstructed)

plt.plot(range(0,n*step,step), error)

根据上图可以看出，前几个singular value capture more than additional singular value.

Randomized SVD in sklearn

%time u, s, v = decomposition.randomized_svd(vectors, 5)

%time u, s, v = decomposition.randomized_svd(vectors.todense(), 5)

Background Removel with Randomized SVD

采用经典的 BMC 2012 Background Models Challenge Dataset 数据集。

An image from 1 moment in time is 60 pixels by 80 pixels (when scaled). We can unroll that picture into a single tall column. So instead of having a 2D picture that is 60×80 60 × 80 , we have a 1×4,800 1 × 4 , 800 column

This isn’t very human-readable, but it’s handy because it lets us stack the images from different times on top of one another, to put a video all into 1 matrix. If we took the video image every tenth of a second for 113 seconds (so 11,300 different images, each from a different point in time), we’d have a 11300×4800 11300 × 4800 matrix, representing the video!

如下图是uroll and stack之后的矩阵 M M (4800, 11300)，4800是一帧图片（60x80）拉长后的向量长度，11300是帧数。图中的solid横线代表background；wave代表行人的moving；column代表 a moment in time。原矩阵 M M 每一列都是某时间点上一帧图像拉长后形成的vector。

​ Randomized SVD背景分离

若做rank=2的SVD decomposition：

from sklearn import decomposition

# rank=2
u, s, v = decomposition.randomized_svd(M, 2)

# ((4800, 2), (2,), (2, 11300))
u.shape, s.shape, v.shape

# low_rank.shape: (4800, 11300)
low_rank = u @ np.diag(s) @ v

plt.figure(figsize=(12, 12))
plt.imshow(low_rank, cmap='gray')

根据上图可以看出来rank=2时，capture的几乎都是background，因此原矩阵和low_rank的差就是运动的人。

rank=2，只关注最大的2个奇异值，它们只会capture最主要的信息（背景），所以reconstruct后得到的就是背景矩阵。

plt.imshow(np.reshape(low_rank[:,140], dims), cmap='gray');

plt.imshow(np.reshape(M[:,140] - low_rank[:,140], dims), cmap='gray')

若做rank=1的Randomized SVD，分离效果会更好。