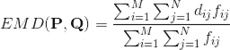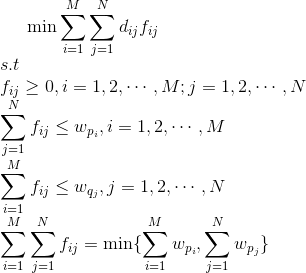图像检索中的相似度度量:EMD距离(Earth Mover's Distance)
EMD距离即Earth Mover's Distance,是由2000年IJCV期刊文章《The Earth Mover's Distance as a Metric for Image Retrieval》提出的一种图像相似度度量方法,从文章标题也可以得知,最初EMD的概念是用于图像检索的。后来因为其各种优点,逐渐用到其他方面的相似度度量。这篇文章主要理解EMD的概念。
signature
论文定义,“We introduce a distance between two signatures that we call the Earth Mover's Distance(EMD)”,那么这里的signature是什么呢?
1.图像的直方图就是把全部像素值量化为一系列bin,统计每个bin的像素个数;bin值可以看作特征,bin高度可以看作该特征的重要程度。
2.而 signature 定义为一系列的重要特征,可以写作 s = (m, w),m是某个特征,w是该特征的权重。文中说“A signature is a set of the main clusters or modes of a distribution”,作者认为,传统的完整直方图一般会聚集在某些bin上,这样过于浪费空间,用 signature 可以较稀疏的表达直方图内容。
事实上,虽然原文章是由 histogram 引出 signature 及 EMD 的定义,但实际用于计算EMD时,因为不同情况的使用方式不同,只要是符合要求的特征即可。
EMD
EMD本身是一个线性规划问题。假设,
![]() ,
, ![]()
pi是一张图像的某个特征(比如bin值),wpi是特征pi的权重(比如该bin像素数量),而qj是另一张图像的某特征,wqj是特征qj的权重。
另外定义一个特征p集合和特征q集合之间的距离矩阵 [dij],每一项dij代表pi和qj的距离(比如L1、L2距离等),可知 [dij] 是个 MxN 矩阵。
问题,
希望找到一个flow,它也是一个矩阵 F = [fij] ,每一项fij代表从pi到qj的流动数量,dij是pi位置到qj位置的代价(距离),从而最小化全局的代价函数:
这个流动量就是线性规划的解,而 EMD的定义 就是这个代价函数再作归一化后的表达,即再除以对fij的求和。
写成数学形式:(有四个约束条件)
然后来通俗点理解EMD的本质:
Earth Move翻译过来是搬土,指把P位置的m个坑的土,用最小的代价搬到Q位置的n个坑中,dij是pi到qj两个坑的距离,fij是从pi搬到qj的土量,则WORK工作量就是要最小化的目标。线性规划求解出fij后,再用fij对WORK作个归一化,就得到了EMD。
那么问题来了,为什么要用这个运输问题来定义 EMD 呢?
论文给的解释是,"Signature matching can be naturally cast as a transportation problem by de fining one signature as the supplier and the other as the consumer, and by setting the cost for a supplier-consumer pair to equal the ground distance between an element in the fi rst signature and an element in the second."
这意味着,在求解出最优运输方案 [fij] 时,同时也找到了两边最匹配的signature,如此一来计算的distance是合理的,所以EMD图像相似度匹配是有效的。
原运输问题
有助于理解那四个限制条件,这里转自别人翻译的结果。
引用:http://www.sigvc.org/bbs/forum.php?mod=viewthread&tid=981
原文:http://d.hatena.ne.jp/aidiary/20120804/1344058475
C语言使用EMD举例
这个例子是EMD提出者Rubner在其公开的C语言代码中提到的,编译依赖emd.c和emd.h。其中特征量类型 feature_t 在 emd.h 中定义如下:
typedef struct { int X, Y, Z; } feature_t;# include
# include
# include "emd.h"
/* 欧几里得距离 */
float dist(feature_t *F1, feature_t *F2) {
int dX = F1->X - F2->X;
int dY = F1->Y - F2->Y;
int dZ = F1->Z - F2->Z;
return sqrt(dXdX + dY*dY + dZ*dZ);
}
int main() {
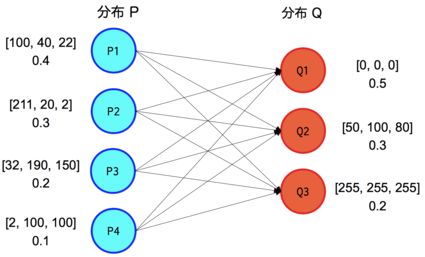
/* 分布P的特征矢量 */
feature_t f1[4] = { {100,40,22}, {211,20,2}, {32,190,150}, {2,100,100} };
/*分布Q的特征矢量 */
feature_t f2[3] = { {0,0,0}, {50,100,80}, {255,255,255} };
/*分布P的权重 */
float w1[5] = { 0.4, 0.3, 0.2, 0.1 };
/*分布Q的权重 */
float w2[3] = { 0.5, 0.3, 0.2 };
/*分布P的签名 */
signature_t s1 = { 4, f1, w1 };
/*分布Q的签名 */
signature_t s2 = { 3, f2, w2};
/* 计算EMD */
float e;
e = emd(&s1, &s2, dist, 0, 0);
printf("emd = %f\n", e); return 0;
}