概率图模型理解

本文地址：http://blog.csdn.net/ismarvellous/article/details/78828566，转载请注明出处。

今天在看《Deep Learning》时候看到了概率图模型，但上面并没有详细介绍，考虑到有很多模型其实都是概率图模型，比如贝叶斯网络、隐马尔科夫模型（HMM）、条件随机场（CRF）等等，应用还挺广泛的，于是就去学习一下到底什么是概率图模型。本文主要参考了《Pattern Recognition and Machine Learning》，如果有什么理解不到位的地方，还请大家指教。

概述

为什么会有概率图模型这个东西呢？虽然我们在概率论的课堂上学到的那些例子一般都是很简洁的公式，包含的变量也不多，但在实际应用中，我们遇到情况却可能是非常复杂的，包含的变量数量也非常大，比如在图像处理中，每个像素点都可以是一个变量，而其中的关系也是错综复杂。但是不要怕，还记得概率论中的加法准则和乘法准则吗？（不记得就去复习吧。。。）再复杂的问题也都是由这两个准则构成的。直接使用算术的方法来把这些分布分解开来存在一些困难，而概率图模型恰恰可以给出一种直观的表达，帮助我们理解并分析这些复杂问题。
既然是图模型，那我们就先来聊一聊什么是图。一个图由结点（ nodes）（也被称为端点（ vertices））和它们之间的链接（ links）（也被称为边（ edges）或弧（ arcs））组成。在概率图模型中，每个结点表示一个或一组随机变量，链接则表示这些变量之间的概率关系。概率图模型主要分为两种，一种是有向图模型（directed graphical model），也就是贝叶斯网络（ Bayesian network）。这种图模型的特点就是链接是有方向的，画出来就是带个箭头。另外一种是无向图（undirected graphical models），或者叫马尔科夫随机场（Markov random fields）。这种模型的的链接没有箭头，没有方向性质。
概念的叙述有点枯燥，我们直接来详细理解一下这两种图模型。

1. 贝叶斯网络（有向图模型）

我们首先来考虑一个非常简单的问题，三个变量 a,b,c 上的一个任意的联合分布 p(a,b,c) 。应用乘积准则，我们可以将它写为下面的形式：

p(a,b,c)=p(c|a,b)p(b|a)p(a)

于是我们就可以使用一个有向图来描述这个分解：

在这个图中，每个结点表示一个变量，每个箭头表示一个条件概率，起点是条件概率中的条件，终点是该随机变量。比如，从 a 指向 b 的箭头表示 p(b|a) ，并称 a 是 b 的父结点。注意， a 没有父结点，故没有输入的箭头，它直接对应于 p(a) 。于是联合概率分布就是图中这些结点变量所关联的概率之积。这里有一点是要注意的，本来 p(a,b,c) 是对称的，也就是变量没有顺序区分，但在我们的图模型中却是不对称的，选择不同的变量顺序会得到不同的图表示形式。

例子：多项式回归

在贝叶斯多项式拟合模型中，联合概率分布可以表示为：

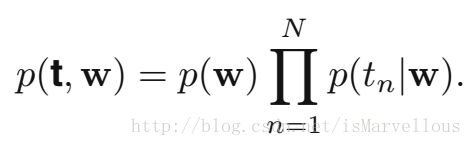
这里， t 和 w 分别表示观测变量和多项式的系数。注意，这是它们的联合概率分布，也就是说， w 也被当做一个随机变量，也就是隐变量。其对应的概率图模型如下：

这里，为了表示的简洁性，我们把所有样本 tn 放入一个方框中，称为plate。
如果我们再把模型的参数和输入显式地写出来，那就变成了这样：

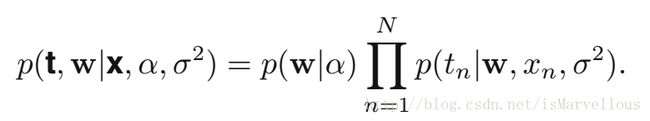
对应的概率图模型如下：

这里多了小的实心圆点来表示确定的参数。
其实我们关心的是有了这个模型，如何预测新的样本 t^ ，于是我们再把 t^ 加进来，变成下图：

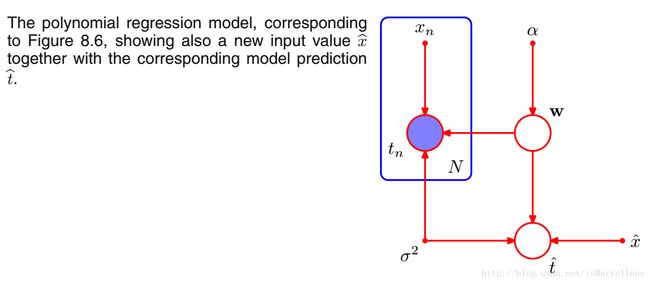
阴影结点表示该结点已被观测到（训练样本）。于是我们可以很方便地写出：

所以我们要预测的新样本 t^ 的概率分布为：

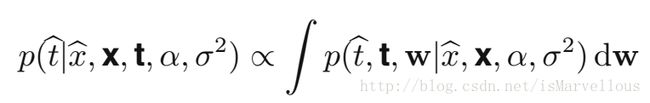
2. 条件独立性

如果有：

p(a|b,c)=p(a|c)

那么我们就说在给定 c 时 a 和 b 是 条件独立的。我们可以很容易地推出：

p(a,b|c)=p(a|b,c)p(b|c)=p(a|c)p(b|c)

关于条件独立和有向概率图的关系，我就不一一推导了，有兴趣的同学可以直接去看书中原文，写的很细，还举了例子，应该很容易理解。这里我直接给出结论，也就是 d-划分（d代表directed，有向的）：
我们考虑从A中任意结点到B中任意结点的所有可能的路径，通过路径是否被 阻隔来判断在给定C的条件下，A和B是否条件独立。具体地，如果路径满足以下任一条件，就称为被阻隔：

• 路径上的箭头以头到尾（一个是箭头的头，一个是箭头的尾）或者尾到尾（两个都是箭头的尾）的方式交汇于这个结点，且这个结点在集合C中。
• 箭头以头到头（两个都是箭头的头）的方式交汇于这个结点，且这个结点和它的所有后继都不在集合C中。
  如果所有路径都是阻隔的，那么条件独立成立。

3. 马尔科夫随机场（无向图模型）

3.1 条件独立性

从上面有向图模型和条件独立的d-划分可以发现，检测过程还是有一些繁琐的，特别是头到头的情况与其它两者不一样。而无向图模型则简化了这个检测。
无向图的链接没有方向，有链接的两个结点表示它们有某种依赖。还是对于上面的检测是否条件独立的问题，在无向图中，我们同样考虑连接集合A的结点和集合B的结点的所有可能路径。如果所有这些路径都通过了集合C中的一个或多个结点，那么所有这样的路径都被阻隔，因此条件独立性质成立。

3.2 分解性质

我们分解无向图时，把它们分解为团（clique），它是图中结点的一个子集，团中的每对结点都有链接，也就是全连接的。如下图，有五个具有两结点的团 {x1,x2},{x2,x3},{x3,x4},{x1,x3},{x1,x2} ，和两个最大团 {x1,x2,x3},{x2,x3,x4} 。
于是，我们可以将联合概率分布分解的因子定义为团块中变量的函数。记团块为 C ，将团块中的变量的集合记作 xC 。这样，联合概率分布可以写成图的最大团块的势函数（potential function） ψC(xC) 的乘积的形式：

p(x)=1Z∏CψC(xC)

这里， Z 有时被称为划分函数（partition function），是个归一化常数，等于：

Z=∑x∏CψC(xC)

势函数并不要求是具有概率意义的函数，故需要有一个划分函数对最后结果归一化，这使得无向图中势函数的选取可以更加灵活。我们要求势函数是大于等于零的，如果把势函数写为指数形式有时会更方便，即：

ψC(xC)=exp{−E(xC)}

−E(xC) 被称为能量函数，这样可以让我们把乘积变为加和。
我们下面通过一个例子来理解无向图和它的分解。

3.3 例子：图像去噪

假设我们有一个清晰二值图像 xi∈{−1,+1} ，以一定概率随机反转某些像素值，得到带噪图像 yi 。如下图：

由于噪声等级比较小，因此我们知道 xi 和 yi 之间有着强烈的相关性。我们还知道图像中相邻像素 xi 和 xj 的相关性很强。这种先验知识可以使用马尔科夫随机场模型来描述，它的无向图如下：

yi 是观测到的变量，而 xi 是要预测的变量。这个无向图反映了我们的先验： xi 只和观测 yi 以及邻近像素点有关。因此只有两种团。对于 {xi,yi} 的团，我们选择能量函数 −ηxiyi ，对于 {xi,xj} 的团，我们选择能量函数 −βxixj ，其中 η,β 都是正的常数。我们再给模型加上一个偏置项，最后得到能量函数如下：

E(x,y)=h∑ixi−β∑{i,j}xixj−η∑ixiyi

它定义了x和y上的联合概率分布，形式为：

p(x,y)=1Zexp{−E(x,y)}

我们现在固定噪声图像的像素给出的观测值 y 的元素，这个噪声图像隐式地定义了一个无噪声图像上的条件概率分布 p(x|y) 。为了恢复图像，我们希望找到一个具有较高概率（理想情况下具有最高概率）的图像x。我们使用一个简单的迭代方法，叫做迭代条件峰值（iterated conditional modes），或者称为ICM。这种想法的思想是，首先初始化变量 {xi} ，这个过程中我们只是简单地令 xi=yi （对于所有i）。然后，我们每次取一个 xj 结点，计算两个可能状态 xj=+1 和 xj=−1 的总能量，保持其他所有结点变量固定，将 xj 设置为能量较低的状态。如果 xj 不变，则概率不变，否则概率就会增大。由于只有一个变量发生改变，因此这是一个可以高效进行的简单局部计算。然后，我们对其他的结点重复更新过程，以此类推，知道满足某个合适的停止条件。结点可以用一种系统的的式更新，例如重复地依次扫描图像，或者随机地选择结点。去噪结果上面图中左下角。

总的来说，有向图和无向图都是用来描述概率分布的形式，有向图可以转化为无向图表示（从无向图转化到有向图表示不太常用）。后面有机会我们再来讨论更多的概率图模型的具体实例。