数据结构学习笔记 第三章 限定性线性表——栈和队列
文章目录
- 第三章 限定性线性表——栈和队列
- 3.1栈
- 3.1.1栈的定义
- 3.1.2栈的表示和实现
- 3.1.3栈的应用举例
- 3.2队列
- 3.2.1队列的定义
- 3.2.2队列的表示和实现
- 3.2.3队列的应用举例
- 1.打印杨辉三角
- 2.键盘输入缓冲区算法
- seqqueue.h
- main.c
- 3.3总结与提高
第三章 限定性线性表——栈和队列
- 栈和队列是两种重要的数据类型
- 特殊性:一类操作受限制的线性表,限制插入删除操作的位置
- 栈:只能在指定的一段插入和删除元素,后进先出
- 队列:在一端插入元素,另一端删除元素,先进后出,和排队一样
3.1栈
3.1.1栈的定义
- 栈作为一种限定性线性表,插入删除均在表的一端进行;
- 栈顶(Top)栈底(Bottom);
- 空栈:没有元素;
- 插入:进栈,入栈;
- 删除:出栈,退栈。
- 栈的特点:后进先出(LIFO:Last in First Out)
- ADT定义
ADT Stack {
数据元素:可以是任意类型数据,但必须为同一个数字对象。
结构关系:栈中的数据元素之间是线性关系。
基本操作:
1.InitStack(s)
操作前提:s为未初始化的栈。
操作结果:将s初始化为空栈。
2.ClearStack(s)
操作前提:栈s已存在。
操作结果:将s置为空栈。
3.IsEmpty(s)
操作前提:栈s已存在。
操作结果:判断s是否为空栈。返回TURE,FALSE。
4.IsFull(s)
操作前提:栈s已存在。
操作结果:判断栈满。返回TURE,FALSE。
5.Pish(s,x)
操作前提:栈s已存在。
操作结果:在栈顶插入元素x。若未满,则插入;若满了,报错。
6.Pop(s,x)
操作前提:栈s已存在。
操作结果:删除s顶端的元素,将其放回到x。若为空则操作失败。
7.GetTop(s,x)
操作前提:栈s已存在。
操作结果:读栈,将最顶端的元素赋值给x但不删除。
}
3.1.2栈的表示和实现
栈在计算机中有两种基本的储存结构:顺序储存结构和链式储存结构
- 顺序存储结构的栈为顺序栈
//定义一个栈,将栈和top封装在一个结构里面
#define Stack_Size 50
typdef struct
{
StackElementType elem[Stack_Size];
int top;
}SeqStack;
//初始化栈
void InitStack(SeqStack *s)
{
s->top = -1;
}
//进栈(需考虑未满)
int Push(SeqStack *S, StackElementType x)
{
if(S->top == Stack_Size - 1)
return (FALSE); //栈满
S->top++;
S->elem[S->top] = x;
return (TRUE)
}
//出栈(需考虑空)
int Pop(SeqStack *S, StackElementType *x)//x带出元素
{
if(S->top == -1)
return FALSE;//栈空
*x = S->elem[S->top];
S->top --;
return TRUE;
}
//读栈
int GetTop(SeqStack *S, StackElementType *x)
{
if(S->top == -1)
return FLASE;//空栈
else
{
*x = S->elem[S->top];
return TRUE;
}
}
- 多栈共享技术
两头往中间走。
#define M 100
typedef struct
{
StackElementType Stack[M];
int top[2]
}DqStack;
//初始化
void InitStack(DqStack *s)
{
S->top[0] = -1;
S->top[1] = M;
}
//双端进栈
int Push (DqStack *S, StackElementType x, int i)
{
if(S->top[0]+1 == S->top[1])
return FALSE;//栈满
switch(i)
{
case 0:
S->top[0]++;
S->Stack[S->top[0]] = x;
break;
case 1:
S->top[1]--;
S->Stack[S->top[1]] = x;
break;
default:
return FALSE;
}
return TRUE;
}
//出栈
int Pop(DqStack *S, StackElementType *x,int i)
{
switch(i)
{
case 0:
if(S->top[0] == -1)
return FLASE;
*x = S->Elem[S->top[0]];
S->top[0]--;
break;
case 1:
if(S->top[1] == M)
return FLASE;
*x = S->Elem[S->top[1]];
S->top[1]++;
break;
default:
return FALSE;
}
return TRUE;
}
- 链式储存的栈为链栈
typedef struct node
{
StackElementType data;
struct node *next;
}LinkStackNode;
typedef LinkStackNode *LiskStack;
void Init(LiskStack top)
{
top = malloc(sizeof(LinkStackNode));
}
int Push(LiskStack top, StackElementType x)
{
LiskStackNode *temp;
temp = malloc(sizeof (LinkStackNode));
temp->data = x;
temp->next = top->next;
top->next = temp;
return ture;
}
int Pop(LinkStack top,StackElementType *x)//先判断空栈
{
LinkStackNode *temp;
temp = top->next;
if (temp == NULL)
retrun false;
*x = temp->data;
top->next = temp->next;
free(temp);
return true;
}
对于链栈,我们可以将栈顶指针编入一个指针数组,这样就可以形成多链栈。
3.1.3栈的应用举例
- 汉诺塔问题
3.2队列
3.2.1队列的定义
- 一种限定性的线性表,一端插入元素,另一端删除元素,先进先出。
- 队尾:允许插入的一端。
- 对头:允许删除的一端。
3.2.2队列的表示和实现
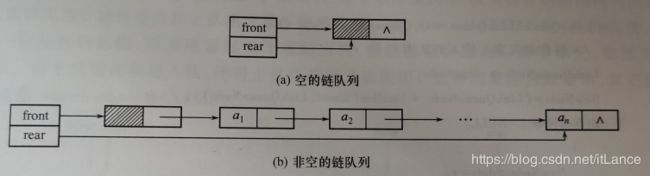
- 链队列
//定义
typedef struct Node
{
QueueElementType data;
struct Node *next;
}LinkQueueNode;
typedef struct
{
LinkQueueNode *frount;
LinkQueueNode *rear;
}LinkQueue;
//初始化
int InitQueue(LinkQueue *Q)
{
Q->front = (LinkQueueNode *)malloc(sizeof (LinkQueueNode));
if(Q->front != 0)
{
Q->rear = Q->front;
Q->front->next = NULL;
return true;
}
else
return false;
}
//入队
int EnterQueue(LinkQueue *Q, QueueElemType x)
{
LinkQueueNode *NewNode;
Newnode = (LinkQueueNode *)malloc(sizeof(LinkQueueNode));
if (NewNode != NULL)
{
NewNode->data = x;
NewNode->next = NULL;
Q->rear->next = NewNode;
Q->rear = NewNode;
return true;
}
else
retrun false;
}
//出队
int DeleteQueue(LinkQueueNode *Q, QueueElemType *x)
{
LinkQueueNode *p;//用于free的
if(Q->front == Q->rear)
return false;
p = Q->front->next;
Q->front->next = p->next;
if(Q->rear == p)//如果队中只有一个p,pfree之后,rear就指向乱七八糟了,所以要改一下rear。
Q->rear = Q->front;
*x = p->data;
free(p);
return true;
}
- 循环队列
#define MAXSIZE 50
typedef struct
{
QueueElementType element[MAXSIZE];
int front;
int rear;
}SeqQueue;
//初始化
void InitQueue(SeqQueue *Q)
{
Q->front = Q->rear = 0;
}
//入队
int EnterQueue(SeqQueue *Q, QueueElementType x)
{
if((Q->rear + 1)%MAXSIZE == Q->front)//尾指针追上头指针
return false;
Q->element[Q->rear] = x;
Q->rear = (Q->rear+1)%MAXSIZE;
return true;
}
//出队
int DeleteQueue(SeqQueue *Q, QueueElementType *x)
{
if(Q->front == Q->rear)
return false;
*x = Q->element[Q->front];
Q->front = (Q->front+1)%MAXSIZE;
return true;
}
3.2.3队列的应用举例
1.打印杨辉三角
#include 2.键盘输入缓冲区算法
seqqueue.h
#define TRUE 1
#define FALSE 0
#define QueueElementType char
#define MAXSIZE 50 /*队列的最大长度*/
typedef struct
{
QueueElementType element[MAXSIZE]; /* 队列的元素空间*/
int front; /*头指针指示器*/
int rear; /*尾指针指示器*/
}SeqQueue;
/*初始化操作*/
void InitQueue(SeqQueue *Q)
{
/* 将*Q初始化为一个空的循环队列 */
Q->front=Q->rear=0;
}
/*入队操作*/
int EnterQueue(SeqQueue *Q, QueueElementType x)
{
/*将元素x入队*/
if((Q->rear+1)%MAXSIZE==Q->front) /*队列已经满了*/
return(FALSE);
Q->element[Q->rear]=x;
Q->rear=(Q->rear+1)%MAXSIZE; /* 重新设置队尾指针 */
return(TRUE); /*操作成功*/
}
/*出队操作*/
int DeleteQueue(SeqQueue *Q, QueueElementType *x)
{
/*删除队列的队头元素,用x返回其值*/
if(Q->front==Q->rear) /*队列为空*/
return(FALSE);
*x=Q->element[Q->front];
Q->front=(Q->front+1)%MAXSIZE; /*重新设置队头指针*/
return(TRUE); /*操作成功*/
}
int GetHead(SeqQueue *Q, QueueElementType *x)
{
/*提取队列的队头元素,用x返回其值*/
if(Q->front==Q->rear) /*队列为空*/
return(FALSE);
*x=Q->element[Q->front];
return(TRUE); /*操作成功*/
}
int IsEmpty(SeqQueue *Q)
{
/*提取队列的队头元素,用x返回其值*/
if(Q->front==Q->rear) /*队列为空*/
return(TRUE);
else
return(FALSE); /*操作成功*/
}
main.c
#include "stdio.h"
#include "conio.h"
#include "seqqueue.h"
main()
{
char ch1,ch2;
SeqQueue Q;
int f;
InitQueue (&Q);/*初始化队列*/
while(TRUE)
{
while(TRUE)
{
printf("A"); /*进程1*/
if(kbhit()) /*前键盘敲击*/
{
ch1=getch(); /*读取键入字符*/
if(ch1==';'||ch1=='.') /*第一个进程中断*/
break;
f= EnterQueue(&Q,ch1); /*入队*/
if(f==FALSE)
{
printf("full"); /*满队*/
break;
}
}
}
while (!IsEmpty(&Q)) /*第二个进程*/
{
DeleteQueue(&Q,&ch2);
putchar(ch2); /*显示输入缓冲区内容*/
}
getch();
if(ch1=='.') break; /*结束整个程序*/
}
}
3.3总结与提高
-
基本概念:
① 栈和队列是特殊的线性表,是操作受限制的线性表
② 操作的位置限制在表的端点
• 栈:限定元素的操作只在表的一端
• 队列:限定元素的操作在表的两段进行 -
顺序和链式存储方式:
① 栈:
• 顺序栈:受到事先开辟的栈区容量的限制;
• 链栈:栈顶指针指向栈顶位置
② 队列:
• 循环队列:为了区分队列空和满的方法(损失一个空间的方法);受到事先开辟的栈区容量的限制;
• 链队列:除了头指针,还有一个尾指针,并且封装在一个结构体里 -
栈与队列的应用:
① 栈:
• 保存暂时无法解决的问题,而将注意力转向最新出现的问题,当最新问题得到解决后,再次回到次新问题上
• 利用最新问题的解,求得次新问题的解(递归)
② 队列:控制解决问题的顺序,凡是对元素的保存次序与使用顺序相同的,都可使用队列