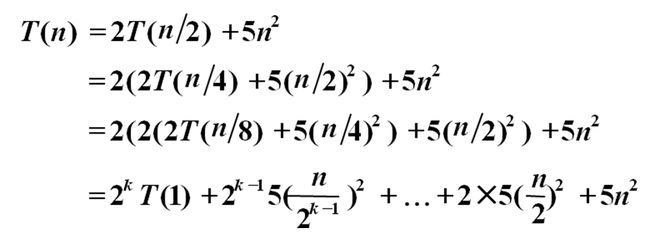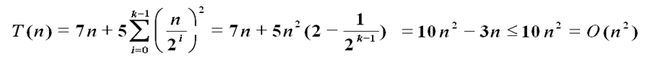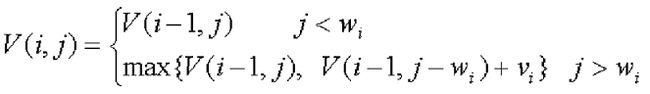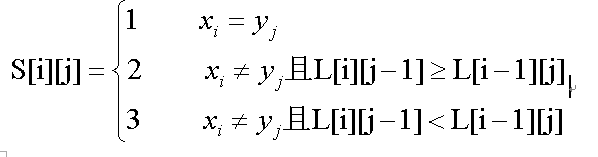大学算法分析与设计复习总结
大学算法分析与设计复习总结
为了拿大学的那悲剧的学分,好好弄懂以下所有知识点吧。把老师的复习的提纲,特意汇总了所有考点,方便童鞋们复习。不喜勿喷!!!
这本书是《算法设计与分析》 王红梅 编著
一共有以下12章,我们学了1、3、4、5、6、7、8、9
分别是“绪论、蛮力法、分治法、减治法、动态规划法、贪心法、回溯法、分治限界法
第1章 绪论
考点:
1、 算法的5个重要特性。(P3)
答:输入、输出、有穷性、确定性、可行性
2、 描述算法的四种方法分别是什么,有什么优缺点。(P4)
答:
1.自然语言 优点:容易理解;缺点:容易出现二义性,并且算法都很冗长。
2.流程图 优点:直观易懂;缺点:严密性不如程序语言,灵活性不如自然语言。
3.程序设计语言 优点:用程序语言描述的算法能由计算机直接执行;缺点:抽象性差,是算法设计者拘泥于描述算法的具体细节,忽略了“好”算法和正确逻辑的重要性,此外,还要求算法设计者掌握程序设计语言及其编程技巧。
伪代码 优点:表达能力强,抽象性强,容易理解
3、 了解非递归算法的时间复杂性分析。(P13)
要点:对非递归算法时间复杂性的分析,关键是建立一个代表算法运行时间的求和表达式,然后用渐进符号表示这个求和表达式。
非递归算法分析的一般步骤是:
(1)决定用哪个(或哪些)参数作为算法问题规模的度量。
(2)找出算法的基本语句。
(3)检查基本语句的执行次数是否只依赖问题规模。
(4)建立基本语句执行次数的求和表达式。
(5)用渐进符号表示这个求和表达式。
[例1.4]:求数组最小值算法
int ArrayMin(int a[ ], int n)
{
min=a[0];
for (i=1; i
if (a[i]
return min;
}
问题规模:n
基本语句: a[i]
T(n)= n-1=O(n)
4、 掌握扩展递归技术和通用分治递推式的使用。(P15)
扩展递归技术:
通用分支递归式:
5、 习题1-4,习题1-7
设计算法求数组中相差最小的两个元素(称为最接近数)的差。要求给出伪代码描述,并用一组例子进行跟踪验证,写出验证过程。
(1)伪代码
1.令最小距离min等于数组头两个元素R[0]和R[1]的差的绝对值;
2.从i=0循环至i
2.1分别求其与j=i+1至j
2.2如果此值小于最小距离,则令新的最小距离为此值;
3.输出最小距离。
(2)用实例进行跟踪验证
R[6]={10,5,11,16,30,14},n=6;
Min=|10-5|=5;
i=0,j=1, |R[i]-R[j]|=|10-5|=5;
j=2,|R[i]-R[j]|=|10-11|=1
j=3, |R[i]-R[j]|=|10-16|=6;
j=4, |R[i]-R[j]|=|10-30|=20;
j=5, |R[i]-R[j]|=|10-14|=4;
i=1,j=2, |R[i]-R[j]|=|5-11|=6;
j=3, |R[i]-R[j]|=|5-16|=11;
j=4, |R[i]-R[j]|=|5-30|=15;
j=5, |R[i]-R[j]|=|5-14|=9;
i=2,j=3, |R[i]-R[j]|=|11-16|=5;
j=4, |R[i]-R[j]|=|11-30|=19;
j=5, |R[i]-R[j]|=|11-14|=3;
i=3,j=4, |R[i]-R[j]|=|16-30|=14;
j=5, |R[i]-R[j]|=|16-14|=2;
i=4,j=5, |R[i]-R[j]|=|30-14|=16;
最后输出min=1
7、使用扩展递归技术求解下列递推关系式
(1)
(2)

第3章 蛮力法
1、 掌握蛮力法的设计思想:
蛮力法依赖的基本技术——扫描技术,即采用一定的策略将待求解问题的所有元素依次处理一次,从而找出问题的解;
关键——依次处理所有元素。
2、 蛮力法的代表算法及其时间复杂度:
顺序查找,O(n)
串匹配(BF O(n*m) ,KMPO(n+m) , BMO(n*m))
选择排序,O(n2)
冒泡排序,O(n2)
生成排列对象(排列问题),O(n!)
生成子集(组合问题),O(2n)
0/1背包 属于组合问题。
任务分配,哈密顿回路,TSP问题 属于排列问题。
最近对问题 O(n2),凸包问题 O(n3)
3、 掌握BF和KMP算法的原理,能够画出比较过程。P71习题3的4。要求给出一串字符串,能够求出对应的next数组,并能使用KMP算法进行比较匹配。
4、 掌握选择排序和冒泡排序算法描述和时间复杂性,要求能够写出伪代码。(P56-58)
选择排序
算法描述:选择排序开始的时候,扫描整个序列,找到整个序列的最小记录和序列中的第一记录交换,从而将最小记录放到它在有序区的最终位置上,然后再从第二个记录开始扫描序列,找到n-1个序列中的最小记录,再和第二个记录交换位置。一般地,第i趟排序从第i个记录开始扫描序列,在n-i+1个记录中找到关键码最小的记录,并和第i个记录交换作为有序序列的第i个记录。
时间复杂性:O(n2)
伪代码:
冒泡排序
算法描述:冒泡排序开始的时候扫描整个序列,在扫描过程中两两比较相邻记录,如果反序则交换,最终,最大记录就能被“沉到”了序列的最后一个位置,第二趟扫描将第二大记录“沉到”了倒数第二个位置,重复上述操作,直到n-1趟扫描后,整个序列就排好序了。
冒泡排序,O(n2)
5、 算法设计题:习题3-3,3-6,3-8,3-11,3-13
3-3 对于KMP算法中求next数组问题,设计一个蛮力算法,并分析其时间性能。
voidGetNext(char T[ ], int next[ ])
{
next[1]=0;
next[2]=1;
j=T[0],k=0;
for(;j>2;j--){
for(n=j-2;n>=1;n--){//n为要比较的前缀的最后一个字符的下标
m=j-n;//m为要比较的后缀的第一个字符的下标
for(i=1;i<=n;i++)
{
if(T[i]!=T[m+i-1])break;
}
if(i==n+1){next[j]=n+1;break;}
}
if(n==0)next[j]=1;
}
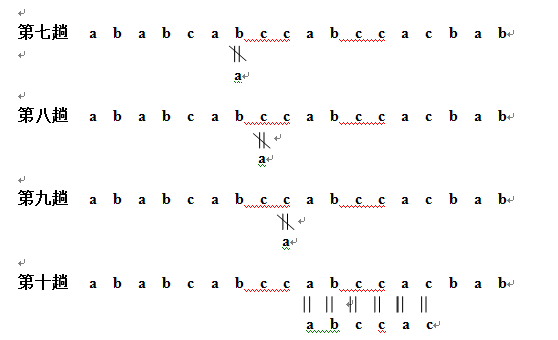
}3-4 假设在文本“ababcabccabccacbab”中查找模式 “abccac”,求分别采用BF算法和KMP算法进行串匹配过程中的字符比较次数。

由此可知,用BF算法一共要进行3+1+4+1+1+6+1+1+1+6=25次比较方能匹配出
KMP算法:next[]={,0,1,1,1,1,2};
由此可知,用KMP算法一共要进行3+4+6+5=18次比较方能匹配出
参考代码如下:
排列最终存储在长度为n的阶乘,元素类型为指针的数组中,数组指向一个排列,具体的排列数据存储在数组中。
int fabs(int n)
{
int r=1;
for(inti=n;i>1;i--)
r=r*i;
return r;
}
//排列存储在数组中
void getArrangement(int**&s,int n)
{
int * p,*q;
int * *s1;
int i,j,k,l,m,o;
s=new int *[1];
s[0]=newint[1];
s[0][0]=1;
for(i=2;i<=n;i++)
{
j=0;
o=0;
m=fabs(i-1);
s1=newint *[fabs(i)];
while(o=0;k--)
{
s1[j]=newint[i];
for(l=0;l
3-8对于一个平面上n个点的集合S,设计蛮力算法求集合S的凸包的一个极点。
点集合中最左边或者最右边的点一定是凸包的一个极点,则求凸包的极点的问题转化为求点的x坐标最大或最小的点
int getPole(int x[],int y[],int n)
{
int r=0;
for(inti=0;ix[r])r=i;
}
return r;
} 3-11 设计算法生成在n个元素中包含k个元素的所有组合对象。
两种思路:
1、 生成所有的组合,在组合中找元素个数为k个的组合。
伪代码:
1.初始化一个长度为n的比特串s=00…0并将对应的子集输出;
2.for(i=1; i<2n; i++) //注意不能书写成i<=2n
2.1 s++;
2.2 判断s中1的个数,若为k,则将s对应的子集输出;
2、 使用k层嵌套循环生成元素个数为k个的组合。
设k=3;n个元素存储在数组a[]中;
伪代码:
for (i=1; i
for(j=i+1; i
for(k=j+1; i
输出a[i]a[j]a[k]构成的组合。
3-13美国有个连锁店叫7-11这个连锁店以前是每天7点开门,晚上11点关门
不过现在是全天24小时营业。有一天,有个人来到这个连锁店,买了4件商品
营业员拿起计算器敲了一下,说:总共是$7.11顾客开玩笑说:所以你们商店就叫7-11?营业员没有理她,说:当然不是,我是把它们的价格相乘之后得到的。
顾客说:相乘?你应该把他相加才对。营业员说,我弄错了。接着又算了一遍,结果让两个人吃惊的是:计算结果也是$7.11请问,这4件商品的价格是多少?
参考代码:
#include
#include
int main()
{
long i,j,k,m;
for (i=1; i <=711/4 ; i++)
{
for (j=i; j <=711/3 ; j++)
{
for (k=j; k <=711/2 ; k++)
{
m=711-i-j-k;
if (i*j*k*m==711*1000000)
{
cout< 输出结果为:价格分别是1.2 1.251.5 3.16
第4章 分治法
了解分治法的设计思想
设计思想:将要求解的原问题划分成k个较小规模的子问题,对这k个子问题分别求解。如果子问题的规模仍然不够小,则再将每个子问题划分为k个规模更小的子问题,如此分解下去,直到问题规模足够小,很容易求出其解为止,再将子问题的解合并为一个更大规模的问题的解,自底向上逐步求出原问题的解。
步骤:(1)划分(2)求解子问题(3)合并
分治法的代表算法及时间复杂度:
归并排序,快速排序,最大子段和,最近对问题,凸包问题,这五种问题的分治算法的时间复杂度为O(nlog2n)
棋盘覆盖,循环赛日程安排为O(4k)
掌握归并排序和快速排序算法的算法伪代码。(P78-83)
归并排序:
算法中数组r中存储原始数据,r1在中间过程中存储排序后的数据,s指需排序数组的起始下标,t指需排序数组的结束下标。最终排序后的数据依然存储在r数组中。
快速排序:
掌握最大子段和问题的算法伪代码。(P83-85)
对于待排序列(5, 3, 1, 9, 8, 2, 4, 7),画出快速排序的递归运行轨迹。
按升序排列
初始序列:5,3,1,9,8,2,4,7
第一次划分:4,3,1,2,5,8,9,7
第二次划分:2,3,1,4,5,8,9,7
第三次划分:1,2,3,4,5,8,9,7
第四次划分:1,2,3,4,5,7,8,9
排序完成,红色字体为每次划分的轴值
在有序序列9(r1,r2,```, rn)中,存在序号i ( 1<=i<=n),使得ri = i, 请设计一个分治算法找到这个元素,要求算法在最坏情况下的时间性能为O(log2n).
参考代码:
#include
int findr(ints[],int begin,int end)
{
if(begin==end){
if(s[begin]==begin) return begin;
else return 0;
}else
{
int m=(begin+end)/2;
if(s[m]>m) return findr(s,begin,m-1);
else if (s[m]==m)return m;
else return findr(s,m+1,end);
}
}
void main()
{
int s[]={0,1,1,2,4,6,8};
cout< 第5章 减治法
了解减治法的设计思想
设计思想:原问题的解只存在于其中一个较小规模的子问题中,所以,只需求解其中一个较小规模的子问题就可以得到原问题的解。
掌握使用减治法的代表问题及时间复杂度:
折半查找,二叉树查找,堆排序,选择问题,淘汰赛冠军问题,假币问题;
以上问题的时间复杂度,如果减治是每次减小为原来规模的1/2,则时间复杂度一般为O(log2n)
掌握折半查找的算法伪代码描述及具体例子的查找过程,会根据折半查找的过程创建判定树。(P98-100)
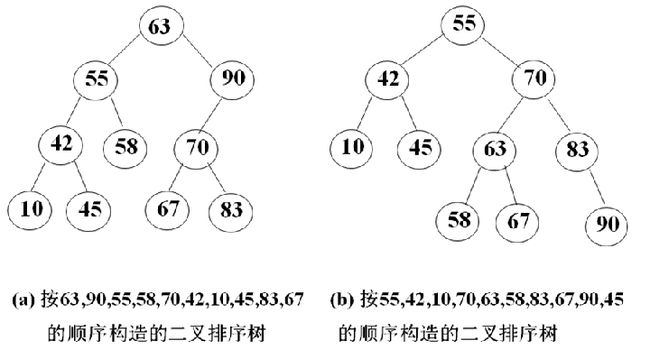
会根据已知数据序列创建一个二叉查找树。(P100)
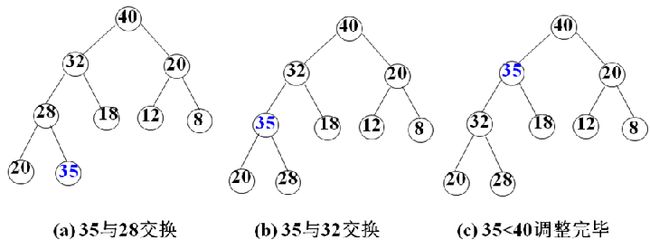
掌握堆排序算法中的两种调整堆和新建堆的方法:筛选法和插入法(P101-105)
堆调整问题:将一个无序序列调整为堆
(1)筛选法调整堆
关键问题:完全二叉树中,根结点的左右子树均是堆,如何调整根结点,使整个完全二叉树成为一个堆? 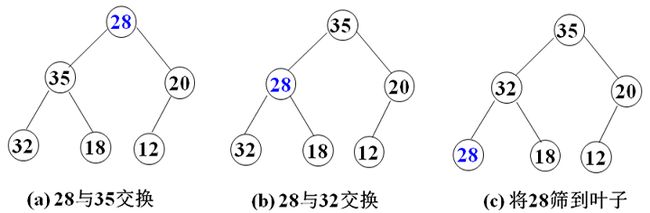
(2)插入法调整堆
关键问题是:在堆中插入一个结点,如何调整被插入结点,使整个完全二叉树仍然是一个堆?
掌握选择问题的算法的伪代码(P105-106)
习题5-1,算法设计题
习题5-4,给出任意一组数据,能分别用筛选法和插入法写出创建堆的过程,并用两种方法进行堆排序。
对(47,5,26,28,10)进行筛选堆排序,使用大根堆,形成升序 ,列出每次筛选后的序列
形成大根堆的过程(先把数组直接表示成完全二叉树):
47,5,26,28,10(叶子结点,不用筛选)
47,5,26,28,10 (叶子结点,不用筛选)
47,5,26,28,10 (叶子结点,不用筛选)
47,5,26,28,10
47,28,26,5,10 (5与两个孩子中的大者比较,5小,交换位置)
47,28,26,5,10 (47与两个孩子中的大者比较,47大,不用交换位置)
47,28, 26, 5 ,10 (大根堆)
10,28, 26, 5 , 47 (取出堆顶元素后的序列)
10,28, 26, 5 , 47 (筛选)
28, 10 , 26, 5 , 47
28, 10 , 26, 5 , 47 (大根堆)
5, 10 , 26, 28, 47 (取出堆顶元素后的序列)
5, 10 , 26, 28, 47 (筛选)
26, 10 , 5, 28, 47
26, 10 , 5, 28, 47 (大根堆)
5, 10 , 26, 28, 47 (取出堆顶元素后的序列)
5, 10 , 26, 28, 47 (筛选)
10, 5 , 26, 28, 47
10, 5 , 26, 28, 47 (大根堆)
5, 10 , 26, 28, 47 (取出堆顶元素后只剩一个值,结束算法)
对(47,5,26,28,10)进行插入法生成大根堆
47
47 5
47 5 26
47 28 26 5
47 28 26 5 10
第6章 动态规划法
了解动态规划法的设计思想
设计思想:将待求解问题分解成若干个相互重叠的子问题,每个子问题对应决策过程的一个阶段,将子问题的解求解一次并填入表中,当需要再次求解此子问题时,可以通过查表获得该子问题的解而不用再次求解。
步骤:
将原始问题分解为相互重叠的子问题,确定动态规划函数;
求解子问题,填表;
根据表,自底向上计算出原问题的解。
掌握可以用动态规划法解决的问题及时间复杂度:
TSP,多段图的最短路径问题,0/1背包,最长公共子序列问题,最优二叉查找树,近似串匹配问题;
多段图的最短路径问题: O(n+m)
0/1背包问题: O(n×C)
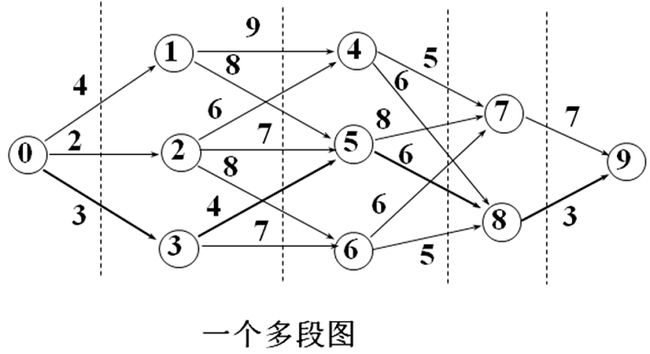
掌握多段图的最短路径问题的动态规划算法及具体实现(P121-123),习题6-2
动态规划函数为:
cost[i]中存储顶点i到终点的最短路径长度
cost[i]=min{C[i][j]+cost[j]} (i≤j≤n且顶点j是顶点i的邻接点)
path[i]=使C[i][j]+cost[j]最小的j
先构造cost数组和path数组
掌握0/1背包问题的动态规划算法及具体实现(P123-126),习题6-3
例题:用动态规划法求如下0/1背包问题的最优解:有5个物品,其重量分别为(3,2,1,4,5),物品的价值分别为(25,20,15,40, 50),背包容量为6。写出求解过程。
0/1背包问题的动态规划函数为:
V(i,j)表示把前i个物品放入容量为j的背包中的最大价值和。
填表过程:
放入背包中的物品的求解过程:则65表示把5个物品放入容量为6的背包中的最大价值和。
i=5,j=6; v[5][6]>v[4][6],x[5]=1, j=6-w[5]=1
i=4,j=1;v[4][1]=v[3][1], x[4]=0
i=3,j=1;v[3][1]>v[2][1], x[3]=1, j=1-w[3]=0
i=2,j=0;v[2][1]=v[1][0], x[2]=0
i=1,j=0;v[1][0]=v[0][0], x[1]=0
结果是把第3个和第5个放入了背包
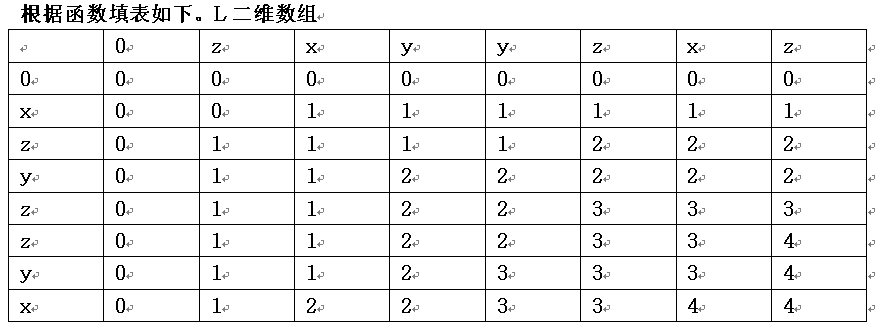
掌握最长公共子序列问题的动态规划法算法及具体实现(P126-128),习题6-4
求X=“xzyzzyx”和Y=“zxyyzxz”序列的最长公共子序列的动态规划函数为:
L[i][j]表示X中前i个元素和Y中前j个元素构成的序列的最长公共子序列的长度。
为了确定具体的最长公共子序列,需要同时计算S[i][j]的值,S[i][j]表示在计算L[i][j]的过程中的搜索状态。
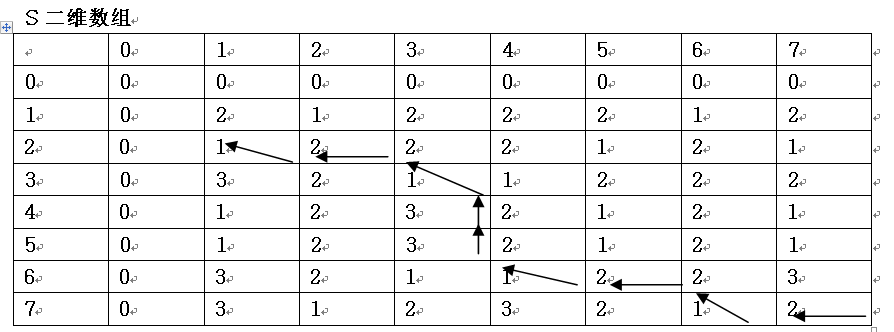
子序列为斜箭头所标示的行或列:X[2],X[3],X[6] ,X[7]或Y[1], Y[3], Y[4] , Y[6]最长公共子序列的长度为4
即为:zyyx
第7章 贪心法
了解贪心法的设计思想
贪心法在解决问题的策略上目光短浅,只根据当前已有的信息就做出局部最优选择,而且一旦做出了选择,不管将来有什么结果,这个选择都不会改变。
贪心法的关键在于决定贪心策略。
掌握可以用贪心法解决的问题:
TSP问题中的两种解决方法:最近领点策略,最短链接策略
最小生成树问题的两种算法:最近顶点策略(Prim算法),最短边策略(Kruskal算法)
背包问题,活动安排问题,多机调度问题,哈夫曼编码。
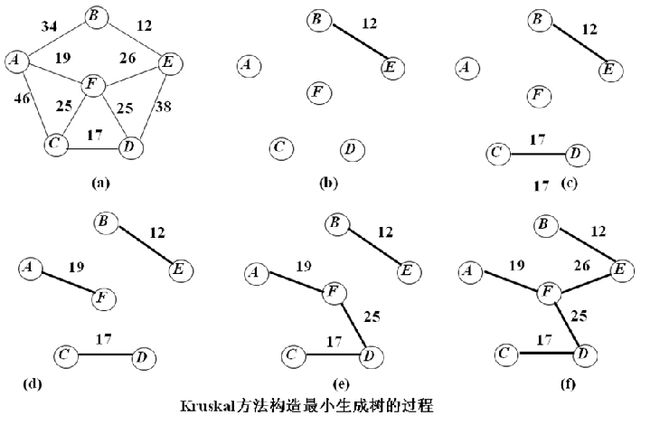
掌握最小生成树的两种贪心算法:prim算法和kruskal算法(P145-148),给出具体的例子,能够用两种方法画出树的生成过程。
掌握背包问题的贪心算法(P148-151),给出一个具体的例子,能够写出解决问题的过程。习题7-2
问题:求如下背包问题的最优解:有7个物品,价值P=(10,5,15,7,6,18,3),重量w=(2,3,5,7,1,4,1),背包容量W=15.
解决方法:
先对物品的单位重量价值按照降序排列
| 物品重量 |
物品价值 |
物品价值/物品重量 |
| 1 |
6 |
6 |
| 2 |
10 |
5 |
| 4 |
18 |
4.5 |
| 5 |
15 |
3 |
| 1 |
3 |
3 |
| 3 |
5 |
1.67 |
| 7 |
7 |
1 |
依次把物品放入容量为15的背包,直到背包被装满
1+2+4+5+1=13,前5个物品装入背包,还剩下容量为2,第6个物品只能装入2/3
所以总价值为:6+10+18+15+3+5*2/3=55.3333
给出字符集和对应的频率,能够画出对应的哈夫曼树,并对给定的字符串进行哈夫曼编码。(P155-157)
第8章 回溯法
了解回溯法的设计思想
设计思想:从解空间树根结点出发,按照深度优先策略遍历解空间树,在搜索至树中任一结点时,先判断该结点对应的部分解是否满足约束条件,或者是否超出目标函数的界,也就是判断该结点是否包含问题的(最优)解,如果肯定不包含,则跳过对以该结点为根的子树的搜索,即所谓剪枝(Pruning);否则,进入以该结点为根的子树,继续按照深度优先策略搜索。直到搜索到叶子结点,则得到问题的一个可能解。
步骤:
确定解向量和分量的取值范围,构造解空间树;
确定剪枝函数;
对解空间树按深度优先搜索,搜索过程中剪枝;
从所有的可能解中确定最优解。
了解可以用回溯法解决的问题:
属于组合问题和排列问题中求最优解的问题都可以用回溯法解决,例如:图着色问题,哈密顿回路问题,八皇后问题(4皇后问题),批处理作业调度问题。
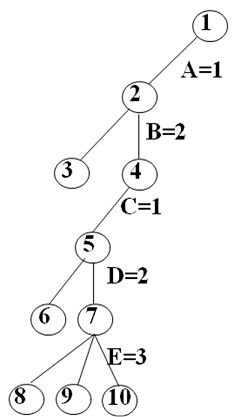
掌握m颜色图着色判定问题的回溯法算法,并能画出解空间树的搜索过程(P168-170),习题8-4
对图8.14使用回溯法求解图问题,画出生成的搜索空间。
解:图着色问题求解的是满足图着色要求的最小颜色数。对图8.14应该从1、2、3、4……种颜色依次尝试用回溯法判定是否满足M着色的要求。
经搜索,1种和2种颜色均不能满足图着色的要求,3种颜色可以满足图着色要求,搜索过程如下,所以图8.14的着色的最少颜色数应该为3
搜索空间为:
掌握n皇后问题的回溯法算法,并能画出解空间树的搜索过程(P173-174),
自己看书
掌握0/1背包问题的回溯算法,并能画出解空间树的搜索过程(P163-164),习题8-5
自己看书
习题8-6,算法设计题。
给定一个正整数集合X={x1,x2,…, xn}和一个正整数y,设计回溯算法,求集合X的一个子集Y,使得Y中元素之和等于y。
解:
用回溯法求解问题分析:
该问题为求子集问题。
解分量的和小于y为剪枝函数。
当搜索到结点,并且解分量的和等于y时,找到问题的解。
1.X={x1,x2,x3……xn },sum=0,Y={ }为解向量,初始化为全0;
2.flag=false;
3.k=1;
4.while (k>=1)
4.1 当(Sk取1、0)循环执行下列操作
4.1.1yk=Sk中的下一个元素;
4.1.2将yk加入Y;
4.1.3sum=+(yk?xk:0);
4.1.4if (sum==y) flag=true; 转步骤5;
4.1.4else if (sum
4.2 重置Sk,使得下一个元素排在第1位;
4.3 k=k-1; //回溯
5.if flag 输出解Y;
else 输出“无解”;
参考代码:
#include
const int N=5;
int f(int x[],int y[],int n)
{
//初始化y,y为所求的集合
for(inti=0;i=0)
{
y[k]=y[k]-1;
if((y[k]==1||y[k]==0)&&k 第9章 分治限界法
了解分支限界法的设计思想
设计思想:
1)首先确定一个合理的限界函数,并根据限界函数确定目标函数的界[down, up] ,并确定限界函数;
2)然后按照广度优先策略遍历问题的解空间树,在分支结点上,依次搜索该结点的所有孩子结点,分别估算这些孩子结点的限界函数的可能取值;
3)如果某孩子结点的限界函数可能取得的值超出目标函数的界,则将其丢弃;否则,将其加入待处理结点表(以下简称表PT)中;
4)依次从表PT中选取使限界函数的值是极值的结点成为当前扩展结点;
5)重复上述过程,直到找到搜索到叶子结点,如果叶子结点的限界函数的值是极值,则就是问题的最优解,否则,找到其他极值结点重复扩展搜索。
步骤:
确定解空间树
确定限界函数
按广度优先搜索解空间树,计算限界函数的值,填入PT表
从PT表中寻找极值,继续扩展结点,直到找到限界函数值为极值的叶子结点。
了解可以使用分支限界法解决的问题:
TSP问题,多段图的最短路径问题,任务分配问题,批处理作业调度问题,0/1背包问题。
掌握任务分配问题的分支限界法(P195-197),习题9-5
掌握0/1背包问题的分支限界法(P184-185),习题9-6
掌握批处理作业问题的分支限界法(P198-200),习题9-7