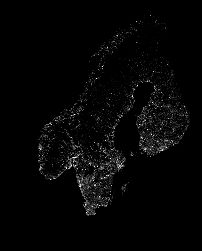
SIR模型与病毒地理传播可视化
文章目录
- 开篇一张图
- 传染病 SIR 模型
- 代码
- SIR
- 准备一张人口密度图
- 欧拉方法求解初值问题的数值解
- 自定义 colormap
- 画 GIF 动图
- 参考博客
开篇一张图
传染病 SIR 模型
- S 表示健康人数
- I 表示感染人数
- R 表示康复人数
u ( t ) = ( S I R ) u(t) = \begin{pmatrix} S \\ I \\ R \end{pmatrix} u(t)=⎝⎛SIR⎠⎞
演化的动力学模型为一阶常微分方程组:
f ( u ) = u ′ ( t ) = ( S ′ I ′ R ′ ) = ( − β I S β I S − γ I γ I ) u n + 1 = f ( u ) Δ t + u n f(u) = u'(t) = \begin{pmatrix} S' \\ I' \\ R' \end{pmatrix} = \begin{pmatrix} -\beta I S \\ \beta I S - \gamma I \\ \gamma I \end{pmatrix} \\ u_{n+1} = f(u)\Delta t + u_n f(u)=u′(t)=⎝⎛S′I′R′⎠⎞=⎝⎛−βISβIS−γIγI⎠⎞un+1=f(u)Δt+un
模型里有两个参数: β , γ \beta, \gamma β,γ 分别表示传染速率与康复速率。
以上模型描述的是单个群体内患病者数量的变化。
如果要考虑地理空间上的传播,还要进一步修改模型。不妨假设地理空间是网格划分的,传染病可以通过相邻格点进行传播。
显然这个模型是不靠谱的,但用来可视化还是可以一试:
f ( u ) = u ′ ( t ) = ( S ′ I ′ R ′ ) = ( − β [ S i , j ( I i , j + I i − 1 , j + I i + 1 , j + I i , j − 1 + I i , j + 1 ) ] β [ S i , j ( I i , j + I i − 1 , j + I i + 1 , j + I i , j − 1 + I i , j + 1 ) ] − γ I i , j γ I i , j ) f(u) = u'(t) = \begin{pmatrix} S' \\ I' \\ R' \end{pmatrix} = \begin{pmatrix} -\beta \left[S_{i,j}(I_{i,j} + I_{i-1,j} + I_{i+1,j} + I_{i,j-1} + I_{i,j+1})\right] \\ \beta \left[S_{i,j}(I_{i,j} + I_{i-1,j} + I_{i+1,j} + I_{i,j-1} + I_{i,j+1})\right] - \gamma I_{i,j} \\ \gamma I_{i,j} \end{pmatrix} f(u)=u′(t)=⎝⎛S′I′R′⎠⎞=⎝⎛−β[Si,j(Ii,j+Ii−1,j+Ii+1,j+Ii,j−1+Ii,j+1)]β[Si,j(Ii,j+Ii−1,j+Ii+1,j+Ii,j−1+Ii,j+1)]−γIi,jγIi,j⎠⎞
代码
import numpy as np
import math
import matplotlib.pyplot as plt
%matplotlib inline
from matplotlib import rcParams
import matplotlib.image as mpimg
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 16
rcParams['figure.figsize'] = 12, 8
from PIL import Image
SIR
beta = 0.010
gamma = 1
def f(u):
S = u[0]
I = u[1]
R = u[2]
I_neighbors = I[1:-1, 1:-1] + I[0:-2, 1:-1] + I[2:, 1:-1] + I[1:-1, 0:-2] + I[1:-1, 2:]
I_new = beta*S[1:-1, 1:-1]*I_neighbors
R_new = gamma*I[1:-1, 1:-1]
new = np.array([-I_new,
I_new - R_new,
R_new
])
padding = np.zeros_like(u)
padding[:,1:-1,1:-1] = new
padding[0][padding[0] < 0] = 0
padding[0][padding[0] > 255] = 255
padding[1][padding[1] < 0] = 0
padding[1][padding[1] > 255] = 255
padding[2][padding[2] < 0] = 0
padding[2][padding[2] > 255] = 255
return padding
准备一张人口密度图
from PIL import Image
img = Image.open('popdensity.png')
img = img.resize((img.size[0]//2,img.size[1]//2))
img = 255 - np.asarray(img)
plt.imshow(img)
欧拉方法求解初值问题的数值解
初值条件为:
- S 健康人数等于人口密度图的数值
- I 感染数初始为 0,将疾病爆发的地点设为 1
- R 康复数初始为 0
S_0 = img[:,:,1]
I_0 = np.zeros_like(S_0)
I_0[309,170] = 1 # patient zero
R_0 = np.zeros_like(S_0)
T = 600 # final time
dt = 1 # time increment
N = int(T/dt) + 1 # number of time-steps
t = np.linspace(0.0, T, N) # time discretization
# initialize the array containing the solution for each time-step
u = np.empty((N, 3, S_0.shape[0], S_0.shape[1]))
u[0][0] = S_0
u[0][1] = I_0
u[0][2] = R_0
def euler_step(u, f, dt):
return u + dt * f(u)
for n in range(N-1):
u[n+1] = euler_step(u[n], f, dt)
自定义 colormap
如下代码修改透明度,为了使两张图片画在一起
import matplotlib.cm as cm
theCM = cm.get_cmap("Reds")
theCM._init()
alphas = np.abs(np.linspace(0, 1, theCM.N))
theCM._lut[:-3,-1] = alphas
画 GIF 动图
import matplotlib.animation as animation
n_frames = 30
def draw(i):
plt.imshow(img, vmin=0, vmax=255, interpolation="nearest")
plt.imshow(u[i][1], vmin=0, cmap=theCM, interpolation="nearest")
plt.xticks([])
plt.yticks([])
height, width, depth = img.shape
dpi = 100
fig = plt.figure(figsize=(width // dpi, height // dpi))
fig.clf()
ax = fig.subplots()
fps = 3
ani = animation.FuncAnimation(fig, draw, frames=range(0, N-1, N//n_frames), interval=1000/fps, repeat=True)
ani.save('change.gif', writer='pillow', fps=fps)
# plt.show()
结果如开篇所示!
参考博客
模型和画图代码都经过修改,但还是要吃水不忘挖井人:https://github.com/maxberggren/blog-notebooks/blob/master/SweEbola.ipynb