PyMC3 - GLM之鲁棒线性回归

数据产生

上一篇文章中使用的是仿真数据，然而在真实数据中往往存在许多异常值，本文向仿真数据中添加一些异常值来探讨如何增加线性回归的鲁棒性。

%matplotlib inline

import pymc3 as pm
import matplotlib.pyplot as plt
import numpy as np

像上一篇文章一样构造防止数据，但是添加一些异常值。

size = 100
true_intercept = 1
true_slope = 2

# y = a + b*x
x = np.linspace(0, 1, size)
true_regression_line = true_intercept + true_slope * x

# add noise
y = true_regression_line + np.random.normal(scale=0.5, size=size)

# 添加异常值
x_out = np.append(x, [.1, .15, .2])
y_out = np.append(y, [8, 6, 9])

data = dict(x=x_out, y=y_out)

画出原始数据的图形可以看到三个偏离的较远的异常点。

fig = plt.figure(figsize=(7, 7));
ax = fig.add_subplot(111, xlabel='x', ylabel='y', title='Generated data and underlying model');
ax.plot(x_out, y_out, 'x', label='sampled data');
ax.plot(x, true_regression_line, label='true regression line', lw=2.0);
plt.legend(loc=0);

传统贝叶斯线性回归模型

如果用之前的方法进行贝叶斯线性回归得到的结果。这里使用 glm() 模块进行，这个模型可以接受Patsy字符串进行线性模型描述，并且在默认情况下会添加正态似然函数。

with pm.Model() as model:
    pm.glm.glm('y ~ x', data)
    trace = pm.sample(2000)

Auto-assigning NUTS sampler...
Initializing NUTS using advi...
Average ELBO = -199.17: 100%|██████████| 200000/200000 [00:23<00:00, 8583.33it/s] 
Finished [100%]: Average ELBO = -199.18
100%|██████████| 2000/2000 [00:05<00:00, 344.31it/s]

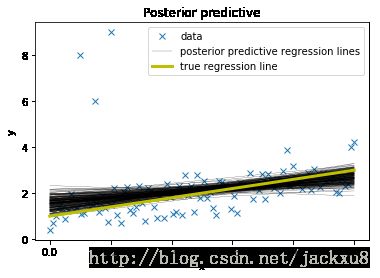
将后验估计的回归直线和真实直线同时绘制来看出参数估计的效果。可以看出，估计的结果有较大的偏斜；并且对于带估计的参数的后验分布有一个很宽的置信区间。这是由于对于正态分布没有一个宽的尾巴导致的，因此异常点的影响较为严重。

在频率学派中有一个鲁棒回归Robust Regession的方法，使用非二次方距离作为距离测量方法。

plt.subplot(111, xlabel='x', ylabel='y', title='Posterior predictive regression lines')
plt.plot(x_out, y_out, 'x', label='data')
pm.glm.plot_posterior_predictive(trace, samples=200, label='posterior predictive regression lines')
plt.plot(x, true_regression_line, label='true regression line', lw=3., c='y')
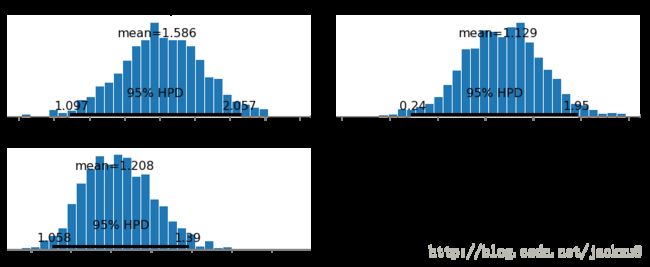
plt.legend(loc=0);

pm.plot_posterior(trace);

鲁棒贝叶斯线性回归模型

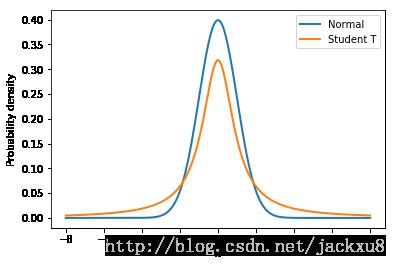
由于问题的关键是正态分布过小的尾巴引起的，那么我们可以假设我们的数据先验分布是一个大尾巴分布-Student T 分布，下图展示了正态分布和StudentT 分布的区别，特别注意其尾部的区别。

normal_dist = pm.Normal.dist(mu=0, sd=1);
t_dist = pm.StudentT.dist(mu=0, lam=1, nu=1);
x_eval = np.linspace(-8, 8, 300);
plt.plot(x_eval, pm.math.exp(normal_dist.logp(x_eval)).eval(), label='Normal', lw=2.)
plt.plot(x_eval, pm.math.exp(t_dist.logp(x_eval)).eval(), label='Student T', lw=2.)
plt.xlabel('x');
plt.ylabel('Probability density');
plt.legend();

在模型定义中，可以使用family变量来指定数据是 StudentT分布的（在 glm.families中有更多的描述）。

??pm.glm.families

with pm.Model() as model_robust:
    family = pm.glm.families.StudentT()
    pm.glm.glm('y ~ x', data, family=family)
    trace_robust = pm.sample(2000)

Auto-assigning NUTS sampler...
Initializing NUTS using advi...
Average ELBO = -148.4: 100%|██████████| 200000/200000 [00:21<00:00, 9428.66it/s] 
Finished [100%]: Average ELBO = -148.41
100%|██████████| 2000/2000 [00:04<00:00, 475.56it/s]

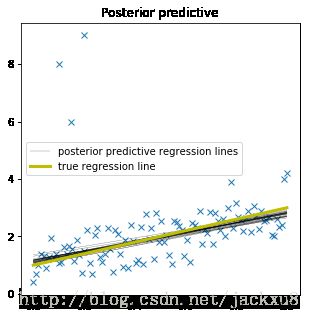
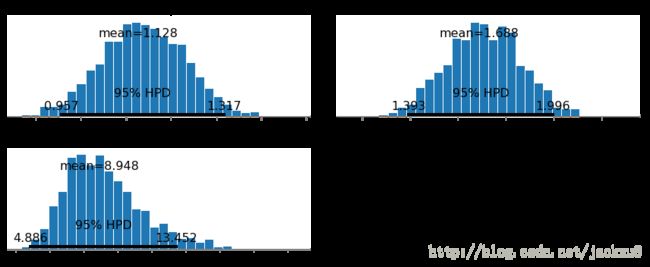
可以看出，拟合的结果更好，说明参数估计的更加准确，可能的范围也更小。

plt.figure(figsize=(5, 5))
plt.plot(x_out, y_out, 'x')
pm.glm.plot_posterior_predictive(trace_robust,label='posterior predictive regression lines')
plt.plot(x, true_regression_line, label='true regression line', lw=3., c='y')
plt.legend();

pm.plot_posterior(trace_robust);