抗碰撞性、生日攻击及安全散列函数结构解析
回顾一下,密码学的上篇是完整性,完整性的保证是由一段定长的散列,俗称tag来确定的。又因为tag是定长的,而需要确保完整性的内容种类却可以认为是无限的。因此总有tag(mi)=tag(mj),mi != mj,因此我们要引入抗碰撞性这个概念。
抗碰撞性:
抗碰撞性(Collision-Resistant):找出任意两个不同的x,x' \in X,使得h(x)=h(x')是困难的(计算不可行);也称强抗碰撞性(Strong Collision-Resistant )。相对的,也有弱抗碰撞性(Weak Collision-Resistant )这个概念。
弱抗碰撞性:当给定某条消息的散列值时,单向散列函数必须确保要找到和该条消息具有相同散列值的另外一条消息是非常困难的。
强抗碰撞性:是指要找到散列值相同的两条不同的消息是非常困难的。
强抗碰撞性:是指要找到散列值相同的两条不同的消息是非常困难的。
而针对碰撞性的攻击,最主要的要数生日攻击了:
生日攻击(Birthday Attack):
生日悖论(Birthday paradox):
生日悖论是指,如果一个房间里有23个或23个以上的人,那么至少有两个人的生日相同的概率要大于50%。这就意味着在一个典型的标准小学班级(30人)中,存在两人生日相同的可能性更高。对于60或者更多的人,这种概率要大于99%。从引起逻辑矛盾的角度来说生日悖论并不是一种悖论,从这个数学事实与一般直觉相抵触的意义上,它才称得上是一个悖论。大多数人会认为,23人中有2人生日相同的概率应该远远小于50%。
证明:
在考虑所有人的生日都是独立均匀随机分布在365内的话,
因为第二个人不能跟第一个人有相同的生日(概率是364/365),第三个人不能跟前两个人生日相同(概率为363/365),依此类推。用阶乘可以写成如下形式:
由此可得,当n=23时,概率趋于50%,而人的出生率并不是均匀随机的,因此23人实际概率应该大于50%。
生日攻击原理:
由此我们可以将它用在碰撞,得到不同Message有着相同tag。
假设:取样次数为N,M:M1-Mn,取值在tag:1-B中,并且假设分布随机均匀相互独立。
取样次数n与B的关系,n=1.2*B^0.5(这是生日悖论中最坏的情况。)
证明:M2不等于M1的概率为(B-1)/B,同理可得M3为(B-2)/B,M4为(B-3)/B...Mn为(B-n+1)/B。
因此,其中有碰撞的概率为:1-(1-1/B)(1-2/B).....(1-(k-1)/B)>= (1-e)^(-n^2/2B)
因为n=1.2*B^0.5,因此(1-e)^(-n^2/2B)=1-e^-0.72=0.53>50%
结论,因此使用生日攻击,我们只需2^(n/2)次寻找,就有50%概率能找到相同tag的两个不同Message。
步骤:
1.随机在2^(n/2)信息空间中寻找一个M
2.求出相应的tag
3.寻找是否有碰撞,没有则返回步骤1
破解时间:
理论上而言,若抗碰撞性一直为2^n,而强抗碰撞性因为生日攻击的原因会降至2^(n/2)时间。
由此可见,SHA-1已经越来越不安全了,数月或者数年后,2^80将不是一个无法逾越的计算时间。另外,因为计算机多为伪随机,因此现在SHA-1理论上所需的抗碰撞时间仅为2^55时间,但好像并没有人去证实过。
安全散列函数结构:
因为所需的安全散列长度越来越长,因此我们可以使用有限定义域上的散列函数(俗称压缩函数)通过迭代方式拓展为具有无限定义域的散列函数。而最为代表性的就Merkle-Damgard结构
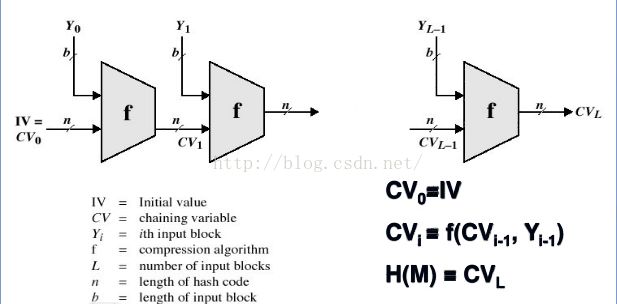
Merkle-Damgard结构:
这个结构的好处是,如果压缩函数是抗碰撞的,那经过此结构处理后的散列函数也是抗碰撞的。
SM3,HMAC就是基于这种结构,因为Merkle-Damgard结构并不能抵抗扩展攻击,因此HMAC引入了Key。