K-means、K-means ++、K-modes和K-prototype聚类算法简述 附Python代码

K-means

K-means属于聚类算法中最简单的一种，也是一种无监督学习的算法。

步骤：

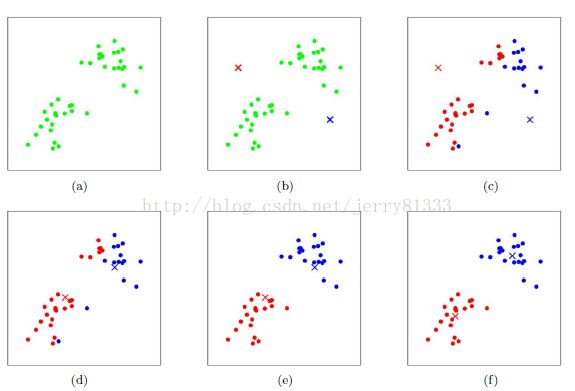
按上图所示，具体步骤如下：

1. 设定初始簇的个数，上图为2

2. 使用欧式距离对簇进行分类，与最近的簇为一类，如上图所示，分为红蓝两类

3. 对已分类的所有数据区均值，取X/Y坐标的平均值，设为新的中心点，如上图c-d的操作

4. 重新对簇进行分类（如步骤2），如上图d-c的操作

5. 迭代直到结束。

结束迭代的方法有很多，比如收敛达到一定程度后结束迭代，如无法收敛可以设置迭代次数

问题：

1. 需要先验知识，必须给定一个簇，簇多簇少效果是截然不同的。

2. 初始簇中心点对算法影响较大，如果初始值不太好，可能对结果产生较大的影响。

3. 去噪点能力差，误差数据可能会对结果造成较大的影响。

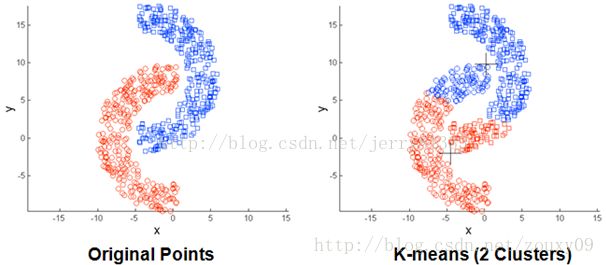
4. 仅适用于球心数据分布

5. 数据比较大时收敛比较慢

解决：

对于中心点的收敛问题，可以使用特殊的求中心点公式：

1. Minkowski Distance 公式 —— λ 可以随意取值，可以是负数，也可以是正数，或是无穷大

2. Euclidean Distance 公式 —— 也就是第一个公式 λ=2 的情况

3. CityBlock Distance 公式 —— 也就是第一个公式 λ=1 的情况

K-means ++

为了解决随机初始点不好并且不知道初始中心点数量的问题，这里可以引入K-means++。

1. 先从数据库随机挑个随机点当“种子点”。
2. 对于每个点，都计算其和最近的一个“种子点”的距离D(x)并保存在一个数组里，然后把这些距离加起来得到Sum(D(x))。
3. 然后，再取一个随机值，用权重的方式来取计算下一个“种子点”。这个算法的实现是，先取一个能落在Sum(D(x))中的随机值Random，然后用Random -= D(x)，直到其<=0，此时的点就是下一个“种子点”。
4. 重复第（2）和第（3）步直到所有的K个种子点都被选出来。
5. 进行K-Means算法。

K-modes

K-modes是K-means用在非数值集合上的一种方法，将原本K-means使用的欧式距离替换成字符间的汉明距离。

K-prototype

K-prototype是K-means与K-modes的一种集合形式，适用于数值类型与字符类型集合的数据。

1. 度量具有混合属性的方法是，数值属性采用K-means方法得到P1，分类属性采用K-modes方法P2，那么D=P1+a*P2，a是权重。如果觉得分类属性重要，则增加a，否则减少a，a=0时即只有数值属性

2. 更新一个簇的中心的方法，方法是结合K-means与K-modes的更新。

Python代码

以下基于Python 3.6，修改自http://blog.csdn.net/zouxy09/article/details/17589329这篇博客：

from numpy import *  
import time  
import matplotlib.pyplot as plt  
  
  
# calculate Euclidean distance  
def euclDistance(vector1, vector2):  
    return sqrt(sum(power(vector2 - vector1, 2)))  
  
# init centroids with random samples  
def initCentroids(dataSet, k):  
    numSamples, dim = dataSet.shape  
    centroids = zeros((k, dim))  
    for i in range(k):  
        index = int(random.uniform(0, numSamples))  
        centroids[i, :] = dataSet[index, :]  
    return centroids  
  
# k-means cluster  
def kmeans(dataSet, k):  
    numSamples = dataSet.shape[0]  
    # first column stores which cluster this sample belongs to,  
    # second column stores the error between this sample and its centroid  
    clusterAssment = mat(zeros((numSamples, 2)))  
    clusterChanged = True  
  
    ## step 1: init centroids  
    centroids = initCentroids(dataSet, k)  
  
    while clusterChanged:  
        clusterChanged = False  
        ## for each sample  
        for i in range(numSamples):  
            minDist  = 100000.0  
            minIndex = 0  
            ## for each centroid  
            ## step 2: find the centroid who is closest  
            for j in range(k):  
                distance = euclDistance(centroids[j, :], dataSet[i, :])  
                if distance < minDist:  
                    minDist  = distance  
                    minIndex = j  
              
            ## step 3: update its cluster  
            if clusterAssment[i, 0] != minIndex:  
                clusterChanged = True  
                clusterAssment[i, :] = minIndex, minDist**2  
  
        ## step 4: update centroids  
        for j in range(k):  
            pointsInCluster = dataSet[nonzero(clusterAssment[:, 0].A == j)[0]]  
            centroids[j, :] = mean(pointsInCluster, axis = 0)  
  
    print ('Congratulations, cluster complete!')  
    return centroids, clusterAssment  
  
# show your cluster only available with 2-D data  
def showCluster(dataSet, k, centroids, clusterAssment):  
    numSamples, dim = dataSet.shape  
    if dim != 2:  
        print ("Sorry! I can not draw because the dimension of your data is not 2!")  
        return 1  
  
    mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ' len(mark):  
        print ("Sorry! Your k is too large! please contact Zouxy" ) 
        return 1  
  
    # draw all samples  
    for i in range(numSamples):  
        markIndex = int(clusterAssment[i, 0])  
        plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex])  
  
    mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '

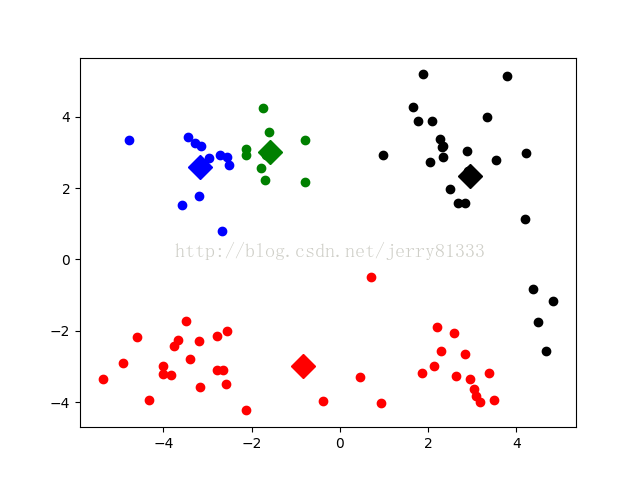
此为数据集：

1.658985    4.285136  
-3.453687   3.424321  
4.838138    -1.151539  
-5.379713   -3.362104  
0.972564    2.924086  
-3.567919   1.531611  
0.450614    -3.302219  
-3.487105   -1.724432  
2.668759    1.594842  
-3.156485   3.191137  
3.165506    -3.999838  
-2.786837   -3.099354  
4.208187    2.984927  
-2.123337   2.943366  
0.704199    -0.479481  
-0.392370   -3.963704  
2.831667    1.574018  
-0.790153   3.343144  
2.943496    -3.357075  
-3.195883   -2.283926  
2.336445    2.875106  
-1.786345   2.554248  
2.190101    -1.906020  
-3.403367   -2.778288  
1.778124    3.880832  
-1.688346   2.230267  
2.592976    -2.054368  
-4.007257   -3.207066  
2.257734    3.387564  
-2.679011   0.785119  
0.939512    -4.023563  
-3.674424   -2.261084  
2.046259    2.735279  
-3.189470   1.780269  
4.372646    -0.822248  
-2.579316   -3.497576  
1.889034    5.190400  
-0.798747   2.185588  
2.836520    -2.658556  
-3.837877   -3.253815  
2.096701    3.886007  
-2.709034   2.923887  
3.367037    -3.184789  
-2.121479   -4.232586  
2.329546    3.179764  
-3.284816   3.273099  
3.091414    -3.815232  
-3.762093   -2.432191  
3.542056    2.778832  
-1.736822   4.241041  
2.127073    -2.983680  
-4.323818   -3.938116  
3.792121    5.135768  
-4.786473   3.358547  
2.624081    -3.260715  
-4.009299   -2.978115  
2.493525    1.963710  
-2.513661   2.642162  
1.864375    -3.176309  
-3.171184   -3.572452  
2.894220    2.489128  
-2.562539   2.884438  
3.491078    -3.947487  
-2.565729   -2.012114  
3.332948    3.983102  
-1.616805   3.573188  
2.280615    -2.559444  
-2.651229   -3.103198  
2.321395    3.154987  
-1.685703   2.939697  
3.031012    -3.620252  
-4.599622   -2.185829  
4.196223    1.126677  
-2.133863   3.093686  
4.668892    -2.562705  
-2.793241   -2.149706  
2.884105    3.043438  
-2.967647   2.848696  
4.479332    -1.764772  
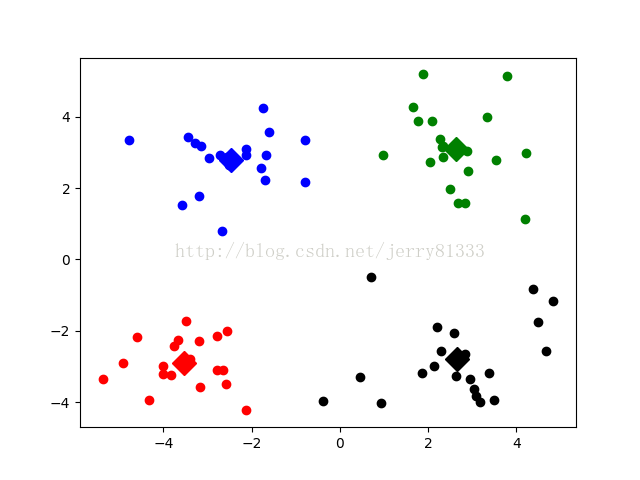
-4.905566   -2.911070  

效果图：

因为仅使用了最基础的K-means算法，并且随机初始点，因此有一定概率出现不好的聚类情况，如下图：