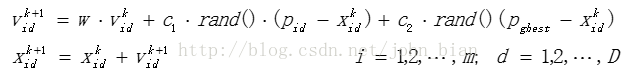粒子群算法求函数极值
粒子群算法是群智能算法中的一种,除此之外还有其他的群智能算法,如蚁群算法、猴群算法、鱼群算法等等。本文是关于粒子群算法的。所有的群智能算法都是通过模拟自然界中的生物群体的行为来解决问题的一种思想,同遗传算法一样,群智能算法的数学理论基础相对薄弱,缺乏具备普遍意义的理论性分析,算法中涉及的各种参数设置一直没有确切地理论依据,通常都是按照经验型方法确定,对具体问题和应用环境的依赖性比较大。同其他的自适应问题处理方法一样,群智能也不具备绝对的绝对的可信性,当处理突发事件时,系统的反应可能是不可测的,这在一定程度上也增加了其应用风险。
粒子群算法是通过模拟鸟群或蜂群的觅食行为来实现的一种算法思想。其基本思想是:通过群体中的个体之间的协作和信息共享来寻找最优解。
一群鸟在随机地搜索食物,在一块区域里只有一块食物,所有的鸟都不知道食物在哪儿,但是他们知道自己的当前位置距离食物有多远。我们将每一个飞行的小鸟抽象为一个无质量、无体积的粒子。每个粒子都有一个适应度(评估)函数值以模拟每只小鸟与食物的距离。每个粒子有一个速度决定它的飞行方向和距离,初始值可以随机确定。每一次单位时间的飞行之后,所有的粒子分享信息,下一步将飞向自身最佳位置(个体极值(pbest))和全局最优位置(全局极值(gbest))的加权中心。
粒子的速度和位置更新公式如下所示
其中,w称为惯性权重,c1和c2为两个正常系数,称为加速因子。将粒子的速度限制在一个最大速度之内。
从速度公式中我们可以看到粒子的速度主要由三部分组成,分别是“惯性部分”,对自身状态的信任;“认知部分”,对粒子本身的思考,即来源于自己的经验的部分;“社会部分”,粒子间的信息共享,来源于群体的其他优秀微粒的经验。
现给一个函数如下
其中m=30,0
首先是求解函数值的一个函数:
function [ z ] = thefunction( x,y )
%UNTITLED2 此处显示有关此函数的摘要
% 此处显示详细说明
z = 0;
if x>=0 && x<30
if y>=0 && y<30
z = 30*x-y;
else if y>=30 && y<=60
z = 30*y-x;
end
end
end
if x>=30 && x<=60
if y>=0 && y<=30
z = x*x-y/2;
else if y>=30 && y<=60
z = 20*y*y-500*x;
end
end
end
end下面是求解极大值的代码;
%粒子群算法求解极大值
clc,clear
vmax = 60;
w = 1;
num = 10000;
x1 = zeros(2,num);
x2 = zeros(2,num);
x3 = zeros(2,num);
x4 = zeros(2,num);
x5 = zeros(2,num);
x1(:,1) = [20; 20];
x2(:,1) = [20; 40];
x3(:,1) = [40; 20];
x4(:,1) = [40; 40];
x5(:,1) = [30; 30];
x = zeros(5,2,num);
x(1,:,1) = [20;20];
x(2,:,1) = [20;40];
x(3,:,1) = [40;20];
x(4,:,1) = [40;40];
x(5,:,1) = [30;30];
pbest = zeros(5,2,num);
pbest(1,:,1) = x(1,:,1);
pbest(2,:,1) = x(2,:,1);
pbest(3,:,1) = x(3,:,1);
pbest(4,:,1) = x(4,:,1);
pbest(5,:,1) = x(5,:,1);
gbest = zeros(2,num);
gbest(:,1) = x(1,:,1);
for i = 2:5
if thefunction(gbest(1,1),gbest(2,1))vmax
v(j,1,i) = vmax;
end
if v(j,2,i)>vmax;
v(j,2,i) = vmax;
end
x(j,:,i) = x(j,:,i-1)+v(j,:,i);
if x(j,1,i)<0
x(j,1,i) = 0;
end
if x(j,1,i)>60
x(j,1,i) = 60;
end
if x(j,2,i)<0
x(j,2,i) = 0;
end
if x(j,2,i)>60
x(j,2,i) = 60;
end
if thefunction(x(j,1,i),x(j,2,i)>thefunction(pbest(j,1,i-1),pbest(j,2,i-1)))
pbest(j,:,i) = x(j,:,i);
else
pbest(j,:,i) = pbest(j,:,i-1);
end
end
gbest(:,i) = pbest(1,:,i);
for j = 2:4
if thefunction(gbest(1,i),gbest(2,i)) x随迭代次数的变化如下
y值随迭代次数的变化如下
所以当x=60,y=60时函数取得极大值。
求解极小值的代码如下:
%粒子群算法求解极小值
clc,clear
vmax = 60;
w = 0.8;
num = 10000;
x1 = zeros(2,num);
x2 = zeros(2,num);
x3 = zeros(2,num);
x4 = zeros(2,num);
x5 = zeros(2,num);
x1(:,1) = [20; 20];
x2(:,1) = [20; 40];
x3(:,1) = [40; 20];
x4(:,1) = [40; 40];
x5(:,1) = [30; 30];
x = zeros(5,2,num);
x(1,:,1) = [20;20];
x(2,:,1) = [20;40];
x(3,:,1) = [40;20];
x(4,:,1) = [40;40];
x(5,:,1) = [30;30];
pbest = zeros(5,2,num);
pbest(1,:,1) = x(1,:,1);
pbest(2,:,1) = x(2,:,1);
pbest(3,:,1) = x(3,:,1);
pbest(4,:,1) = x(4,:,1);
pbest(5,:,1) = x(5,:,1);
gbest = zeros(2,num);
gbest(:,1) = x(1,:,1);
for i = 2:5
if thefunction(gbest(1,1),gbest(2,1))>thefunction(pbest(i,1,1),pbest(i,2,1))
gbest(:,1) = pbest(i,:,1);
end
end
v = zeros(5,2,10000);
for i = 1:5
v(i,:,1) = [1;1];
end
for i = 2:10000
for j = 1:5
v(j,:,i) = w*v(j,:,i-1)+rand(1)*(pbest(j,:,i-1)-x(j,:,i-1));
if v(j,1,i)>vmax
v(j,1,i) = vmax;
end
if v(j,2,i)>vmax;
v(j,2,i) = vmax;
end
x(j,:,i) = x(j,:,i-1)+v(j,:,i);
if x(j,1,i)<0
x(j,1,i) = 0;
end
if x(j,1,i)>60
x(j,1,i) = 60;
end
if x(j,2,i)<0
x(j,2,i) = 0;
end
if x(j,2,i)>60
x(j,2,i) = 60;
end
if thefunction(x(j,1,i),x(j,2,i)thefunction(pbest(j,1,i),pbest(j,2,i))
gbest(:,i) = pbest(j,:,i);
end
end
end
scatter(1:100,gbest(2,1:100))
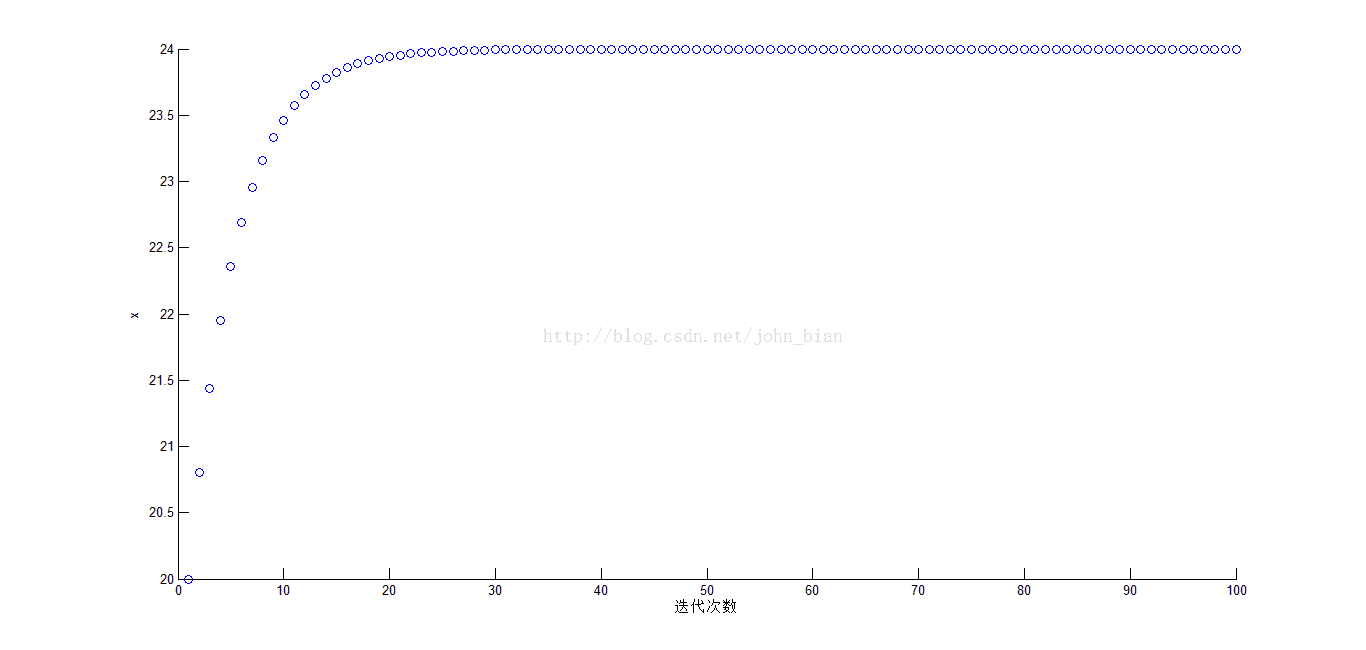
x随迭代次数的变化如下图所示
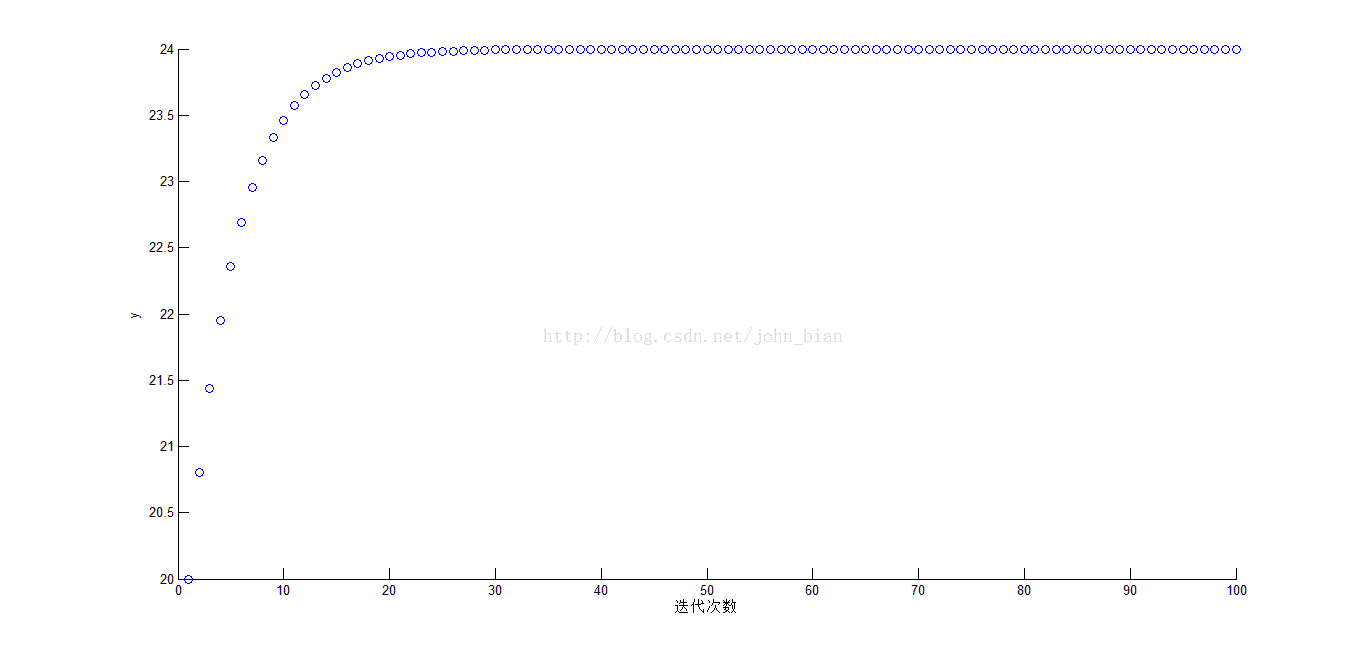
y随迭代次数的变化如下图所示
所以当x=24,y=24时函数取得极小值。