推荐系统中相似度综述与对比

本文将介绍推荐系统中用于度量相似度的几种方法，包括：余弦相似度，调整余弦相似度、欧氏距离，

以及他们之间的对比。

Reference

https://blog.csdn.net/tumantou2hao/article/details/88726531

https://blog.csdn.net/ZZh1301051836/article/details/81632712

 

1 余弦相似度 [1]

余弦距离，也称为余弦相似度，是用两个n维向量夹角的余弦值作为衡量两个个体间差异的大小的度量。（两向量的夹角越小，说明两个向量越相似）

向量，是多维空间中有方向的线段，如果两个向量的方向一致，即夹角接近零，那么这两个向量就相近。而要确定两个向量方向是否一致，这就要用到余弦定理计算向量的夹角。

余弦定理描述了三角形中任何一个夹角和三个边的关系。给定三角形的三条边，可以使用余弦定理求出三角形各个角的角度。假定三角形的三条边为a，b和c，对应的三个角为A，B和C，那么角A的余弦为：

如果将三角形的两边b和c看成是两个向量，则上述公式等价于：

其中分母表示两个向量b和c的长度，分子表示两个向量的内积。
举一个具体的例子，假如新闻X和新闻Y对应向量分别是：
x1, x2, …, x6400和
y1, y2, …, y6400
则，它们之间的余弦距离可以用它们之间夹角的余弦值来表示：

当两条新闻向量夹角余弦等于1时，这两条新闻完全重复（用这个办法可以删除爬虫所收集网页中的重复网页）；当夹角的余弦值接近于1时，两条新闻相似（可以用作文本分类）；夹角的余弦越小，两条新闻越不相关。

2 欧几里得距离 [2]

2.1 定义

欧几里得度量（euclidean metric）（也称欧氏距离），指在m维空间中两个点之间的真实距离。在二维和三维空间中的欧氏距离就是两点之间的实际距离。[2]

2.2 计算公式

2.3 在推荐系统中的应用

将两个用户（user1、user2）都评价过的n个物品（item1~n）作为维度，建立两个n维向量。那么通过用户对单一维度（即某个物品）上的评价分数组成的坐标系X（s1,s2,s3……，si）即可定位该用户在这个n维空间中的位置，那么任意两个位置之间的距离Distance(X,Y)（即：欧式距离）就能在一定程度上反应了两用户兴趣的相似程度。

下图是二维空间中6位用户对Snakes 和 Dupree 这两个物品评价的直观体现：

就其意义而言，欧氏距离越小，两个用户相似度就越大，欧氏距离越大，两个用户相似度就越小。
在日常使用中，一般习惯于将相似度与1类比，相似度在数值上反映为0<=Similarity(X,y)<=1，越接近1，相似度越高；那么我们在使用欧几里得距离时，可以通过 1/（1+Distance(X,Y)）来贯彻上一理念。（通过这一分式的变化，便可以实现距离越远，相似度越趋近于0，距离越近，相似度越趋近于1）

2.4 注意事项

a.因为计算是基于各维度特征的绝对数值，所以欧氏度量需要保证各维度指标在相同的*刻度级别，比如对身高（cm）和体重（kg）两个单位不同的指标使用欧式距离可能使结果失效。

b.欧几里得距离是数据上的直观体现，看似简单，但在处理一些受主观影响很大的评分数据时，效果则不太明显；比如，U1对Item1,Item2 分别给出了2分，4分的评价;U2 则给出了4分，8分的评分。通过分数可以大概看出，两位用户褒Item2 ,贬Item1，也许是性格问题，U1 打分更保守点，评分偏低，U2则更粗放一点，分值略高。在逻辑上，是可以给出两用户兴趣相似度很高的结论。如果此时用欧式距离来处理，得到的结果却不尽如人意。即评价者的评价相对于平均水平偏离很大的时候欧几里德距离不能很好的揭示出真实的相似度。

2.5 代码实现

#得到两者共同评分项
defGetSameItem(UL,p1,p2):
        si = {}
        for item in UL[p1]:
               if item in UL[p2]:
                       si[item] = 1
        return si

#欧几里得相似度算法
defEuclidSimilarity(UL,p1,p2):
        si = GetSameItem(UL,p1,p2)
        if len(si) == 0:
               return 0
        sum_of_squares = sum([pow(UL[p1][item] -UL[p2][item] , 2) for item in si])
        return 1/(1+math.sqrt(sum_of_squares))

•  

3 余弦距离和欧氏距离的对比

从上图可以看出，余弦距离使用两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比欧氏距离，余弦距离更加注重两个向量在方向上的差异。

从上图可以看出，欧氏距离衡量的是空间各点的绝对距离，跟各个点所在的位置坐标直接相关；而余弦距离衡量的是空间向量的夹角，更加体现在方向上的差异，而不是位置。如果保持A点位置不变，B点朝原方向远离坐标轴原点，那么这个时候余弦距离 clip_image011 是保持不变的（因为夹角没有发生变化），而A、B两点的距离显然在发生改变，这就是欧氏距离和余弦距离的不同之处。

欧氏距离和余弦距离各自有不同的计算方式和衡量特征，因此它们适用于不同的数据分析模型：
（1）欧氏距离能够体现个体数值特征的绝对差异，所以更多的用于需要从维度的数值大小中体现差异的分析，如使用用户行为指标分析用户价值的相似度或差异。
（2）余弦距离更多的是从方向上区分差异，而对绝对的数值不敏感，更多的用于使用用户对内容评分来区分兴趣的相似度和差异，同时修正了用户间可能存在的度量标准不统一的问题（因为余弦距离对绝对数值不敏感）。

4 调整余弦相似度算法（Adjusted Cosine Similarity）

余弦相似度更多的是从方向上区分差异，而对绝对的数值不敏感，因此没法衡量每个维度上数值的差异，会导致这样一种情况：

用户对内容评分，按5分制，X和Y两个用户对两个内容的评分分别为（1,2）和（4,5），使用余弦相似度得到的结果是0.98，两者极为相似。但从评分上看X似乎不喜欢2这个 内容，而Y则比较喜欢，余弦相似度对数值的不敏感导致了结果的误差，需要修正这种不合理性就出现了调整余弦相似度，即所有维度上的数值都减去一个均值，比如X和Y的评分均值都是3，那么调整后为（-2，-1）和（1,2），再用余弦相似度计算，得到-0.8，相似度为负值并且差异不小，但显然更加符合现实。

那么是否可以在（用户-商品-行为数值）矩阵的基础上使用调整余弦相似度计算呢？从算法原理分析，复杂度虽然增加了，但是应该比普通余弦夹角算法要强。

 

对比

传统的推荐算法（如协同过滤、基于物品的推荐等）采用的相似度计算公式主要有：余弦夹角、欧氏距离、杰卡德系数和皮尔森相关系数等，那么这些方法具体有哪些差异，在推荐算法中该如何选择，下面将着重基于这两个方面进行分析说明。

1）余弦夹角 和 欧氏距离

在向量空间中，任意两点（设为A、B）间的关系可通过余弦夹角和欧式距离来衡量，其中余弦夹角衡量的是A和B在空间方向上的差异，欧式距离是A和B在空间位置上的差异。因此，两者的差异主要体现：
（1）欧氏距离从向量间的绝对距离区分差异，计算得到的相似度值对向量各个维度内的数值特征非常敏感，而余弦夹角从向量间的方向夹角区分差异，对向量各个维度内的数值特征不敏感；
（2）余弦夹角公式对向量进行了归一化处理，解决了向量个体间存在度量标准不统一问题产生的计算偏差；
（3）余弦夹角的值域区间为[-1,1]，相对于欧式距离的值域范围[0,正无穷大],能够很好的对向量间的相似度值进行了量化。
因此，在推荐系统场景下，推荐算法大都采用余弦夹角进行用户（或物品）的相似度计算。当然，欧氏距离能够体现个体数值特征的绝对差异，一般用于需要从维度的数值大小中体现差异的相关度分析（如从用户行为指标分析用户价值的相似度或差异）。

 

2）余弦夹角 和 皮尔森相关系数

皮尔森相关系数是用于衡量任意两个变量间线性相关程度的统计量，系数值越大相关性越强，值域范围为[-1,1]。在推荐系统的用户（或物品）间相似度计算过程中，余弦夹角和皮尔森相关系数的定义公式相似，具体如下：
（1）余弦夹角公式：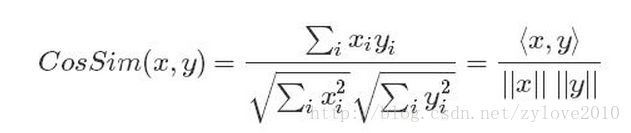 
（2）皮尔森相关系数公式：

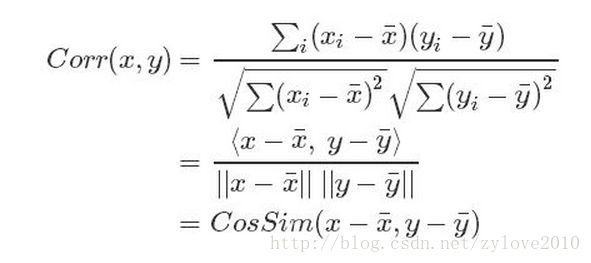
从两者的定义公式可知，相对于余弦夹角公式，皮尔森相关系数公式对变量进行了均值化（或去中心化）处理，其好处是减少变量个体的数值差异对变量间相似度的影响。举个例子，用户A习惯对所有物品的评分范围为[1,3]，而用户B习惯对所有物品的评分范围为[3,5]，因各自评分数值标准的差异，采用余弦夹角公式计算两者的相似度比较低，但实际上两者的相似度是很高的。因此，在实际的推荐系统中，大都采用皮尔森相关系数公式或者下面的修正余弦夹角公式。

(3）修正的余弦夹角公式（以计算物品i和j的相似性为例）：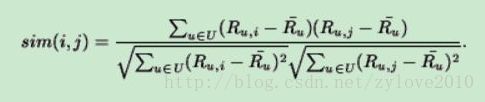

其中i,j代表两个物品，u代表用户，Ru,i代表用户u对物品i的评分，Ru￣代表用户u对所有物品评分的均值，对比发现，修正的余弦夹角公式与皮尔森相关系数公式非常相似。

(4）皮尔森相关系数公式（以计算物品i和j的相似性为例）：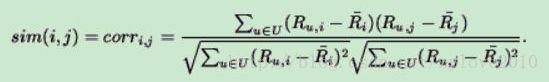

Ri 表示第i个物品打分的平均值

两者的差异主要在评分均值的计算方式上，修正的余弦夹角计算的是用户的评分均值，皮尔森相关系数计算的是物品的评分均值。可以推断，在计算用户i和j的相似性时，两者的计算公式是完全一致的。

 

3）余弦夹角 与 杰卡德系数

杰卡德系数是衡量两个集合间相似性的常用公式，其定义如下：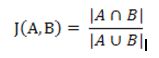 
从杰卡德系数的计算公式可知，其限制了A和B的取值范围（0或1），当然，将A或B进行向量化后即可进行余弦夹角公式进行计算，相对余弦夹角，杰卡德系数计算公式的优势是其计算复杂度不高。因此在推荐系统中，若样本的特征值为二值（0或1），大都采用杰卡德系数或者其推广公式，比如在基于物品的协同过滤推荐算法中计算物品间的相似度。