AOE网络-关键路径
拓扑排序的另一个应用就是关键路径的问题,关键路径对应的是另一种网络:AOE网络。先回顾下拓扑排序中讲到的AOV网络,AOV网络即“Activity On Vertex”,即图上每一个顶点表示的是一个事件或者说一个活动,而顶点之间的有向边则表示这两个活动发生的先后顺序。
在关键路径这个问题中,AOE网络指的是“Activity On Edge”,即图上的每一条边表示的是一个活动,顶点作为各个“入度边事件”的汇集点,意思是,某个顶点,当所有的“入度边事件”的活动全部完成后,才开始进行该顶点的“出度边事件”。在AOE网络中只有一个入度为零的点,称作源头顶点,和一个出度为零的目的顶点。AOE网络通常用来安排一些项目的工序。
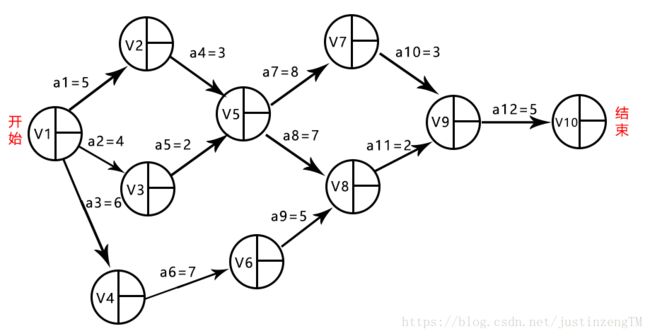
上图表示的就是AOE网络中的,有向边上方表示该活动的持续时间,也就是完成该活动要多长时间,有向边下方表示该活动的机动时间,机动时间是什么呢,下面等拿例子来讲解时再解释。顶点里又分为三部分,一部分是存放顶点的编号,另外两部分分别存放活动的最早完成时间(即到达该点用时最短),和最晚完成时间(即到达该点用时最长)。
下面根据一个具体的例子来看到底什么是AOE网络和关键路径:
在下面的有向无环图中,V1是源头顶点(即开始点),到V10结束,每一条边代表一个活动,有向边的方向表示活动完成后到达哪一个汇集点。有向边上方表示的是活动完成所需要的时间(也是持续时间)。假设活动a7和a8想要开始,那么必须等到活动a4和a5都完成后,a7和a8才能开始。
还有一种更复杂的情况是:如果活动a7和a8要开始,必须要等活动a4、a5和a6都完成后,才能开始a7和a8活动(因为在AOE网络中有些活动是可以并行地进行的)。这样的情况怎么办?我们不可以把V5和V6顶点连接起来,为什么?因为我们看a9这个活动,它的开始与否和活动a4,a5均无关系,活动a9只需等待活动a6完成他就可以开始了,所以如果我们把V5和V6顶点连接起来,是不行的。那要怎么办?方法是用一个无向虚线(标记线)把V5和V6连接,边上的权值设为0,如图:
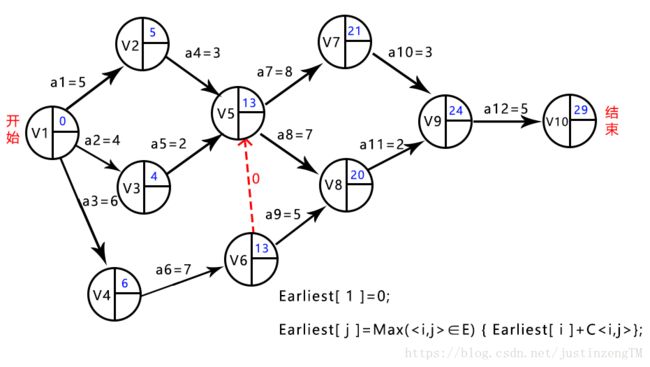
接着根据这个有向无环图,我们看看从开始到结束整个工程活动需要的最短时间是多少?答案是从开始点出发到完成点的最长路径的长度(这里的最长路径长度指的是路径上各个活动持续时间之和,不是指路径上边的数目)。从开始点到结束点的最长路径就叫做关键路径。从开始结点V1开始,它的最早完成时间自然是0了,然后到V2结点,V2结点的最早完成时间是5,同理V3结点最早需要4天完成,V4结点最早需要6天完成。
接着到下一组,从V4到V6顶点,活动a6需要7天,所以V6上填上6+7=13,也就是说到达V6需要最早完成时间是13天。对于V5这个顶点,它的完成时间有三个,分别是5+3=8,4+2=6和13+0=13。这里我们就要选一个最大的填进去,因为V5的“出度边事件”要进行,也就是活动a7和a8要开始的话,必须等齐a4,a5和a6三个活动结束后才能开始,所以在a4、a5和a6中选一个完成时间最大的,就能确保三个活动都能完成。
到这里我们就知道程序大概要怎么写了:
首先我们需要一个Earliest[ ]数组来存放每一个顶点的最早完成时间,Earliest[ 1 ]=0代表的就是开始结点V1的最早完成时间是0,对于图中每一个顶点对
按照这个思路,我们可以把图里接下来的顶点的完成时间都填好:
到最后V10结束结点等于29,也就是说整个图的所有活动的最短完成时间是29天。
最后到来看看这个图中活动的机动时间,什么是机动时间呢,就是指图中这些活动中,有哪些活动是一直进行下去的,没有休息时间的。例如活动a10需要3天完成,而获得a11需要2天,则a11有1天的休息时间等待a10完成,a11的这一天休息时间就是所谓的“机动时间”。
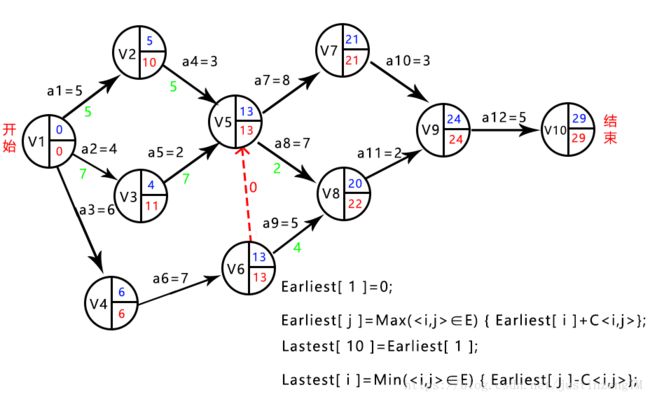
我们用e(i)来表示活动ai的最早完成时间,l(i)表示ai的最迟开始时间,机动时间要怎么算呢?看图来说,我们从结束结点开始倒推,在保证整个工期都不推迟的情况下,也就是第29天开始,反推回去,看结点V9,活动a12需要5天,就是说在保证整个工期能在29天完成的情况下,V9的最晚开始时间(也就是最迟完成时间)是29-5=24,就是说活动a12最迟必须在第24天就要开始工作了。V7结点和V8结点同理,V7结点最迟必须在第24-3=21天就开始工作,V8结点最迟必须在第24-2=22天开始就工作。
接着看V5结点,从V8倒推到V5,就是22-7=15,a8活动最迟第15天就要开始工作。而从V7倒推到V5的话,21-8=13,a8活动最迟第13天就要开始工作,这里出现两个不同的值,怎么选?答案是选最小值13,因为如果选择第15天开工,那么对于活动a7来说,就延迟了两天开工了,这样就不能保证后面能在29天内完成整个工程,所以遇到两种不同的最晚开始时间时,我们要选最小的,这样才能保证整个工期不被延误。
同样的,看V6结点,从V8结点倒推到V6结点,22-5=17天,也就是活动a9的最迟开始时间可以是在第17天时才开工?答案是不行的,因为V6结点和V5结点有个虚线连着呢,V6结点,也就是活动a9的最迟开始时间同样是13天。
从这里就可以看出我们的求机动时间的倒推时的推断是,需要一个Latest[ ]数组存放每一个结点的最迟开始时间,一开始初始化结束结点的Latest[ 10 ]=Earliest[ 1 ],也就是29。然后倒推时,Latest[ i ]就等于Last[ j ]-C
按照这个推断,就可以把剩下的顶点的最晚开始时间都算出来:
V1顶点有三种选择,V2到V1等于5,V3到V1等于7,V4到V1等于0,因为我们要选择最小值,所以V1填上0。
最后来看看每个结点的机动时间,我们从头开始看,活动a1需要工作5天才完成,到达V2结点中,最迟开始时间是10,也就是说活动a4最迟在第10天开始工作都不会耽误整个工期,而a1从第0天开始只需工作5天就能完成,所以活动a1的机动时间就是10-0-5=5,五天。活动a2最迟在第11天开始工作就可以了,而活动a2只需要4天就可以完成,所以a2的机动时间是11-0-4=7,七天。活动a3等于6-0-6=0,所以活动a3机动时间等于0,也就是说活动a3完成后就要开始下一个活动了,中间没有“休息时间”。
同理可看出,a4的机动时间是13-5-3=5。a5的机动时间是13-4-2=9。a6是13-6-7=0。这样我们就可以把所有的机动时间都算出来:
我们假设用e(i)表示活动ai的最早开始时间,用l(i)表示活动的最迟开始时间,那么两者之差l(i)-e(i)表示活动ai的机动时间,把e(i)=l(i)的活动我们称为“关键活动”。关键路径上所有的活动都是关键活动。回到关键路径的问题,关键路径有可能不止一条。所以找出关键路径即找出路径上所有活动都是关键活动的路径即可。
/*拓扑排序*/
bool TopSort(ListGraphNode MyGraph, Vertex TopOrder[])
{
/*TopOrder[]数组用来顺序存储排序后的顶点的下标*/
/*在拓扑排序完成后直接顺序输出TopOrder[]里的元*/
/*素就能得到拓扑排序序列*/
int i;
int Indegree[MaxVertex], cnt;/*Indegree数组是图中顶点的入度,cnt是计数器*/
Vertex V;/*扫描V顶点的邻接点*/
PtrlPointNode W; /*邻接表方式表示图*/
Queue PtrQ=Start();
for (i=0; iData[i]=-1;
}
/*初始化入度数组*/
for (V=0; Vnumv; V++) {
Indegree[V]=0;
}
/*遍历图,得到图中入各顶点的入度情况并存入Indegree数组中*/
for (V=0; Vnumv; V++) {
for (W=MyGraph->PL[V].HeadEdge; W; W=W->Next) {
Indegree[W->Tail]++;
}
}
/*将所有入度为0的顶点入列*/
for (V=0; Vnumv; V++) {
if (Indegree[V]==0) {
Push(PtrQ, V);
}
}
/*开始拓扑排序*/
cnt=0; /*初始化计数器为0*/
while (PtrQ->End!=PtrQ->Head) {
V=Delete(PtrQ);/*出列一个入度为0的顶点*/
TopOrder[cnt++]=V;/*拓扑排序数组里记录该出列顶点的下标*/
/*遍历对于V的每个邻接点W->PL.HeadEdge.index*/
for (W=MyGraph->PL[V].HeadEdge; W; W=W->Next) {
/*若删除V能使该顶点的入度为0*/
if (--Indegree[W->Tail]==0) {
/*把该顶点入列*/
Push(PtrQ, W->Tail);
}
/*同时更新Earliest数组的值*/
if ((Earliest[V]+W->Weight)>Earliest[W->Head]) {
Earliest[W->Tail]=Earliest[V]+W->Weight;
}
}
}
/*最后判断*/
if (cnt!=MyGraph->numv) {
return false;/*说明该图里有回路,返回false*/
} else {
return true;
}
} 在拓扑排序过程中,我们就同时更新Earliest数组,把每一个顶点的最早完成时间填入到数组中。
/*关键路径*/
bool CriticalPath(ListGraphNode MyGraph, int TopOrder[])
{
int k, ee, el;
PtrlPointNode W;
Queue List=Start();
/*得到后面逆序用*/
for (k=0; knumv ; k++) {
Push(List, TopOrder[k]);
}
/*初始化Lastest数组*/
for (k=0; knumv; k++) {
Lastest[k]=Earliest[MyGraph->numv-1];
}
/*开始关键路径*/
while (List->End!=List->Head) {
k=Delete(List);/*出列一个入度为0的顶点*/
/*遍历对于V的每个邻接点W->PL.HeadEdge.index*/
for (W=MyGraph->PL[k].HeadEdge; W; W=W->Next) {
if (Lastest[k]>(Lastest[W->Tail]-W->Weight)) {
Lastest[k]=Lastest[W->Tail]-W->Weight;
}
}
//printf("关键路径为:");
for (k=0; knumv; k++) {
W=MyGraph->PL[k].HeadEdge;
while (W) {
ee=Earliest[k];
el=Lastest[W->Tail]-W->Weight;
if (ee==el) {
/*两值相等说明它们是关键活动*/
printf("v%d--v%d=%d", MyGraph->PL[k].HeadEdge->Tail, MyGraph->PL[W->Head].HeadEdge->Tail, W->Weight);
}
W=W->Next;
}
}
}
} 在关键路径的计算过程中再逆序计算出最迟开始时间即可。
完整代码在个人代码云:
https://gitee.com/justinzeng/codes/9jbqdrhgn8xl31y6vsw2u75