浅淡深度学习的发机机——张量计算
浅淡深度学习的发机机——张量计算
张量计算是个看似陌生,实际上很常用的事物,它包括图形渲染的透明度混合、图像处理的滤镜、数学计算中的矩阵乘法、卷积等等,是图形引擎、图像算法、机器学习以及深度学习的基础。如何进行高效的张量计算,是OpenCV之类的图像库、OpenBlas / Eigen之类的高性能计算库以及MNN之类的深度学习推理引擎要解决的核心问题。
本文主要以端侧深度学习推理引擎MNN为示例,谈一下张量计算及主要优化策略。
相关链接
https://github.com/alibaba/MNN
1. 概念说明
本节对张量计算做一些概念上的科普,熟悉Tensorflow 或者其他深度学习推理引擎的可以跳过本节。
1.1 张量
张量(英文Tensor)是标量、矢量、矩阵等概念的总称与拓展,是机器学习领域的基础数据结构。
我们这里不讨论数学意义上的张量,只考虑程序中的实现。程序中的张量是一个多维数组的数据结构,示例如下:
#define MAX_DIM 6
struct Tensor {
// 维度信息
size_t dim[MAX_DIM];
uint8_t num_dim;
// 数据信息
float* data;
size_t num_data;
};
0维张量,就是一个数。1维张量等同于一个向量。2维张量对应一个矩阵。3维张量则是一个立方体。
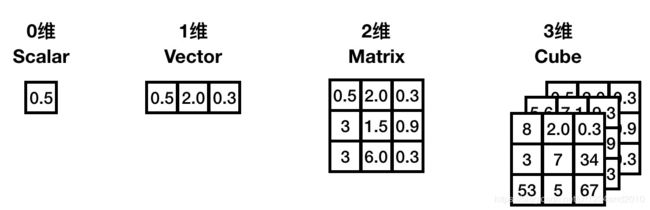
1.2 张量计算
张量集到张量集的映射称为张量计算。用编程语言来说,输入是若干张量,输出也是若干个张量,并且无副作用(参考函数式编程)的函数称之为张量计算。
由示例程序可以看出,张量有 “维度” 和 “数据” 两个组成要素,张量计算,也就包含维度与数据这两个组成要素的处理。
比如矩阵乘法C = MatMul(A, B),首先是根据输入的两个张量A, B确定C的维度,然后根据A和B的数据再去计算C的数据。具体一些可参考下面的代码:
Tensor* MatMul(Tensor* A, Tensor* B) {
Tensor* C = new Tensor;
// 计算维度
C->num_dim = 2;
C->dim[0] = A->dim[0];
C->dim[1] = B->dim[1];
// 分配内存
C->data = malloc(C->dim[0]*C->dim[1]*sizeof(float));
// 计算数据
Matrix::multi(C, A, B);
return C;
}
1.3 计算图
在深度学习领域,一个模型是由一系列的张量计算与常量组合而得的计算图,每一次张量计算称为一个算子(Op)。
比如手写数字识别的Mnist模型:
class Mnist:
def __init__(self):
self.w0, self.w1, self.w2, self.w3 = LoadWeight()
def forward(self, x):
x = Conv(x, self.w0)
x = Pool(x)
x = Conv(x, self.w1)
x = Pool(x)
x = InnerProduct(x, self.w2)
x = Relu(x)
x = InnerProduct(x, self.w3)
x = Softmax(x)
return x
它由 8个算子组成,分别是 Conv -> Pool -> Conv -> Pool -> InnerProduct->Relu->InnerProduct->Softmax
计算图涵盖了一系列的算子,最坏情况下,它的计算时间是各算子时间之合。但我们可以对计算图进行依赖分析,在资源管理、计算调度、冗余清除等方面做文章,使计算图的计算时间小于这个总合。
2. 张量计算的特点
2.1 变化的运算量
每种算子都是对一批数据进行计算,其运算量不仅取决于算子本身,也取决于数据本身的维度信息。
以下是一些常见算子的运算量的分析
| 算子 | 参数 | 输入维度 | 输出维度 | 运算量 |
|---|---|---|---|---|
| Conv | c o , k h , k w c_o, k_h, k_w co,kh,kw | ( n , c i , h , w ) (n, c_i, h,w) (n,ci,h,w) | ( n , c o , h , w ) (n, c_o, h,w) (n,co,h,w) | n c o c i h w k h k w nc_oc_ihwk_hk_w ncocihwkhkw |
| ConvDw | k h , k w k_h, k_w kh,kw | ( n , c , h , w ) (n, c, h,w) (n,c,h,w) | ( n , c , h , w ) (n, c, h,w) (n,c,h,w) | n c h w k h k w nchwk_hk_w nchwkhkw |
| MatMul | ( h i , w ) , ( w , w o ) (h_i, w), (w, w_o) (hi,w),(w,wo) | ( h i , w o ) (h_i, w_o) (hi,wo) | h i w w o h_iww_o hiwwo | |
| MatAdd | ( h , w ) , ( h , w ) (h, w), (h, w) (h,w),(h,w) | ( h , w ) (h, w) (h,w) | h w hw hw | |
| MatSub | ( h , w ) , ( h , w ) (h, w), (h, w) (h,w),(h,w) | ( h , w ) (h, w) (h,w) | h w hw hw | |
| Resize | f = 2 f=2 f=2, Bilinear | ( n , c , h , w ) (n, c, h, w) (n,c,h,w) | ( n , c , 2 h , 2 w ) (n, c, 2h, 2w) (n,c,2h,2w) | 16 n c h w 16nchw 16nchw |
| Resize | f = 0.5 f=0.5 f=0.5, Bilinear | ( n , c , h , w ) (n, c, h, w) (n,c,h,w) | ( n , c , 0.5 h , 0.5 w ) (n, c, 0.5h, 0.5w) (n,c,0.5h,0.5w) | n c h w nchw nchw |
| Resize | f = 2 f=2 f=2, Nearest | ( n , c , h , w ) (n, c, h, w) (n,c,h,w) | ( n , c , 2 h , 2 w ) (n, c, 2h, 2w) (n,c,2h,2w) | 4 n c h w 4nchw 4nchw |
由于这一性质,张量计算的耗时随着输入的变大而上升。我们在做性能分析时,不能一刀切地去说一个算子是不是耗时的,要具体地结合维度信息去判断。比如Conv(卷积算子)一般情况下比较耗时,但如果它的输入维度比较小,就很可能不如后面的一个Resize耗时多。
2.2 校验困难与误差容忍
张量计算的结果是一个庞大的数组,比如一个图像算法,输入输出均是 400 x 300 像素的RGB图像,那么它的输出数据量就是 400 x 300 x 3 = 360000 400x300x3 = 360000 400x300x3=360000,这么大的数据量我们很难人工去确认是否正确,有参考输出时,可以用统计学的一些方法,编程序判断。没有参考输出的情况,比如图像滤镜,只能人肉眼去看图像。
大部分张量计算,即便是最简单的矩阵相加,不同的计算顺序,不同的硬件指令集也可能导致计算结果有非常小的偏差。在实际的应用中,我们往往没有必要要求计算结果和标准输出完全一致,如下面两幅图像,两者像素值均存在一定偏差,但不仔细看基本分辨不出。


由于实际应用中对张量计算的结果有一定的误差容忍,我们可以采用有一定误差的优化方案,典型的就是定点计算,将原先浮点计算等效替换为整型计算。
2.3 形实无关
对常用算子而言,维度的计算仅由输入张量的维度与算子信息确定,因此可以先计算维度信息(“形”),再计算内容(“实”)。具体到一个张量计算图来说,就是先计算图中所有张量的维度,再去算各张量的内容。
一般而言,维度信息确定下来后,就能确定分配的内存大小和该算子所需要采用的最优计算流程,而很多情况下内容在不断变化,而维度信息是相对稳定的,利用这一特性,我们可以做优化,减少运行时的耗时。
并非所有算子都有这个性质,比如unique算子需要从输入张量中取互不相同的元素出来组成输出张量,就无法单从输入维度计算维度信息,对于这些情况需要特别处理。
2.4 "复杂"的优化
张量计算很多情况下需要适当添加计算步骤来加速,使得程序变得复杂而难懂。
2.4.1 普通程序的优化
对普通程序而言,性能优化是一个使代码变"简洁"的过程,删除掉冗余计算之后,性能肯定比之前好,代码看上去也更舒服。
例如:
void lower1(char *s){
long i;
for(i = 0; i < strlen(s); i++){
if(s[i] >= 'A' && s[i] <= 'Z'){
s[i] -= ('A' - 'a');
}
}
}
strlen(s) 每次循环都计算,可以放到循环外面。优化后:
void lower1(char *s){
long i;
long sLength = strlen(s);
for(i = 0; i < sLength; i++){
if(s[i] >= 'A' && s[i] <= 'Z'){
s[i] -= ('A' - 'a');
}
}
}
2.4.2 优化示例:两种矩阵乘法
我们以两种矩阵乘法为例,来看张量计算的优化。
简易版本V1
// 矩阵乘法 v1
void Matrix::multi(Tensor* C, const Tensor* A, const Tensor* B) {
const auto a = A->host();
const auto b = B->host();
auto c = C->host();
const int h = A->length(0);
const int k = A->length(1);
const int w = B->length(1);
const int aw = A->stride(0);
const int bw = B->stride(0);
const int cw = C->stride(0);
MNN_ASSERT(k == B->length(0));
for (int y=0; y < h; ++y) {
const auto aLine = a + y * aw;
auto cLine = c + y * cw;
for (int x=0; x < w; ++x) {
auto bColumn = b + x;
float sum = 0.0f;
for (int i = 0; i < k; ++i) {
sum += aLine[i] * bColumn[i * bw];
}
cLine[x] = sum;
}
}
}
复杂版本V2
具体代码参见
https://github.com/alibaba/MNN/blob/master/source/backend/cpu/CPUMatMul.cpp
// 矩阵乘法 V2 (一部分)
const Tensor* A = inputs[0];
const Tensor* B = inputs[1];
auto APtr = A->host();
auto BPtr = B->host();
Tensor* C = outputs[0];
auto CPtr = C->host();
auto w0 = inputs[0]->length(1);
auto h0 = inputs[0]->length(0);
mFunction.clear();
auto e = C->length(0);
auto h = C->length(1);
auto l = w0;
std::shared_ptr AT(Tensor::createDevice({UP_DIV(l, 4), e, 4}));
std::shared_ptr BT(Tensor::createDevice({UP_DIV(h, 4), UP_DIV(l, 4), 16}));
std::shared_ptr CT(Tensor::createDevice({UP_DIV(h, 4), e, 4}));
std::shared_ptr BTemp;
if (l % 4 != 0) {
BTemp.reset(Tensor::createDevice({UP_DIV(h, 4), l, 4}));
auto res = backend()->onAcquireBuffer(BTemp.get(), Backend::DYNAMIC);
if (!res) {
return OUT_OF_MEMORY;
}
}
auto res = backend()->onAcquireBuffer(BT.get(), Backend::DYNAMIC);
if (!res) {
return OUT_OF_MEMORY;
}
auto BTPtr = BT->host();
float* BTempPtr = BTPtr;
if(l % 4 != 0) {
BTempPtr = BTemp->host();
}
mFunction.emplace_back([BPtr, BTempPtr, l, h] {
MNNTensorConvertNHWCToNC4HW4(BTempPtr, BPtr, l, h);
});
if (l % 4 != 0) {
mFunction.emplace_back([BTPtr, BTempPtr, l, h] {
auto hC4 = UP_DIV(h, 4);
auto lC4 = UP_DIV(l, 4);
for (int y=0; yonReleaseBuffer(BTemp.get(), Backend::DYNAMIC);
}
res = backend()->onAcquireBuffer(AT.get(), Backend::DYNAMIC);
res = res && backend()->onAcquireBuffer(CT.get(), Backend::DYNAMIC);
if (!res) {
return OUT_OF_MEMORY;
}
auto ATPtr = AT->host();
mFunction.emplace_back([ATPtr, APtr, e, l]() {
MNNTensorConvertNHWCToNC4HW4(ATPtr, APtr, e, l);
});
std::shared_ptr computor(new StrassenMatrixComputor(backend()));
auto code = computor->onEncode({AT.get(), BT.get()}, {CT.get()});
if (NO_ERROR != code) {
return code;
}
auto CTPtr = CT->host();
mFunction.emplace_back([computor, CPtr, CTPtr, e, h]() {
computor->onExecute();
MNNTensorConvertNC4HW4ToNHWC(CPtr, CTPtr, e, h);
});
backend()->onReleaseBuffer(AT.get(), Backend::DYNAMIC);
backend()->onReleaseBuffer(BT.get(), Backend::DYNAMIC);
backend()->onReleaseBuffer(CT.get(), Backend::DYNAMIC);
//限于篇幅,这里只展示一部分代码,实际还有另外一大半就不展示了。
初看上去,v2版本流程比v1复杂多了。但同样单线程运行,v2版本大部分情况下速度是v1的10倍。
由于张量计算的优化是“复杂”的,针对单独张量计算函数,我们不能以将像传统程序优化一样去找冗余并清理,正确的方式请看下节。
3. 张量计算的优化
3.1 优化就是“修路”
以城市交通建设举例说明一下张量计算优化的基本思路。
比如下图,魏博下属有魏州、相州、博州、贝州、澶州,范阳下属有幽州、妫州、易州、定州、恒州。现在要让魏博的人民到范阳更方便,应该怎么做呢?
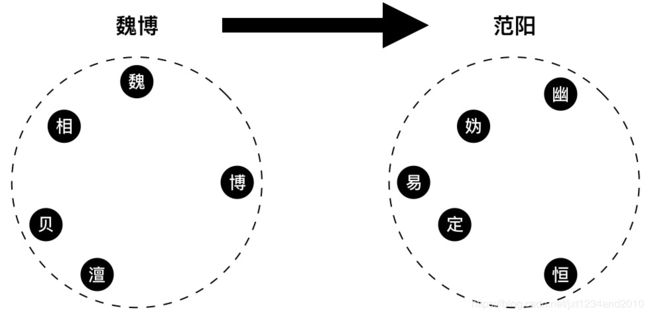
我们可以每两个州都修一条路,但这样需要25条路,成本高昂。现实中的我们的解决方案一般是这样的:
1、建一条高速路,起点站为S,终点站为D。
2、魏博各州与S连通。
3、范阳各州与D连通。

这样做的好处在于:
1、保证各州居民均能较快地到达。
2、集资打造一条高速路就可以,成本较低。
缺点在于,有些相邻比较近的州要绕远路(如图上的博州到易州)。
张量计算的优化就类似上面这个"修路"的过程,设计一系列高速计算模块,然后原始的计算转化为高速计算模块可解决的问题。
3.2 修高速——设计高性能计算模块
高性能的来源第一部分是硬件层面,在开发者层面无法参与,但需要深入了解。

第二部分是软件层面,主要分成三类策略:
第一类是相对固定的计算套路,比如汇编排列技巧、SIMD使用技巧等、GPU的调度技巧等等,这些套路需要举一反三,应用到自己的代码中。
第二类是内存访问与并发设计,有较简单的针对硬件特性的引用(比如GPU加速在高通GPU上用Image而不是用Buffer存储),也需要反复试验调试,在并行度与缓存友好中取折中的Schedule过程。
第三类是张量计算优化算法,如 Winograd 卷积计算,Strassen 矩阵乘,这些算法限定于固定的某类张量计算,但可以结合第一、二类策略广泛应用于不同的硬件上。
“修高速”是优化过程中最为重要与困难的任务,极其考验研发人员的智商与耐力。近些年来,多面体模型编译技术得到了不少发展,并以 Halide / TVM 知名度最广,这种技术可以自动地产生“高速路”,但性能与人们手工设计的仍然有差距,并且要达到较好的性能,人工且入的成本目前也不低。
3.3 连接高速——原始计算与高性能计算模块之间的转换
类似于高速路搭完之后,我们需要将居民点与高速连接,由于软件层面前两类策略的实施,高性能计算需要一些触发条件,或者称入口,随着所使用的具体硬件而不同,比如:
(1)ARM的 SIMD 运算浮点矩阵乘法要求把矩阵重排为一系列 (1, 4), (4, 4) 的小块
(2)ARMv8.2 的 SDOT 指令计算要求把矩阵重排为(4, 4), (4, 4)的小块
(3)分块后,需要申请若干缓存,以便逐块复制数据与计算
(4)使用 GPU 加速,需要创建 Kernel / Buffer,并上传数据到显存中
在高性能计算完成后,其产生的数据往往也不便于用户直接使用,需要作一些转换,使之用户可见;另外,在高性能计算过程产生的一些缓存也需要清理,这类似于一个下高速的过程,对应上文“上高速”的例子,分别的“下高速”操作为:
(1)将重排成 (1, 4) 小块的矩阵辅平
(2)将重排成 (4, 4) 小块的矩阵辅平
(3)销毁缓存
(4)将显存中的数据复制出来,销毁之前创建的Kernel/Buffer 对象。
3.4 优化方案实践——矩阵乘法
这里以上一节的矩阵乘法为例说明一个完整的张量计算优化方案。回到上节矩阵乘法的V2版本,那段复杂的代码是按如下流程编写的:
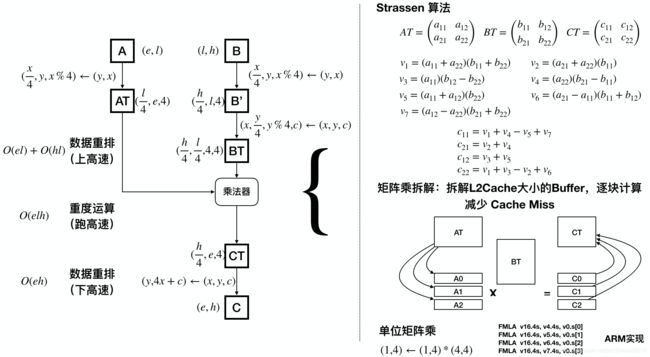
首先把 A , B 分别转到适宜计算的数据布局AT和BT,然后执行该布局下的矩阵计算,其中包含Strassen分解,分块,汇编等具体优化手段,最后把计算完成的矩阵CT转回原始的数据布局C。
这样我们付出 O ( e l ) + O ( e h ) + O ( l h ) O(el) + O(eh) + O(lh) O(el)+O(eh)+O(lh)的布局转换代价,换来核心计算 O ( e l h ) O(elh) O(elh)的数倍性能提升。
可能有人会注意到,在一些情况下,比如 e , l , h e, l, h e,l,h中有某个数为1,那么布局转换的代价就会超过运算的代价。因此,在必要的时候我们需要提供多种方案,在情况不同时采用。
4. 计算图的优化
对于单个张量计算而言,“上高速”——“跑高速”——“下高速”是一个完整链路,“上高速”、“下高速”相对于“跑高速”而言,时间一般比较少,也没有太多优化空间。而在深度学习模型的推理过程中,由于多个张量计算先后执行,就产生了与普通程序相似的冗余计算,在“不关注中间结果”的前提下,可以进行优化以进一步提升。
A = Input();
B = Const();
C = MatMul(A, B);
D = Const();
E = MatMul(C, D);
比如上面代码,矩阵乘之后接矩阵乘,且每个矩阵乘的输入之一是常量。展开之后类似这样:
A = Input();
B = Const();
AT = Convert(A);
BT = Convert(B)
CT = Strassen_MatMul(AT, BT);
C = Revert(CT);
CT = Convert(C);
D = Const();
DT = Convert(D);
ET = Strassen_MatMul(CT, DT);
E = Revert(ET);
很自然地我们会发现如下的冗余计算:
1、B、D 是常量,BT、DT 可以预先计算
2、CT -> C 和 C->CT 两步可以去掉
推理引擎除了提供一系列高效张量计算实现之外,冗余计算的清除也是非常重要的,主要的策略是:
1、“车同轨”:各类张量计算尽量按照相似的内存布局进行计算,减少切换成本。
2、“书同文”:将各类张量计算按一定的接口要求改造,便于调度模块根据这些接口进行冗余计算的清除。
具体到 MNN 中,表现为如下几个设计:
4.1 形实分离
MNN 要求所有算子实现的形状计算与内容计算分离,形状计算为各种硬件实现共用,内容计算由各类硬件抽象实现。
如 Pooling 算子的计算,被拆解为如下文件:
形状计算:
source/shape/ShapePool.cpp
各种硬件下的内容计算
source/backend/cpu/CPUPool.hpp // ARM / x86 等实现
source/backend/opencl/execution/PoolExecution.hpp // 基于 OpenCL 标准的实现
source/backend/vulkan/execution/VulkanPool.hpp // 基于 Vulkan 标准实现
source/backend/opengl/GLPool.cpp // 基于 OpenGL ES 3.1 的实现
这样做的好处是:
(1)减少异构计算支持的成本
(2)便于统一内存分配管理
(3)便于统一计算调度
4.2 NC4HW4布局
基于ARM / GPU 上的4单元SIMD,及大部分图像相关的算子可天然在通道并行的特性,MNN 对大部分CV相关算子采用NC4HW4 布局计算,这个布局设计可以在多数情况下减少内存布局转化的开销。

4.3 Resize机制 / 预推理机制
为了避免在推理中频繁申请和释放内存,减少异构计算中的冗余,MNN设计时引入一个预推理过程(接口上为 resize)。
这样做,可以在支持动态形状(即输入的形状可变的情况,允许运行时改变输入形状大小)的前提下达到如下目的:
(1)计算策略调度:根据输入形状决定一些算子的最优计算策略。
(2)进行内存管理:申请每个算子的输入输出Tensor内存与运算时所需的缓存,并按依赖关系复用中间算子的内存,这样既在运算过程中无内存申请/释放的损耗,也不会过多占用系统内存。
(3)冗余计算清除:在形状确定的情况下,部分算子的输出是固定的,如Priorbox,这些可以预先计算。另外对异构设备来说,如 Vulkan ,可以制作相关算子的命令缓冲(Command Buffer),填充参数等等,在执行过程中仅需提交 Command Buffer,将CPU-GPU的交互降到最低。
4.4 Fuse (算子融合)
在模型转换阶段,也即离线将一些算子合并或消除,如 scale 与 convolution 合并,relu 与 convolution 合并,这部分依赖于对具体算子的分析制定专家规则。
对于常用算子而言,MNN 在冗余计算的清除上已经做得比较好,但对于更复杂的算子处理上,仍有较多优化空间。业界也有基于编译技术进行冗余计算清除的,比如XLA(Tensorflow),TVM,但目前主要局限于Fuse,且还是靠专业经验去堆,不见得有更简单的做法。此外除了冗余计算清除外,业界也有不少研究异构调度,将计算拆解后分配到不同硬件上,由于未有成熟方案,不多叙述。
5. 展望
关于张量计算领域的未来发展,目前主要关注点还在于深度学习推理引擎的优化,像软硬协同、编译优化、模型压缩被经常提及。这里我想谈一些不同的视角:
(1)近些年来高性能计算的硬件层出不穷,华为、高通、苹果、谷歌、MTK都有自研的NPU,大家都支持一些核心的Op,但支持粒度参差不齐,也没几家愿意开放指令集。这种碎片化的现状目前来看会长期存在,承认碎片化的现状,梳理各类张量计算的逻辑,使它们能基于几个相对固定的被硬件所支持的高性能计算模块去实现,对接各个厂商去实现这少量模块,相对于统一标准、基于编译技术实现跨硬件,目前来看是更现实更可行的做法。
(2)由于历史原因,在图像与机器学习领域,张量被定义为多维数组,而这种定义在处理形变时显得繁琐,我们需要大量的算子去支持缩放、平移、裁剪功能,是否有更好的定义与计算方式,值得进一步探讨。
(3)除了深度学习以外,还有更多应用张量计算的场景,如图形图像、科学计算等,但这些领域往往是使用单独的张量计算库,少见像深度学习框架那样的清除冗余的机制,也没有求导的能力。未来深度学习框架与这些领域打通,可以赋予它们学习能力,也可以进一步优化性能,统一调度硬件。Tensorflow 已经推出了 Tensorflow Graphics 以做尝试,但后效如何还需观察。
参考链接:
http://www.jos.org.cn/html/2018/8/5563.htm
https://halide-lang.org/docs/index.html
https://github.com/alibaba/MNN
