决策树算法梳理（从原理到示例）

决策树是最经典的机器学习模型之一。它的预测结果容易理解，易于向业务部门解释，预测速度快，可以处理类别型数据和连续型数据。本文的主要内容如下：

• 信息熵及信息增益的概念，以及决策树的节点分裂的原则；
• 决策树的创建及剪枝算法；
• scikit-learn中决策树算法的相关参数；
• 使用决策树预测泰坦尼克号幸存者示例；
• scikit-learn中模型参数选择的工具及使用方法；
• 聚合（融合）算法及随机森林算法的原理。

注意：本文内容篇幅超长，请各位客官根据需要选择性“品尝”。
开始正文

1 算法原理

决策树是一个类似于流程图的树结构，分支节点表示对一个特征进行测试，根据测试结果进行分类，树叶节点代表一个类别。这里面最核心的问题是，在创建决策树的过程中，要先对哪个特征进行分裂？要回答这个问题，我们需要从信息的量化谈起。

1.1 信息增益

我们天天谈论信息，那么信息要怎么样来量化呢？1948年，香农在《通信的数学原理》中提出了信息熵（Entropy）的概念，从而解决了信息的量化问题。香农认为，一条信息的信息量和它的不确定性有直接关系。一个问题的不确定性越大，要搞清楚这个问题，需要了解的信息就越多，其信息熵就越大。信息熵的计算公式为：
$H(X)=-{\sum }_{x\in X}P(x)lo{g}_{2}P(x)$，其中$P(x)$表示事件x出现的概率。
例如，一个盒子里分别有5个白球和5个红球，随机取出一个球。问：这个球是白的还是红的？这个问题的信息量有多大？由于红球和白球出现的概率都是1/2，代入信息熵公式，可以得到其信息熵为：
$H(X)=-(\frac{1}{2}lo{g}_2\frac{1}{2}+\frac{1}{2}lo{g}_2\frac{1}{2})=1$
即这个问题的信息量是1 bit。对，信息量的单位是比特！我们要确定这个球是红的还是白的，只需要1 比特的信息就够了。对于极端的例子，对于确定的事件，其概率为1，其信息熵为0，因为我们不需要再获取任何新的信息就能知道结果。
回到决策树的构建问题上来，当我们要构建一棵决策树时，应该优先选择哪个特征来划分数据集（分裂节点）呢？答案是：遍历所有的特征，分别计算，使用这个特征划分数据集前后信息熵的变化值，然后选择信息熵变化幅度最大的那个特征，来优先作为划分数据集（分裂节点）的依据。即选择信息增益最大的特征作为分裂节点。

那么，信息增益的物理意义是什么呢？
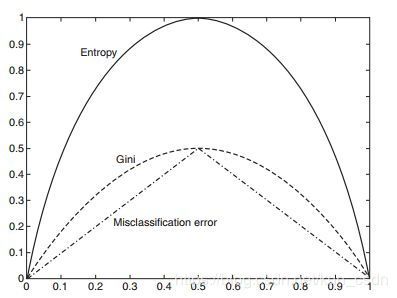
如果以概率P(x)为横坐标，以信息熵（Entropy）为纵坐标，把信息熵和概率的函数关系$Entropy=-P(x)lo{g}_{2}P(x)$在二维坐标系上画出来就可以看出(标有“Entropy”的曲线)，当概率P(x)越接近0或越接近1时，信息熵的值越小，其不确定性越小，即数据越“纯”。比如说当概率为1时，数据是最“纯净的”，已经消除了不确定性，其信息熵为0。我们在选择特征的时候，选择信息增益最大的特征，在物理意义上就是让数据尽量往更纯净的方向上变换。因此，信息增益是用来衡量数据变得更有序、更纯净的程度的指标。

熵是热力学中表征物质状态的参量之一，其物理意义是体系混乱程度的度量，被香农借用过来作为数据的混乱程度和信息量的度量。著名的熵增原理是这样描述的：孤立热力学系统的熵不减少，总是增大或者不变。

一个孤立系统不可能朝低熵的状态发展，即不会变得有序。用大白话讲就是，如果没有外力的作用，这个世界将是越来越无序的。人活着，在于尽量让熵变低，即让世界变得更有序，降低不确定性。当我们消费资源时，是一个增熵的过程。我们把有序的食物变成了无序的垃圾。例如，我们在写博客或者读博客的过程可以理解为减熵过程。我们通过写作和阅读，减少了不确定的信息，从而实现了减熵的过程。人生价值的实现在于消费资源（增熵过程）来获取能量，经过自己的劳动付出（减熵过程）让世界变得更加纯净有序。信息增益（减熵量-增熵量）就是衡量人生价值的尺度。

1.2 决策树的创建

决策树的构建过程，就是从训练数据集中归纳出一组分类规则，使它与训练数据矛盾较小的同时具有较强的泛化能力。有了信息增益来量化地选择数据集的划分特征，使决策树的创建过程变得更加容易了，决策树的创建基本上分为：

• 计算数据集划分前的信息熵。
• 遍历所有未作为划分条件的特征，分别计算根据每个特征划分数据集后的信息熵。
• 选择信息增益最大的特征，并使用这个特征作为数据划分节点来划分数据。
• 递归地处理被划分后的所有子数据集，从未被选择的特征里继续选择最优数据划分特征来划分子数据集。

问题来了，递归过程什么时候结束呢？一般来讲，有两个终止条件，一是所有的特征都用完了，即没有新的特征可以用来进一步划分数据集。二是划分后的信息增益足够小了，这个时候就可以停止递归划分了。针对这个停止条件，需要事先选择信息增益的阈值来作为结束递归的条件。
使用信息增益作为特征选择指标的决策树构建算法，称为ID3算法。以后还会延伸到C4.5、CART等算法。

1.2.1 离散化

细心的人可能会发现一个问题：如果一个特征是连续值怎么办呢？比如说年龄，这个时候怎么用决策树来建模呢？答案是：离散化。通俗地说就是分区间、分桶，比如10岁到25岁的年龄段标识为类别A，26岁到35岁的年龄段标识为类别B等等。经过离散处理后，就可以用来构建决策树了。要离散化成几个类别，这个往往和具体的业务相关。

1.2.2 正则项

最大化信息增益来选择特征，在决策树的构建过程中，容易造成优先选择类别最多的特征进行分类。举一个极端的例子，我们把某个产品的唯一标识符ID作为特征之一加入到数据集中，那么构建决策树时，就会优先选择产品ID来作为划分特征，因为这样划分出来的数据，每个叶子节点只有一个样本，划分后的子数据集最“纯净”，其信息增益最大。但是这并不是我们希望看到的结果。
解决办法是，计算划分后的子数据集的信息熵时，加上一个与类别个数成正比的正则项，来作为最后的信息熵。这样，当算法选择的某个类别较多的特征时，由于受到类别个数的正则项惩罚，导致最终的信息熵也比较大。这样通过合适的参数，可以使算法训练得到某种程度的平衡。
另外一种解决办法是使用信息增益比来作为特征选择的标准。这就是C4.5算法构建标准。

1.2.3 基尼不纯度

既然信息熵是衡量信息不确定性的指标，实际上也是衡量信息“纯度”的指标。除信息熵外，基尼不纯度（Gini impurity）也是衡量信息不纯度的指标，其计算公式如下：
$Gini(D)={\sum }_{x\in X}P(x)(1-P(x))=1-{\sum }_{x\in X}P(x{)}^2$
其中，$P(x)$是样本属于x这个类别的概率。如果所有的样本都属于一个类别，此时$P(x)=1$，则$Gini(D)=0$，即数据不纯度最低，纯度最高。看下面的图示（标有“Gini”字样的曲线）。

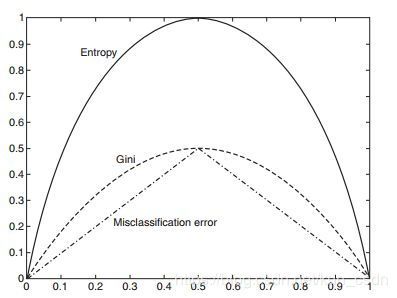
从图形可以看出，其形状和信息熵的形状几乎一样。CART算法使用基尼不纯度作为特征选择标准。CART也是一种决策树的构建算法。

1.3 剪枝算法

使用决策树模型拟合数据时，容易造成过拟合。解决过拟合的方法是对决策树进行剪枝处理。决策树的剪枝有两种思路：前剪枝（Pre-Pruning）和后剪枝（Post-Pruning）。

1.3.1 前剪枝

前剪枝是在构造决策树的同时进行剪枝。在决策树的构建过程中，如果无法进一步降低信息熵的话就会停止创建分支。为了避免过拟合，可以设定一个阈值，信息熵减小的数量小于这个阈值，即使还可以继续降低信息熵，也停止继续创建分支。这种方法称为前剪枝。比如限制叶子节点的样本个数，当样本个数小于一定的阈值时，不再继续创建分支。

1.3.2 后剪枝

后剪枝是指决策树构建完成后进行剪枝。剪枝的过程是对拥有同样父节点的一组节点进行检查，判断如果将其合并，信息熵的增加量是否小于某一阈值。如果小于阈值，则这一组节点可以合并为一个节点。后剪枝的过程是删除一些子树，然后用子树的根节点替代，来作为新的叶子节点。这个新叶子节点所标识的类别通过大多数原则来确定，即把这个叶子节点里样本最多的类别作为这个叶子节点的类别。

2 算法参数

scikit-learn使用sklearn.tree.DecisionTreeClassifier类来实现决策树分类算法。其中几个典型的参数解释如下：

• criterion：特征选择算法。一种基于信息熵，另一种基于基尼不纯度。有人说两种算法的差异性不大，对模型准确性没有太大影响。
• splitter：创建决策树分支的选项，一种是选择最优的分支创建原则，另外一种是从排名靠前的特征中，随机选择一个特征来创建分支，这个方法和正则项的效果类似，可以避免过拟合。
• max_depth：指定决策树的最大深度，可以避免过拟合。
• min_samples_split：指定能创建分支的数据集的大小，默认是2。这是一种前剪枝的方法。
• min_samples_leaf：创建分支后的节点样本数量必须大于等于这个数值，否则不再创建分支。这是一种前剪枝的方法。
• max_leaf_nodes：除了限制最小的样本节点个数（和参数min_samples_leaf有关），该参数可以限制最大的样本节点个数。
• min_impurity_split：可以使用该参数来指定信息增益的阈值。决策树在创建分支时，信息增益必须大于这个阈值，否则不创建分支。

从这些参数可以看到，scikit-learn有一系列的参数用来控制决策树生成的过程，从而解决过拟合问题。

3 实例：预测泰坦尼克号幸存者

数据集下载链接：https://pan.baidu.com/s/1p-OdLtRF6e_vxlX8hF5OHw
提取码：778z
数据集中总共有两个文件，都是csv格式的数据。其中，train.csv是训练数据集，包含已标注的训练样本数据；test.csv是我们的模型要进行幸存者预测的数据。我们的任务就是根据train.csv里的数据训练出模型，用这个模型去预测test.csv里的数据。

3.1 数据分析

train.csv是一个892行、12列的数据表格，意味着我们有891个训练样本（表头除外），每个样本有12个特征，我们需要先分析这些特征，以便决定哪个特征可以用来进行模型训练。

• PassengerId：乘客的ID号，这个是顺序编号，用来唯一地标识一名乘客。这个特征和幸存与否无关，我们不使用这个特征。
• Survived：1表示幸存，0表示遇难。这个是我们的标注数据。
• Pclass：仓位等级，是很重要的特征。看过电影的同学都知道（没看过的童鞋赶快去补上），高仓位等级的乘客能更快地达到甲板，从而更容易获救。
• Name：乘客名字，这个特征和幸存与否无关，我们会丢弃这个特征。
• Sex：乘客性别，回想一下电影的情节就知道，由于救生艇数量不够，船长让妇女和儿童先上救生艇。所以这是一个很重要的特征。
• Age：乘客年龄，儿童会优先登上救生艇，身强力壮者的幸存概率也会更高一些。
• SibSp：兄弟姐妹同在船上的数量。
• Parch：同船的父辈人员数量。
• Ticket：乘客票号。我们不使用这个特征。
• Fare：乘客的体热指标。
• Cabin：乘客所在的船舱号。实际上这个特征和幸存与否有一定的关系，比如最早被水淹没的船舱位置，其乘客的幸存概率要低一些。但由于这个特征有大量的缺失值，而且没有更多的数据来对船舱进行归类，因此我们丢弃这个特征的数据。
• Embarked：乘客登船的港口。我们需要把港口数据转换为数值型数据。

我们需要加载csv文件，并做一些预处理，包括：

• 提取Survived列的数据作为模型的标注数据。
• 丢弃不需要的特征数据。
• 对数据进行转换，以便模型处理。比如性别数据，我们需要转换为0和1.
• 处理缺失数据。比如年龄这个特征，有很多缺失值。

我们使用pandas进行处理操作：

import pandas as pd 
import numpy as np

# 读取数据，指定第一列作为行索引
data = pd.read_csv('train.csv', index_col=0) # PassengerId作为行索引

#查看一下前5行数据
data.head()

输出如下（本人使用的是jupyter notebook）：

data.info() # 查看数据集的基本信息

输出如下：

根据上面的信息可以看到，train.csv中有891个训练样本，索引从1到891；每一列的数据类型；一共有11列；Age列、Cabin列和Embarked列都有缺失值。
接下来要按照我们前面讲到的内容对数据进行处理。

# 丢弃无用的数据
data.drop(['Name', 'Ticket', 'Cabin'], axis=1, inplace=True)

# 处理性别数据。女性为1，男性为0
data['Sex'] = (data['Sex'] == 'male').astype('int')

# 处理登船港口数据
labels = data['Embarked'].unique().tolist()
data['Embarked'] = data['Embarked'].apply(lambda n: labels.index(n))

# 处理缺失值
data = data.fillna(0)

data.head()

输出如下：

大家可以将之前的输出和这时候的输出进行对比，会发现一些不同。

3.2 模型训练

首先，我们需要把Survived列提取出来作为标签，然后在原数据集中将其丢弃。同时把数据集分成训练集和交叉验证数据集。

from sklearn.model_selection import train_test_split

y = data["Survived"].values
X = data.drop(["Survived"], axis=1).values

# 幸亏这个数据集不大，我们可以对每一步的操作结果输出查看。限于篇幅，这里请读者自行操作
print(y)
print(X)

X_trian, X_test, y_trian, y_test = train_test_split(X, y, test_size=0.2)
print("train dataset: {0}; test dataset: {1}".format(X_trian.shape, X_test.shape))
# 输出：train dataset: (712, 7); test dataset: (179, 7)

# 使用scikit-learn的决策树模型对数据进行拟合。
from sklearn.tree import DecisionTreeClassifier

clf = DecisionTreeClassifier()
clf.fit(X_trian, y_trian)
train_score = clf.score(X_trian, y_trian)
test_score = clf.score(X_test, y_test)
print('train score: {0}; test score: {1}'.format(train_score, test_score))
# 输出：train score: 0.9831460674157303; test score: 0.7932960893854749

从输出数据可以看出，针对训练样本评分很高，但针对交叉验证数据集的评分比较低，两者差距较大。很明显，这是过拟合的特征。解决决策树过拟合的方法是剪枝。不幸的是，scikit-learn不支持后剪枝，但提供一系列的模型参数进行前剪枝，例如，我们可以通过$max\_depth$参数限定决策树的深度，当决策树达到限定深度时就不再进行分裂了。这样就可以在一定程度上避免过拟合。

3.3 优化模型参数

问题来了，难道要手动一个一个地去试参数，然后找出最优的参数吗？程序员都是信奉DRY（Do not Repeat Yourself）原则的群体，一个最直观的解决办法是选择一系列参数的值，然后分别计算用指定参数训练出来的模型的评分数据。
以模型深度$max\_depth$为例，我们先创建一个函数，它使用不同的模型深度训练模型，并计算评分数据。

# 参数选择
def cv_score(depth):
    clf = DecisionTreeClassifier(max_depth = depth)
    clf.fit(X_trian, y_trian)
    tr_score = clf.score(X_trian, y_trian)
    cv_score = clf.score(X_test, y_test)
    return (tr_score, cv_score)

# 接着构造参数范围，在这个范围内分别计算模型评分，并找出评分最高的模型所对应的参数。
depths = range(2, 15)
scores = [cv_score(d) for d in depths] # 在这里开始使用不同的树深训练模型，得到模型得分
tr_scores = [s[0] for s in scores]
cv_scores = [s[1] for s in scores]

# 找出交叉验证数据集评分最高的索引
best_score_index = np.argmax(cv_scores)
best_score = cv_scores[best_score_index]
best_param = depths[best_score_index]  # 找出对应参数
print("best param: {0}; best score: {1}".format(best_param, best_score))

# 输出：best param: 5; best score: 0.8324022346368715

可以看到，针对模型深度这个参数，最优的值是7，其对应的交叉验证数据集评分为0.8324.我们还可以把模型参数和模型评分画出来，更直观地观察其变化规律。

import matplotlib.pyplot as plt
plt.figure(figsize=(6,4), dpi=144)
plt.grid()
plt.xlabel("max depth of decision tree")
plt.ylabel("score")
plt.plot(depths, cv_scores, '.g-', label='cross-validation score')
plt.plot(depths, tr_scores, '.r--', label='training score')
plt.legend()
plt.savefig('depths_scores.png')

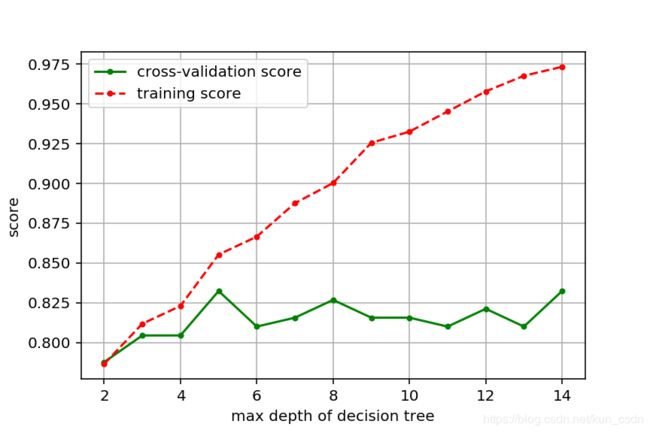
使用同样的方法，我们可以观察参数$min\_impurity\_split$。这个参数用来指定信息熵或者基尼不纯度地阈值，当决策树分裂后，其信息增益低于这个阈值，则不再分裂。

def cv_score2(val):
    clf = DecisionTreeClassifier(criterion='gini', min_impurity_split=val)
    clf.fit(X_trian, y_trian)
    tr_score = clf.score(X_trian, y_trian)
    cv_score = clf.score(X_test, y_test)
    return (tr_score, cv_score)

# 指定参数范围，分别训练模型并计算模型评分
values = np.linspace(0, 0.5, 50)  # 0到0.5之间50等分
scores = [cv_score2(v) for v in values] # 在这里开始使用不同的树深训练模型，得到模型得分
tr_scores = [s[0] for s in scores]
cv_scores = [s[1] for s in scores]

# 找出交叉验证数据集评分最高的索引
best_score_index = np.argmax(cv_scores)
best_score = cv_scores[best_score_index]
best_param = values[best_score_index]  # 找出对应参数
print("best param: {0}; best score: {1}".format(best_param, best_score))

# 画出模型参数与模型评分的关系
plt.figure(figsize=(6,4), dpi=144)
plt.grid()
plt.xlabel("threshold of entropy")
plt.ylabel("score")
plt.plot(values, cv_scores, '.g-', label='cross-validation score')
plt.plot(values, tr_scores, '.r--', label='training score')
plt.legend()
plt.savefig('entropy_scores.png')

# 输出：best param: 0.18367346938775508; best score: 0.8603351955307262

我们把[0, 0.5]之间50等分，以每个等分点作为信息增益阈值来训练一次模型，并计算评分数据。从图中可以看出，阈值接近0.5时，模型的训练评分和交叉验证评分都急剧下降，说明模型出现了欠拟合。

思考一下，如果把决策树特征选择的标准由基尼不纯度改为信息熵，即把参数$criterion{=}^{\prime }gin{i}^{\prime }$改为$criterion{=}^{\prime }entrop{y}^{\prime }$后，图形有什么变化？为什么？修改完后，是否需要重新调整代码中变量$values$的范围？

3.4 模型参数选择工具包

前面我们讲的模型参数优化方法有两个问题。
一是数据不稳定，每次重新把数据集划分成训练集和交叉验证集后，选择出来的模型参数就不是最优的了。因为数据是随机划分出来的。
例如，原来选择出来的决策树深度的最优值为7，第二次计算出来的决策树最优深度可能就变成了8。
二是，不能一次选择多个参数。例如，我们想要尝试找出$max\_depth$和$min\_samples\_leaf$两个结合起来的最优参数就没办法实现。

人总是能找到解决麻烦问题的办法。scikit-learn在$sklearn.model\_selection$包里提供了大量的，模型选择和评估的工具供我们使用。
对于上面的两个问题，我们使用$GridSearchCV$类来解决。下面看一下例子：

from sklearn.model_selection import GridSearchCV

thresholds = np.linspace(0, 0.5, 50)
# 设置参数矩阵
param_grid = {
    'min_impurity_split': thresholds
}

clf = GridSearchCV(DecisionTreeClassifier(), param_grid=param_grid, cv=5)
clf.fit(X, y)
print("best param: {0}; \nbest score: {1}".format(clf.best_params_, clf.best_score_))

# 输出：
# best param: {'min_impurity_split': 0.21428571428571427}; 
# best score: 0.8226711560044894

其中关键的参数是$param\_grid$，它是一个字典，字典关键字对应的值是一个列表，$GridSearchCV$会枚举列表里的所有值来构建模型，多次计算训练模型及评分，最终得出指定参数值的平均评分和标准差。
另外一个关键的参数是cv，它用来指定交叉验证集的生成规则，cv=5表示每次计算都把数据集分成5份，拿其中一份作为交叉验证集，其他的作为训练集。最终得出的最优参数和最优评分保存在$clf.best\_params\_$和$clf.best\_score\_$里。
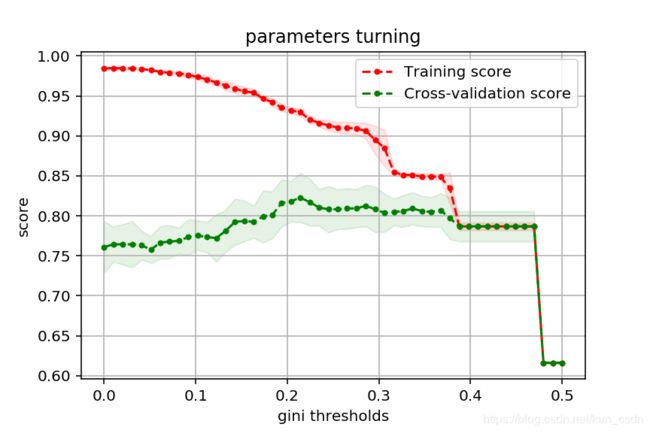
此外，$clf.\_results\_$保存了计算过程的所有中间结果。我们可以拿这个数据来画出模型参数与模型评分的关系图：

def plot_curve(train_sizes, cv_results, xlabel):
    train_scores_mean = cv_results["mean_train_score"]
    train_scores_std = cv_results["std_train_score"]
    
    test_scores_mean = cv_results["mean_test_score"]
    test_score_std = cv_results["std_test_score"]
    
    plt.figure(figsize=(6, 4), dpi=144)
    plt.title('parameters turning')
    plt.grid()
    plt.xlabel(xlabel)
    plt.ylabel('score')
    plt.fill_between(train_sizes,
                    train_scores_mean - train_scores_std,
                    train_scores_mean + train_scores_std,
                    alpha=0.1, color='r')
    plt.fill_between(train_sizes,
                    test_scores_mean - test_score_std,
                    test_scores_mean + test_score_std,
                    alpha=0.1, color='g')
    plt.plot(train_sizes, train_scores_mean, '.--', color='r', label='Training score')
    plt.plot(train_sizes, test_scores_mean, '.--', color='g', label='Cross-validation score')
    
    plt.legend(loc='best')
    plt.savefig('parameters turning.png')

我们来看一下如何在多组参数之间选择最优的参数组合：

from sklearn.model_selection import GridSearchCV
entropy_thresholds = np.linspace(0,1,50)
gini_thrsholds = np.linspace(0,0.5,50)

# 设置参数矩阵
param_grid = [
    {
        'criterion':['entropy'],
        'min_impurity_split': entropy_thresholds
    },{
        'criterion':['gini'],
        'min_impurity_split': gini_thrsholds
    },{
        'max_depth':range(2,10)
    },{
        'min_samples_split': range(2,30,2)
    }
]

clf = GridSearchCV(DecisionTreeClassifier(), param_grid, cv=5)
clf.fit(X, y)
print("best param: {0}; \nbest score: {1}".format(clf.best_params_, clf.best_score_))

# 输出：
# best param: {'criterion': 'entropy', 'min_impurity_split': 0.5306122448979591}; 
# best score: 0.8249158249158249

代码的关键部分还是$param\_grid$参数，它是一个列表，列表的每个元素都是一个字典，每个字典都是一套参数。

4 集合算法

聚合算法（Ensemble）是一种元算法（Meta-algorithm），它利用统计学采样原理，训练出成百上千个不同的算法模型。当需要预测一个新样本时，使用这些模型分别对这个样本进行预测，然后采用少数服从多数的原则，决定新样本的类别。集合算法可以有效地解决过拟合问题。在scikit-learn里，所有地集合算法都实现在$sklearn.ensemble$包里。

4.1 自助聚合算法 Bagging

$Bagging$是Bootstrap Aggregating的缩写。它的核心思想是，采用有放回的采样规则，从$m$个样本的原数据集里进行$n（n\le m）$次采样，构成一个包含$n$个样本的新训练集，然后拿这个新训练集训练模型。重复上述过程$B$次，得到$B$个模型。当有新样本需要进行预测时，拿那$B$个模型分别对这个样本进行预测，然后采用投票方式（分类问题）或求平均值（回归问题）得到新样本的预测值。
由此可见，随机采样出来的数据集里可能有重复数据，并且在原数据集里，不一定每个数据都会出现在新采样出来数据集里。单一模型往往容易对噪声数据敏感，造成高方差$(HighVariance)$。$Bagging$可以降低对噪声数据的敏感性，从而提高模型准确性和稳定性。这种方法不需要额外的输入，只是简单地对同一个数据集训练出多个模型即可实现。当然，代价是会增加模型训练的计算量。
在scikit-learn中，由$BaggingClassifier$和$BaggingRegressor$分别实现分类和回归的$Bagging$算法。

4.2 正向激励算法 boosting

算法原理是，初始化时，针对有m个训练样本的数据集，给每个样本都分配一个初始权重，然后使用这个带权重的数据集来训练模型。训练出这个模型后，针对这个模型预测错误的样本，增加其权重值，然后拿这个新的带权重的数据集来训练出一个新模型。重复上述过程B次，训练出B个模型。它与Bagging算法的区别如下：

• 采样规则不同。Bagging算法是有放回的随机采样规则，而boosting是使用增大错误预测样本的权重的方法，这一方法相当于加强对错误预测的样本的学习力度，从而提高模型准确性。
• 训练方式不同。Bagging算法可以并行训练多个模型，而boosting算法只能串行训练，因为下一个模型依赖于上一个模型的预测结果。
• 模型权重不同。Bagging算法训练出来的B个模型权重是一样的，而boosting算法训练出来的模型本身带着权重信息，在对新样本进行预测时，每个模型的权重是不一样的。单个模型的权重由模型训练的效果来决定，即准确性高的模型权重更高。

boosting算法实现有很多种，其中最著名的是$AdaBoost$算法。在scikit-learn里由$AdaBoostClassifier$和$AdaBoostRegressor$分别实现分类和回归算法。

4.3 随机森林

随机森林在自助聚合算法（Bagging）的基础上更进一步，对特征应用自助聚合算法。也就是说，每次训练时，不拿所有的特征来训练，而是随机选择一个特征的子集来进行训练。随机森林算法有两个关键参数，一是构建的决策树的个数$t$，二是构建单棵决策树特征的个数$f$。
假设针对一个有$m$个样本、$n$个特征的数据集，则其算法原理如下：

4.3.1 单棵决策树的构建

• 采用有放回采样，从原数据集中经过$m$次采样，获取到一个有$m$个样本的数据集（可能有重复的样本）。
• 从$n$个特征里，采用无放回采样规则，从中取出$f$个特征作为输入特征。
• 在新数据集上，（有m个样本，f个特征的数据集上），构建决策树。
• 重复上述过程$t$次，构建出$t$棵决策树。

4.3.2 随机森林的分类结果

生成$t$棵决策树之后，对于每一个新的测试样本，综合多棵决策树的预测结果来作为随机森林的预测结果。具体为：

• 若目标为数字类型，取$t$棵决策树的预测值的平均值作为预测结果。【Averaging】
• 若目标为分类问题，采取少数服从多数，取单棵树分类结果最多的那个类别作为整个随机森林的分类结果。

为什么随机森林要选取特征的子集来构建决策树？

假如某个输入特征对预测结果是强关联的，那么如果选择全部特征来构建决策树时，这个特征会在所有的决策树里体现。 由于这个特征和预测结果强关联，造成所有的决策树都强烈地反映这个特征的“倾向性”，从而导致无法很好地解决过拟合问题。
其实在线性回归算法中，通过增加正则项来解决过拟合问题，原理就是确保每个特征都对预测结果有少量的贡献，避免单个特征对预测结果有过大贡献而导致过拟合。这里的原理是一样的。

在scikit-learn里，由$RandomForestClassifier$和$RandomForestRegressor$分别实现随机森林的分类和回归算法。

==========================================================================