成为数据科学家,需具备这些技能
目前数据科学和数据科学家成为了流行词汇。当有人问你干什么,你回答说数据科学家,对方会恍然大悟,觉得特别高大上,噢,数据科学家啊,听说过。是啊,没听说过数据科学家那就out了。如果接着问,数据科学家具体干什么的?然后就没有然后了。
不知道你们有没有听说过这样一则轶事,美国最高法院法官Potter Stewart被问到什么是淫秽时,他回答:“看下才知道。”这和数据科学很类似,很多概念,在大而化之的时候都可以存在,大家口耳相传,聊的不亦乐乎,但一追究细节,立即土崩瓦解。那么什么是数据科学家呢?我从谷歌查询了数据科学家的定义,下面是其中的一些:
-
住在加州的数据分析师;
-
数据科学家是商业(数据)分析师的进化版;
-
比软件学家更懂统计,比统计学家更懂软件科学的人;
-
拥有出众数据分析能力的BI咨询师,尤其是能用大量数据增加商业竞争力的人;
-
会编程,懂统计,能通过多种方式从数据中掘金的人。
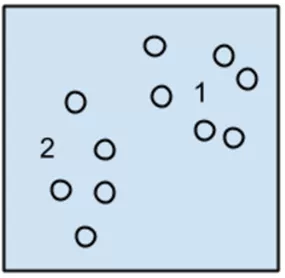
此外,很多其他职位其职责都和“从数据中获取信息”有关,比如:数据分析师,BI咨询师,统计学家,金融分析师,商业分析师,预测分析师……这些不同职业有什么区别?即便都是数据科学家,教育背景等也是千差万别的。由于媒体的炒作以及对“数据科学家”这个名称的滥用,尽管总的分析行业正在飞速发展,但大家对这个行业从业人员的认识却越来越混乱。现在大部分商业领域所谓的分析都达不到“科学”的程度,而仅仅是加减乘除的游戏,数据科学工作职位比较如图1-1所示。
图1-1
这些不同的职位要求有何不同?在北美总体说来:
-
金融分析师一般有金融方向的MBA学位。他会用电子表格,知道会计软件,分析各部门的预算数据,分析实际经营结果和预测之间的差别,做一些预测,但这里的预测不会涉及复杂的机器学习和统计模型。
-
数据分析师一般有MBA学位,有一些计算机背景,很擅长使用电子表格,会用高阶的电子表格编程功能如VBA、自定义函数、宏。根据情况,会使用一些BI的软件,如Tableau,主要都是用鼠标点拖的方式。会用SQL从数据库中读取数据。我所见的商业分析师拥有很少(或没有)统计知识。所以这部分人有处理数据的知识,但是没有统计学的知识,能做的分析非常有限。
-
统计学家一般多在药厂、生物技术公司,做一些非常传统的混合效应模型、方差分析等生物统计分析。由于行业要求,多用SAS而非开源软件R。
-
BI咨询师,一般也是工商管理专业,有MBA学位,受传统的商学院教育(熟悉4Ps或6Ps,4Cs,使用SWOT法分析市场),熟练使用电子表格,很少或没有其他技术背景。
-
数据科学家,多是数学/统计、计算机、工程学专业出身,会使用R, Python等多种编程语言,熟悉数据可视化。大多数在入职前没有太多市场营销知识。掌握高等概率统计,熟悉如下概念:抽样,概率分布,假设检验,方差分析,拟合优度检验,回归,时间序列预测模型,非参数估计,实验设计,决策树,马尔可夫链,贝叶斯统计(很快就能在白板上写下贝叶斯定理)。
数据科学家都分布在哪些行业呢?根据Burtch Works Executive Recruiting在2015年4月发布的“数据科学家薪资调查报告”,科技(包括互联网)公司是数据科学家最大的雇主。其次是一些为其他公司提供如广告、市场调查、市场分析等商业服务的公司。这两者之和超过了50%。2014年创业公司雇佣了29.4%的数据科学家,2015年这个比例降至14.3%,原因不是创业公司招的数据科学家职位少了,而是大公司招入的数据科学家增长迅速,整体基数变大。
总体来说,数据科学家就业前景在北美是非常好的。调查还显示,在北美,大部分(70%)数据科学家工作经验还不到10年,因此数据科学还是个很年轻的行业。现在,大家对数据科学领域应该有个大致的感觉了。下面我们对其进一步探讨。
什么是数据科学
50年前,John Tukey他老人家就预言有个类似今天的数据科学的东西会出现。早在1962年,他在“数据分析的未来(The Future of Data Analysis)”中就嚷着要对学术统计进行改革。这篇文章当时发表在“数理统计年鉴(The Annals of Mathematical Statistics)”上,他的观点震惊了许多统计界的同事,这都是一群根正苗红的数理统计出身的大神们,那时数理统计年鉴中的文章都是满满的数学公式推导,从定义、定理到证明,逻辑缜密,理论精确。当然牛人最大的特点就是可以随时任性。John推导了大半辈子公式,突然有一天发现统计不是这么玩的,于是他跳出来说:
“很长一段时间我觉得自己是统计学家,对统计推断情有独钟,将从小样本上研究得到的结论推广到更大的群体。但随着数理统计的发展,我越发觉得这个路数不大对……总的来说,我觉得自己感兴趣的是数据分析,它包括:分析数据的过程,解释该过程得到结果的技术,合理计划收集数据的方案,使得之后的分析过程更方便准确,以及所有的分析中需要用到的仪器和数学理论。”
用简短的一句话概括就是:仅仅研究数学理论不是数据科学,数据科学的内容涵盖更广。
美国密歇根大学在2015年9月宣布了一个1亿美金的“数据科学项目(Data Science Initiative)”,计划在未来4年聘请35名新教授,支持与数据相关的跨学科研究。大学媒体大胆地宣称:
“数据科学已经成为第4大科学发现手段,前3个为:实验、模型和计算。”
这里的数据科学指的是什么?该项目的网站上有如下对数据科学的描述:
“数据科学是科学发现和实践的结合,其包括对大量类型各异的数据进行收集、管理、清理、分析、可视化和结果解释。其应用遍及各种科学、平移和交叉领域。”
如前所述,数据科学是一个新兴领域。在美国,对数据分析类专业人才的需求不断上升。研究估计[2],从2015到2018年,美国预计有400~500万个工作岗位要求数据分析技能,大部分这些岗位的人才需要经过特殊训练。前面已经介绍过各种和数据分析相关的行业,这些行业对专业训练的要求参差不齐。其中数据科学家的门槛是最高的。成为一个数据科学家不是件容易的事。不可否认,即使是数据科学家这个职业名称,当前也被滥用了。这些工作的本质都是从数据中获取信息。
我是这样定义数据科学的:
数据科学=数据+科学=从数据中获取信息的科学
这是一门新的科学,有各种因素推动了这门科学的产生。John提到了如下的4个驱动因素:
-
正统统计学理论;
-
计算机和电子显示设备的高速发展;
-
很多领域内更多更大的数据提出的挑战;
-
定量分析在更广的领域受到重视。
很难想象这些观点是在1962年提出的,现在看来一点也不过时。当前这4个推动力都已经存在,这也是数据科学兴起的原因。
7年之后,Tukey和Wilk在1969年又将这门科学和已经存在的科学进行对比,进一步限定了统计学在数据科学中所扮演的角色:
“……数据科学是一个困难的领域。它需要和人们能用数据做什么和想用数据做什么这样的外在条件相适应。从某种意义上说,生物比物理困难,行为科学比这两者都难,很可能总体数据科学的问题比这三者还要难。无论在现在还是短期的将来,要建立一个正式的能够给数据分析实践提供高效指导的数据科学的结构还有很长的路要走。数据科学可以从正规正统统计学那里获得很多,但它们之间也需要保持适当的距离。”
数据科学不仅是个科学领域,而且和其他已经存在很久的科学领域一样困难。统计理论只在数据科学中扮演了部分角色。
但数据科学是纯科学吗?
什么样的东西能够称为科学?我们看看John Tukey在50年前是怎么说的[1]:
怎样才能称为科学呢?回答因人而异。但下面3点大多数人都同意:
-
智力内容(intellectual content);
-
用能让人理解的方式组织起来;
-
实践是检验其结果的最终标准。
第1条没有提供太多的信息,毕竟太多东西都有智力的内容,这个没有区分度。
第2条也没有办法将科学和艺术区别开来。
第3条我觉得才真正是区分科学和艺术的硬标准,也就是可证伪性。
数据科学符合前2条,但是不总是可以证伪的。对于预测消费者是否会再次购买这样的问题,可以用真实发生的行为来评估模型表现。以及很多交互校验(cross-validation)的过程也能够用来评估模型。但对于很多市场调查数据的分析,就难以严格地科学证伪,比如分析消费者的品牌认知。对于人类心理学和行为学的研究本身就是有艺术的成分,因此相关的数据科学也同时是一门艺术。但是这和瞎猜并不一样,或许可以这样描述:这是在当前信息下能得到的最好猜测。
计算机科学之父高德纳(Donald Knuth)在他1974年出版的图书《计算机程序设计的艺术》中如此定义科学:
“能够教给计算机的知识就是科学。”
从这个角度上看,数据科学的艺术部分就更高了。计算机是数据科学不可或缺的一部分,可以说是最重要的一部分,但绝对不是全部。我们能完全依赖计算机取代数据科学家吗?很难。因为计算机不能和客户交流,将一个现实的商业问题转化成数据问题。计算机本身并不能决定什么数据应该收集,什么不需要。计算机无法对数据的质量做出评估。计算机无法向人解释模型结果,更无法将模型结果转化成商业决策建议。
因此数据科学还有艺术的一面,艺术部分的发挥就需要数据科学家啦!
什么是数据科学家
数据科学家=数据+科学+艺术家=用数据和科学从事艺术创作的人
数据科学家立足于科学,但不止于科学。从数据中提取出信息无疑是重要且有意义的过程,但这还不够。因为分析的终极目标是能够解决问题,实现价值。而从信息到具体应用领域的知识,进而应用所得知识创造价值,这两步都是需要一些艺术的,需要一点想象力。在第3章“数据分析流程”中我会进一步讨论这个职业中艺术的部分。科学家需要不断学习,数据科学家是一个需要终身学习的职业,其实很多职业都要求这一点。当然,你进入这个领域之前有一个门槛得要跨过去,有些基本的技能需要掌握。上面关于数据科学以及数据科学家的定义听起来非常高大上,可能有些抽象,感觉自己是个文艺青年。其实也可以用一种更接地气的方式表达:
数据科学=从数据中得到问题答案的科学
数据科学家=通过科学方法从数据中得到有实际意义的问题答案的人
数据科学结合了一整套科学工具与技术(数学,计算,视觉,分析,统计,试验,问题界定,模型建立与检验等),用于从数据收集中获得新发现、洞察与价值。使用数据科学的根本目的是解决实际问题。David Donoho在他2015年的文章《数据科学50年(50 years of Data Science)》[3]中讨论了当今数据科学的全貌,其中他将数据科学这个大领域分成6块:
-
数据探索和准备;
-
数据表示和变换;
-
数据编程计算;
-
数据建模;
-
数据可视化和展示;
-
数据科学的科学。
而一个合格的数据科学家,应该掌握这6个子领域的相关技能。
数据科学家需要的技能
在之前介绍北美各种和数据分析相关职位要求的时候,从技术层面上列举了一些数据科学家需要的技能。现在进一步讨论下这个职业需要的不同方面技能。
首先谈谈数据科学家的教育背景。数学、统计、计算机或其他定量分析学科(电子工程,运筹学等)的本科以上学历是必需的。
根据2015年的统计数据,美国的数据科学家48%有博士学位,44%有硕士学位,只有8%是本科。研究生博士期间的课题最好偏向机器学习、数据挖掘或预测模型。其次需要数据库操作技能,在工作中通常需要用SQL从数据库读取数据。所以能熟练使用SQL是基础。对于统计或者数学专业的学生,在校期间可能不需要使用SQL,因此不太熟悉。这没有关系,我也是工作以后才开始使用SQL的。但你要确保自己至少精通一种程序语言,之后遇到需要用到的新语言可以迅速学习。在学校期间的主要目的不是学会毕业后所需的全部技能,这是不可能完成的任务。
高等教育(本科、研究生和博士)后应该具有的是基本的专业知识和自学能力。数据科学和很多其他领域一样,需要终身学习。有很多人问,要成为优秀的数据科学家是不是一定需要博士?这个问题很难用简单的是或者不是来回答。我看到的大多数优秀数据科学家确实都有博士学位,其余也都是硕士。我并不是要说高学历是成为优秀数据科学家的必要条件,其实真正重要的不是那个学历本身,而是拿到那个学历的过程,以及会选择获得这些学位的人共有的一些特质。
在美国,一般情况下,如果你拿到数理专业的博士学位,至少说明一个问题,就是你对学习的东西有兴趣。这样成天在电脑前面分析数据、编写程序的生活,对于那些对此不感兴趣的人来说必定是难以想象的痛苦。其次是研究生期间系统的理论训练。很多人可能觉得模型背后的数理知识不重要,只要会用模型就可以。统计软件使得很多模型使用者不需要知道具体的模型原理。了解模型原理是否能够帮助你更好地使用模型?当然会有帮助。但问题是这个帮助有多大?是不是值得我们花几年时间去学习?学习很多东西的好处是很难用短期去衡量的。我没有严格的分析,只是个人觉得了解模型原理是必要的。我很喜欢一个词“匠人精神”,也很乐意将“数据科学家”称为匠人,这是一种精益求精的精神。当然这种精神和学位没有必然联系,有本科毕业而对数据科学很感兴趣,自己学习也能够对这个学科有很深的理解。但大多数对这个领域感兴趣又具有“匠人精神”的人都有相关领域的更高等学历。最后,当然就是学习的能力。即使拿到博士学位,也不意味着学完了所有知识,而是具备了进一步自学的能力,可以自己看懂数据分析新方法的论文,也就是具备了在这个领域发展的自学能力。总的来说,这个领域的高学历现象并不能说明学历是必要条件,也不是充分条件。真正重要的是兴趣、匠人精神和自学能力。
编程能力也是数据科学家需要的基本技能。熟练使用一种编程语言是必需的,如R,Python,C等。有人可能会问,只会SAS够不够?个人意见是:不够。这里不想对SAS进行过多评价。我的建议是大家至少要熟悉一门开源语言。当然,这些都只是工具,工具是解决问题的手段,而非目的。你必须要有一个能用来进行数据分析的工具,偏好因人而异,但你选择工具的时候最好考虑工具的灵活性和可扩展性。
接下来就要提到具体的分析技能。数据科学家应该掌握高等概率统计,能够熟练进行t检验、开方检验、拟合优度检验、方差分析;能够清楚地解释Spearman秩相关和Pearson相关之间的区别。熟悉抽样,概率分布,实验设计相关概念;了解贝叶斯统计(很快就能在白板上写下贝叶斯定理);知道什么是有监督学习,什么是无监督学习;知道重要的聚类、判别和回归方法;知道基于罚函数的模型,关联法则分析。如果从事心理相关的应用的话(如消费者认知调查),还需要知道基本的潜变量模型,如探索性因子分析,验证性因子分析,结构方程模型。这个单子还可以一直列下去。看起来是不是不只一点吓人?我说过,数据科学家不是一个低门槛的行业,之前需要接受的训练对于没有兴趣的人来说是无比痛苦的。还有,单子是动态的,因为你在工作过程中还需要不断学习。这些技能只是让你能够很好地开始。再次强调自学能力和成为一个终生学习者是优秀的数据科学家的必要条件。
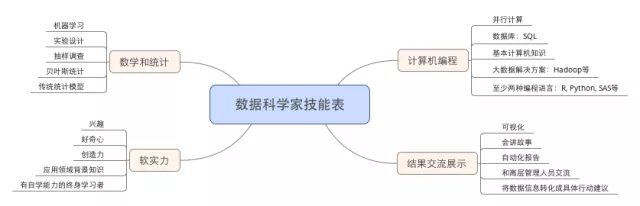
除了技术能力以外,还需要其他一些非技术的能力。这些包括将实际问题转化成数据问题的能力,这一过程需要交流,也就要求良好的交流沟通能力。关注细节,分析是一个需要细心和耐心的职业。还有就是展示结果的能力,如何让没有分析背景的客户理解模型的结果,并且最终在实践中应用模型的结论。如图1-2所示的“数据科学家技能表”中总结了数据科学家需要的各方面技能。
图1-2
总而言之,关于数据科学家有三个关键词:数据、科学和艺术。数据是基础;科学是工具;艺术是纽带。最终通过艺术将数据和科学结合得出的结果转化成相关领域的可应用知识,解决问题,真正产生价值。在实际应用中,以需要解决的问题为导向的思维方式很重要,否则分析很容易沦落为手段淹没目的的过程,很多分析行业的人就会犯这个错误,一味追求高大上的模型,酷炫的可视化,而忘了分析的根本目的是为了解决问题。说到这里,大家应该对这个行业有了一些概念性的了解了,可能有读者会问:你这么强调数据科学是为了解决问题的,那么都解决哪些问题呢?我们在接下来的小节会介绍数据科学家都使用什么技术,解决哪些问题。
在此之前,插播下数据科学家和数据工程师的区别。因为这两个角色确实很令人混淆,他们之间的合作最密切,而且其合作的融洽度在很大程度上决定了数据科学在组织内能否高效产生价值。这两个角色的区别当然在某种程度上和具体工作环境有关。比如在互联网行业,这两个角色重叠的部分更多。在传统行业各自的职责更加明晰。数据科学家需要知道数据能解决哪些问题,需要哪些数据以及用什么方法解决这些问题。找到问题的答案需要统计、机器学习等相关知识,在需要的时候,数据科学家得很快学会新的模型方法,以及如何用计算实施。这也是为什么数据科学家也要具备一定编程能力的原因,包括R、Python和MySQL。数据科学家和数据工程师区别的形象表示如图1-3所示。
图1-3
数据工程师能够让数据科学家更加高效的工作。有的公司也会将其称为数据构架师。他们收集、储存数据,对数据进行批量处理或者实时处理。有的公司的数据科学家通过API获取数据,这样更容易不需要使用SQL。但也有很大一部分公司的科学家是通过SQL获取数据,这样有更高的灵活度,也更利于两者的合作。当前有很多大数据的工具可以用于收集、储存和处理数据,数据工程师的重要职责之一是选择好的工具,这里需要能够用专业知识有理有据地支撑这个选择,而不是选择当前最流行的。因此数据工程师需要有很强的软件工程相关知识,他们不仅仅要能够学习如何使用这些工具,也要能够在必要的时候优化这些工具。一个好的数据工程师需要精通数据库和强大的工程实践能力,包括处理和记录错误、检测系统、设计具有容错能力的数据管道,理解如果要对当前构架进行扩展需要什么(为日后可能的新数据做准备),并且要持续处理各种可能的系统整合,数据库管理、清理和维护,保证数据管道(如图1-4所示)通向的是想要达成的目标。
图1-4
这两者之间也会有重叠的地方,比如数据科学家可能也会使用Hadoop生态群来解决某些数据问题,而数据工程师有时也可能在Spark集群上运行机器学习算法。最好的情况是这两个角色都能在一定程度上了解对方的技能,这样对他们之间的合作有极大的帮助。可以这样比喻,数据工程师是提供建房材料的人,而数据科学家是那个造房子的人。这样可能就很容易理解为什么这两者之间的合作对于一个成功的数据科学团队来说如此重要了。如果没有很好的沟通,建房的材料不符合房子建造者的需要,那即使建造者技术再好,也很难建造出好的房子,而且造成资源的极大浪费。
数据科学算法总结
在本小节中,我希望给大家总结一下数据科学的各种算法。这里的总结参考了Jason Brownlee的博文A Tour of Machine Learning Algorithms(http://machinelearningmastery.com/a-tour-of-machine-learning-algorithms/)。在该博文列出的类别框架下加减模型,并给出了额外的说明。这里根据算法的功能和形式对其进行了大致的归类。比如将树模型(Tree Model)归为一类,受神经网络(Neural Network)启发得到的模型。这样有助于给大家提供一个更大的框架,但这里的分类也并不是完美的。有的模型可能可以归为多类,比如支持向量机(Support Vector Machine)可以用于判别,也可以用于回归。因此,你可能会看到其他的分组方式。下面的总结也不可能列出所有的算法,由于个人知识有限,如果有遗漏的重要算法,欢迎大家反馈。因为书的篇幅所限,之后具体的模型技术章节中不会讲到所有的模型,而只是挑选其中我觉得最重要的进行更详细的介绍。
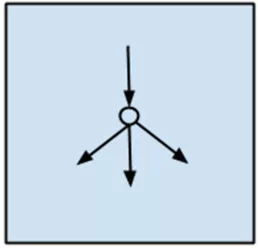
回归算法(Regression)
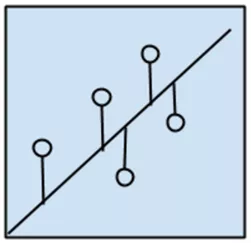
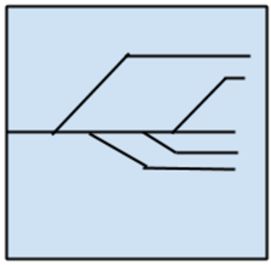
回归算法的示意如图1-5所示。
图1-5
回归可以指代算法,也可以指代某类问题。如之前提到的因变量为连续型的问题。作为算法通常指的是那类基于误差对自变量和因变量之间关系进行建模的方法。回归在统计学中应用极其广泛,所以通常称其为统计机器学习方法。常见的回归模型有:
-
一般最小二乘回归(Ordinary Least Squares)
-
逻辑回归(Logistic Regression)
-
自适应样条回归(Multivariate Adaptive Regression Splines,MARS)
-
局部估计散点图平滑回归(Locally Estimated Scatterplot Smoothing,LOESS)
最小二乘回归和逻辑回归大家应该不会陌生,这两个模型都是传统的统计回归模型,模型容易解释。MARS与神经网络和偏最小二乘类似,利用代理的特征来取代原始的预测变量。MARS 通过一个截断点将每个预测变量拆成两组,然后在每一组中建立预测变量与因变量的线性关系。MARS 模型共有两个调优参数:添加进模型的特征和阶数。结束和变量个数越多,模型越复杂,效果可能变好,但是可解释性一定变差。而LOESS是非参数模型,无法解释参数意义,通常只是在可视化中用到。
基于相似性的模型(Instance-based Algorithms)
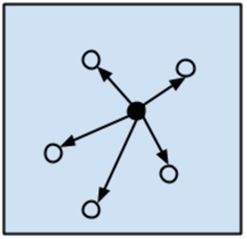
其于相似性的模型示意图如图1-6所示。
图1-6
这类模型通常基于某种相似性度量。将新样本和已有的样本比较,寻找和其最相近的,然后用这些相似样本的取值作为新样本取值的预测。这类模型也称为赢者通吃(winners take all)模型。这类模型的关键在于寻找合适的距离度量:
-
K近邻模型(k-Nearest Neighbour [KNN])
-
学习向量量化(Learning Vector Quantization [LVQ])
-
自组织映射(Self-Organizing Map [SOM])
这类模型的优点就是理解起来简单。麻烦在于要选择合适的距离度量。其中K近邻模型用得最多,另外两种很少听说。大家可能发现,将这些模型名翻译成中文有的让人感觉很奇怪,所以这里的中文只是供大家参考。
特征选择算法(Feature Selection Algorithms)
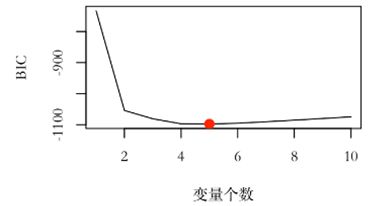
特征选择算法的示意图如图1-7所示。
图1-7
特征选择的主要目的是删除无信息变量或冗余变量,从而达到降维的效果。虽然所有自变量对于解释因变量来说都是重要的这种情况可能发生,但更常见的是因变量只和一部分自变量有关。我们会在之后的第8章,特征工程对特征选择详细展开:
-
过滤法(filter)
-
绕封法(wrapper)
-
内嵌法(embedded)
过滤法主要侧重于单个特征和目标变量的关系,在建模前对每个特征(或者自变量)进行评估,选择“重要”的变量进行建模。然后将模型评估结果作为需要优化的输出。
绕封法按照一定规律不断增加或者删除变量,通过评估不同特征组合得到的模型拟合结果寻找能够最优化模型拟合的特征组合。其本质是搜索算法,将不同的特征子集当作输入。
内嵌法是将特征选择的过程内嵌入建模的过程,它是学习器自身自主选择特征,如lasso,或者使用决策树思想的方法。
所有特征选择的方法都是建立在特定模型评估度量的基础上,在第7章“模型评估度量”会详细介绍所有常用的模型度量方法。
收缩方法(Regularization Methods)
收缩方法的示意图如图1-8所示。
图1-8
这类方法自身并不是一个完整的模型,而是衍生其他模型(比如回归模型)的方法。其本质就是在原来模型估计变量使用的准则(如似然函数值或者误差)上附加罚函数,对模型的复杂度进行惩罚,从而收缩模型参数,因此叫作收缩方法。这类方法在实践中很有效。我们在后面的章节会对此详细展开讨论。
-
岭回归(k-Nearest Neighbour,KNN)
-
LASSO回归(Least Absolute Sprinkage and Selection Operator)
-
弹性网络(Elastic Net)
上面的方法背后的原理是一样的,只是使用的罚函数不一样。具体会在之后的章节介绍。
树模型(Decision Tree)
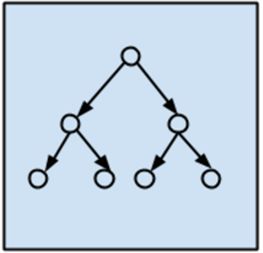
树模型的示意图如图1-9所示。
图1-9
这类模型不用我说,大家都该听过一万遍了。它们毫无疑问是使用最多的。为什么?因为实在太容易用,几乎不需要任何理论背景,效果又还过得去。下面是一些常见的树模型:
-
分类和回归树(Classification and Regression Tree,CART)
-
ID3(Iterative Dichotomiser 3)
-
C4.5
-
随机森林(Random Forest)
-
随机助推(Gradient Boosting Machines,GBM)
贝叶斯模型(Bayesian)
贝叶斯模型的示意图如图1-10所示。
图1-10
这里有个普遍的误解就是将使用贝叶斯定理的模型视为贝叶斯模型。其实很多基于概率理论的推断也会使用贝叶斯定理。这里将错就错,把数据科学领域普遍认为的贝叶斯模型归为一类。
-
朴素贝叶斯(Naïve Bayes)
-
平均单依赖估计(Averaged One-Dependence Estimators,AODE)
-
贝叶斯网络(Bayesian Belief Network,BBN)
核函数算法(Kernel Methods)
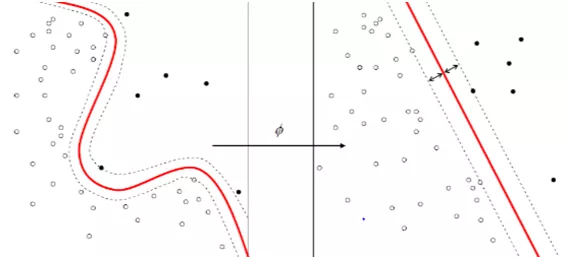
核函数算法的示意图如图1-11所示。
图1-11
核函数算法中最常见的是支持向量机(SVM)。这类算法把输入数据映射到一个高阶的向量空间,有些分类或者回归问题在新空间中更容易解决。
-
支持向量机(Support Vector Machine,SVM)
-
径向基函数(Radial Basis Function,RBF)
-
线性判别分析(Linear Discriminate Analysis,LDA)
聚类算法(Clustering Methods)
聚类算法的示意图如图1-12所示。
图1-12
聚类,就像回归一样,有时候人们描述的是一类问题,有时候描述的是一类算法。聚类算法通常按照中心点或者分层的方式对输入数据进行归并。所以聚类算法都试图找到数据的内在结构,以便按照最大的共同点将数据进行归类。
常见的聚类算法包括K-Means算法和分层聚类两类。
-
K-Means
-
分层聚类(Hierachical Clustering)
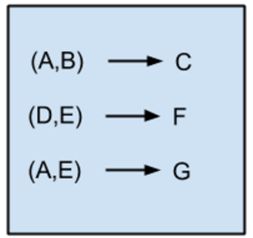
关联法则(Association Rule)
关联法则的示意图如图1-13所示。
图1-13
关联法则挖掘的基本想法是:当若干事件共同发生的频率大于某人仅从它们各自单独发生的频率出发预期的共同发生率时,此共同发生的情况即为一个令人感兴趣的模式。关联法则通常用于商业购物篮分析。也就是看消费者更可能将哪些商品放在一个购物篮里,可以优化超市货架布局。比如,如果发现客户买土豆的时候总是会顺带买牛肉(可能是土豆炖牛肉),那么就可以在牛肉的售货区也摆放一些土豆。或者在土豆的货架旁放置牛肉促销的信息。常见算法有:
-
Apriori算法
-
Eclat算法
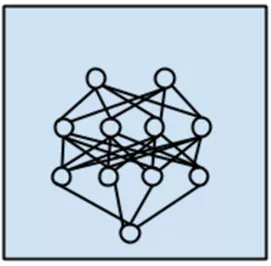
人工神经网络(Artificial Neural Network)
人工神经网络的示意图如图1-14所示。
图1-14
神经网络是一种强大的非线性回归方法,它受大脑的工作原理启发而来,模拟生物神经网络,是一类模式匹配算法。与偏最小二乘类似,因变量利用一系列中间层的非观测变量(称为隐藏变量或隐藏元)进行建模,可以用于解决分类和回归问题。人工神经网络是机器学习的一个庞大的分支,有几百种不同的算法(深度学习就是其中的一类算法,后面会单独列出)。
-
感知器神经网络(Perceptron Neural Network)
-
反向传递(Back Propagation)
-
Hopfield网络(Hopield Network)
-
自组织映射(Self-Organizing Map,SOM)
-
学习矢量量化(Learning Vector Quantization,LVQ)
深度学习(Deep Learning)
深度学习的示意图如图1-15所示。
图1-15
这又是一个过度炒作,让人不明觉厉的主儿。深度学习这个名字极具误导性,更准确的说法其实是深度神经网络。就是之间的人工神经网络多加一些中间层。这类算法在AlphaGO战胜李世石之后有一举成名的感觉。很多深度学习的算法是半监督式学习算法,用来处理存在少量未标识数据的大数据集。
-
受限波尔兹曼机(Restricted Boltzmann Machine,RBN)
-
深度网络(Deep Belief Networks,DBN)
-
卷积网络(Convolutional Network)
-
堆栈式自动编码器(Stacked Auto-encoders)
降维算法(Dimensionality Reduction)
降维算法的示意图如图1-16所示。
图1-16
其本质是用不同变量的组合代替原变量的技术。它的目的是自动地构建新的特征,将原始特征转换为一组具有明显物理意义或者统计意义的特征。比如通过变换特征取值来减少原始数据中某个特征的取值个数等。
-
主成分分析(Principle Component Analysis,[PCA)
-
偏最小二乘回归(Partial Least Square Regression,PLS)
-
高维标度化(Multi-Dimensional Scaling,MDS)
-
探索性因子分析(Explortary Factor Analysis,EFA)
主成分分析(PCA)试图找到原变量的不相关线性组合,这些线性组合能够最大限度地解释原数据中变量方差。探索性因子分析(EFA)同样试图在尽量小的维度上解释原数据中尽可能多的方差。高维标度化(MDS)将观测到的相似度映射到低维度上,如二维平面。MDS能够作用于非数值型变量,如分类变量或者有序数据预测变量。EFA的目标是找到能最大限度解释显变量方差的隐因子(即潜变量)。
集成算法(Ensemble Methods)
集成算法的示意图如图1-17所示。
图1-17
在20世纪90年代,集成方法(即将许多模型组合起来进行预测的模型)开始出现。但当样本量n较之于变量个数p而言比较大时,该方法可以作为降低模型方差的一般方法。装袋法(Bagging,bootstrap aggregation 的缩写)最初由 Leo Breiman 提出,它是最早发展起来的集成方法之一。之后又有了随机森林和助推法。关于集成方法我们会在后面的章节详细介绍,其本质就是将一系列弱学习器的结果整合起来。这是一类非常强大且有效的算法。
-
装袋法(Bootstrapped Aggregation,Bagging)
-
随机森林(Random Forest)
-
梯度助推(Gradient Boosting Machine [GBM])
数据科学可以解决什么问题
前提要求
数据科学不是万能药,数据科学家也不是魔术师,有些问题我们无法用数据科学解决,最好在一开始就对问题做出判断,对于那些无法解决的问题,诚实地告诉对方并解释原因。那我们对问题有什么要求呢?
你的问题需要尽可能具体
来看两个例子。
-
问题1:如何提高产品销售量?
-
问题2:今年年初推出的新促销手段是不是提高了先锋先玉696玉米种子在西南地区的销售量?
比较上面这两个问题,大家是不是很快能发现它们的差别?问题1从语法上是个正确的问题,但从解决的角度,并不是一个能够用分析给出答案的问题。为什么?因为问题太泛了,根本无从定义该问题背后的自变量和因变量。而问题2就是一个恰当的问题。
从分析的角度,因变量很明显是“先锋先玉696玉米种子在西南地区的销售量”,感兴趣的自变量是“今年年初推出的新促销手段”,我们想要研究的就是这两者之间的关系。从这里开始再去寻找其他变量,这样就慢慢地进入分析流程了。当然,问题具体不代表就能够回答。比如我曾经遇到一个很具体的供应链问题,问的是针对某一个特定产品在特定区域的库存该是多少。
这个问题为什么无法回答呢?这个项目一开始我通过多元自适应回归样条(MARS)模型以为找到了一个合理的答案,但到项目的最后才发现,他们给我的供应相关的数据极其不准确,很多地区的供应量都只是估计。这是我从业生涯中的一次教训,这告诉我们下面将要提到的一点。
你要有和问题相关的必要数据
巧妇难为无米之炊,这句古人的话放在那里时刻闪闪发光。艺术源于生活,所以你首先得要有数据,之所以数据科学会火也是因为计算机的发展,使数据的收集更容易。上面提到的供给问题就是一个很好的例子,没有相对准确的数据,之后任何模型都没有意义。当然,任何数据都是存在误差的,但是误差必须在一定范围内。尤其是感兴趣的自变量(如之前问题2里的“新促销手段”相关的数据)和因变量(“先锋先玉696玉米种子在西南地区的销售量”),如果这些必要的变量有很大缺失,或者不准确的话,模型是无法发挥作用的。再如,你要预测某个产品的消费者中谁最可能在接下来的3个月内购买该产品。要解决这个问题,你需要有目标消费者群体历史购买行为的信息:上一次购买的时间,消费量,优惠券使用情况等等。如果你仅仅知道这些客户的银行卡号,身份证号,出生月份之类的信息是不会对你的预测有任何帮助的。
很多时候数据的质量比数量更重要,但数量也是不容忽视的。在能保证数据质量的前提下,数量越多越好。样本量越大,你能够回答的问题也就越细,且模型发现的置信度也更高。如果你有一个具体合理的问题,有足够大、质量合理的相关数据集,那么恭喜你,可以开始玩数据科学啦!
问题种类
很多数据科学的书籍都从技术的角度对各种模型分类。比如有监督模型和无监督模型,线性模型和非线性模型,参数模型和参数模型,等等。这里我们换而使用之前提到的“问题导向”的思维方式,对数据科学回答的问题进行分类,然后介绍哪些模型可以用于回答相应类别的问题,希望这些分组能在你面对自己的问题时帮助思考,如图1-18所示。
图1-18
比较
第一类常见的问题是比较组之间不同的问题。常见的句式是:A在某方面是不是比B好?或者多者比较:A、B、C之间在某方面有没有差别?下面是一些问题的例子:
-
参与促销活动和没有参与促销活动消费者购买量有差异吗?
-
男性是不是比女性更倾向于购买我们的产品?
-
用户满意度在不同商业区是不是不同?
-
服用某种药物的老鼠比没有服用药物的老鼠体重增长得是否更快?
-
携带某种基因的大豆是不是比普通大豆产油量高?
对于这类数据,通常从各组观测的基本统计量和可视化开始初步探索数据。在对数据分布和组之间的差异有个初步直观了解之后,通过统计检验测试组间是否在感兴趣的变量上有显著不同。处理这类问题常用的是经典统计推断:开方检验、t检验和方差分析。放在贝叶斯框架下也有一种比较组间不同的方法。如果因子增加,结构变得复杂(如在生物医药领域的复杂实验设计有随机效应因子),则需要使用更加复杂的混合效应模型。
描述
在分析中不可避免地要描述数据。比如聚类问题。当你通过算法找到不同的样本分类后,就需要对类进行定义,这要通过比较各类中变量的描述统计量得到。常用的描述问题有:
-
样本中家庭年观测的收入是不是无偏的?
-
某产品在不同区域的月销售量均值/方差是多少?
-
变量的量级差异大吗?(决定是否需要对数据标准化)
-
模型中的预测变量观测缺失情况如何?
-
问卷调查回复者的年龄分布范围是什么?
这类数据描述常用于检查数据,找到合适的数据预处理方法,以及拟合模型后对结果的分析和展示。
聚类
聚类是一个极其常见的问题,其通常和判别联系在一起。聚类模型回答的问题是:
-
哪些消费者有相似的产品偏好?(市场营销)
-
哪些打印机损坏的模式相同?(质量控制)
-
公司员工在对公司评价上可以分为几类?(人力资源)
-
哪些词更经常同时出现?(自然语义处理)
-
哪些文档可能有相似的主题?(自然语义处理)
需要注意的是,聚类是无监督分析。
判别
判别是另外一个经典的分析问题。通常用类别已知的样本作为训练集拟合判别器,然后用训练好的判别器预测新样本的类别。下面是一些关于判别的问题:
-
哪些新客户最有可能转化(购买)?
-
当前的压力度数是正常的吗?
-
某贷款人有不还款的风险吗?
-
这个消费者还可能喜欢什么产品?
-
这本书的作者可能是谁?
-
这封邮件是不是垃圾邮件?
关于判别的模型有数百种,在实践中我们其实不必要尝试所有的模型,而只要拟合其中几种在大部分情况下表现最好的模型即可。我们在后面判别的章节还会介绍。
回归
当你感兴趣的量是一个数值而非类别时,通常就是一个回归问题。比如:
-
明天的气温可能会是多少?
-
公司今年第4季度的销售额会是多少?
-
某品牌打印机明年上半年在北京市的销量会是多少?
-
该引擎还能工作多久?
-
这次活动中需要准备多少啤酒?
通常情况下,回归能够给出一个数值答案。回归通常解决“……是多少?”这样的问题。在有些时候模型给出的负数结果可能需要解释为0,或者有小数点的结果需要解释为最近的整数。
小结
在本章中,我们对数据科学和数据科学家进行了总体介绍。希望在各种炒作当中还原一个相对真实的数据科学家。数据科学是否有泡沫?
我认为,虽然过度炒作但是没有泡沫。因为现在很多公司,尤其是传统公司并没有开始真正应用数据科学。而数据科学本身在这物联网的时代无疑是公司要有竞争力必不可少的。
这其实不是一门全新的学科,而是一个旧学科的新组合。希望大家在阅读了本章之后对数据科学的能力和局限有更好的了解。对于想成为数据科学家的读者,希望你们能更清楚这门行业需要的技能背景,完善自己的各种能力。
编者按:本书的写作对象是那些现在从事数据分析相关行业,或者之后想从事数据分析行业的人,意在为实践者提供数据科学家这门职业的相关信息。读者可以从阅读中了解到数据科学能解决的问题,数据科学家需要的技能,及背后的“分析哲学”。对于新手而言,一开始就直奔艰深的理论,很容易因为困难而失去兴趣最终放弃。因此本书倡导的是一种循序渐进的启发教学路径,着重在于数据科学的实际应用,让读者能够重复书中的结果,学习数据分析技能最好的方式是实践!希望笔者在北美从事数据科学工作多年踏遍大大小小不计其数的坑换来的经验,能够帮助读者更加顺利地成为数据科学家!