python怎么计算相关系数、偏相关系数？

首先看下相关系数、偏相关系数的计算公式

Xi=[1.1, 1.9, 3]
Yi=[5.0, 10.4, 14.6]
E(X) = (1.1+1.9+3)/3=2
E(Y) = (5.0+10.4+14.6)/3=10
E(XY)=(1.1×5.0+1.9×10.4+3×14.6)/3=23.02
Cov(X,Y)=E(XY)-E(X)E(Y)=23.02-2×10=3.02
此外：还可以计算：
D(X)=E(X²)-E²(X)=(1.1²+1.9²+3²)/3 - 4=4.60-4=0.6 σx=0.77
D(Y)=E(Y²)-E²(Y)=(5²+10.4²+14.6²)/3-100=15.44 σy=3.93
X,Y的相关系数：
r(X,Y)=Cov(X,Y)/(σxσy)=3.02/(0.77×3.93) = 0.9979

协方差与方差之间有如下关系：
D(X+Y)=D(X)+D(Y)+2Cov(X，Y)
D(X-Y)=D(X)+D(Y)-2Cov(X，Y)
协方差与期望值有如下关系：
Cov(X，Y)=E(XY)-E(X)E(Y)。
协方差的性质：
（1）Cov(X，Y)=Cov(Y，X)；
（2）Cov(aX，bY)=abCov(X，Y)，（a，b是常数）；
（3）Cov(X1+X2，Y)=Cov(X1，Y)+Cov(X2，Y)。
由协方差定义，可以看出Cov(X，X)=D(X)，Cov(Y，Y)=D(Y)。
设X和Y是随机变量，若E(X^k)，k=1，2，...存在，则称它为X的k阶原点矩，简称k阶矩。
若E{[X-E(X)]k}，k=1，2，...存在，则称它为X的k阶中心矩。
若E{(X^k）（Y^p)}，k、l=1，2，...存在，则称它为X和Y的k+p阶混合原点矩。
若E{[X-E(X)]^k[Y-E(Y)]^l }，k、l=1，2，...存在，则称它为X和Y的k+l阶混合中心矩。
显然，X的数学期望E(X)是X的一阶原点矩，方差D(X)是X的二阶中心矩，协方差Cov(X，Y)是X和Y的二阶混合中心矩。

再看看偏相关系数的计算公式

python实现

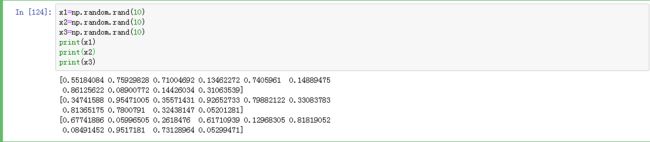
x1=np.random.rand(10)
x2=np.random.rand(10)
x3=np.random.rand(10)
print(x1)
print(x2)
print(x3)

# 利用pandas
df=pd.DataFrame([x1,x2,x3],index=['a','b','c']).T
print('数据:\n',df)
print('相关系数矩阵为：\n',df.corr())
r_ab=df.a.corr(df.b)
r_ac=df.a.corr(df.c)
r_bc=df.b.corr(df.c)
r_ab_c=(r_ab-r_ac*r_bc)/(((1-r_ac**2)**0.5)*((1-r_bc**2)**0.5))
print('ab_c的一阶偏相关系数为：',r_ab_c)

# 利用Numpy
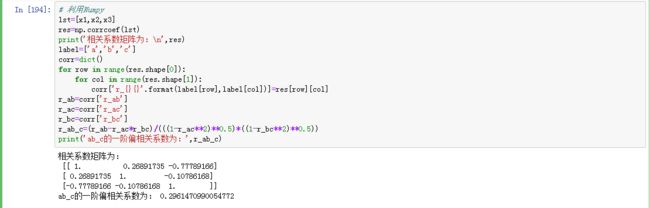
lst=[x1,x2,x3]
res=np.corrcoef(lst)
print('相关系数矩阵为：\n',res)
label=['a','b','c']
corr=dict()
for row in range(res.shape[0]):
    for col in range(res.shape[1]):
        corr['r_{}{}'.format(label[row],label[col])]=res[row][col]
r_ab=corr['r_ab']
r_ac=corr['r_ac']
r_bc=corr['r_bc']
r_ab_c=(r_ab-r_ac*r_bc)/(((1-r_ac**2)**0.5)*((1-r_bc**2)**0.5))
print('ab_c的一阶偏相关系数为：',r_ab_c)

# 利用sicpy
from scipy import stats
r_ab=stats.pearsonr(x1,x2)[0]
r_ac=stats.pearsonr(x1,x3)[0]
r_bc=stats.pearsonr(x2,x3)[0]
r_ab_c=(r_ab-r_ac*r_bc)/(((1-r_ac**2)**0.5)*((1-r_bc**2)**0.5))
print('ab_c的一阶偏相关系数为：',r_ab_c)

# 自己写公式
import math
def calc_corr(a,b):
    E_a = np.mean(a)
    E_b = np.mean(b)
    E_ab=np.mean(list(map(lambda x:x[0]*x[1],zip(a,b))))

    # 计算分子，协方差—cov(a,b)=E(ab)-E(a)*E(b)
    cov_ab = E_ab - E_a * E_b

    def square(lst):
        res=list(map(lambda x:x**2,lst))
        return res
    
    # 计算分母，D(X)=E(X²)-E²(X)
    D_a=np.mean(square(a))-E_a**2
    D_b=np.mean(square(b))-E_b**2

    σ_a=np.sqrt(D_a)
    σ_b=np.sqrt(D_b)
    
    corr_factor = cov_ab / (σ_a*σ_b)
    return corr_factor

r_ab=calc_corr(x1,x2)
r_ac=calc_corr(x1,x3)
r_bc=calc_corr(x2,x3)
r_ab_c=(r_ab-r_ac*r_bc)/(((1-r_ac**2)**0.5)*((1-r_bc**2)**0.5))
print('ab_c的一阶偏相关系数为：',r_ab_c)