机器学习笔记（11）——关联分析之Apriori算法原理和Python实现

说到关联分析，首先想到的就是“啤酒和尿布”的案例，那么如何发现“啤酒”和“尿布”之间的关联关系呢，就是寻找频繁项集。先来学习两个概念。

1、支持度和可信度

支持度（support）——数据集中包含该项集的记录所占的比例。

可信度（confidence）——针对一条关联规则定义，如{尿布}--->{啤酒}的可信度为“支持度（{尿布，啤酒}/支持度（{尿布}））”。

例如：支持度（{尿布，啤酒} = 3/5，支持度（{尿布}）=4/5，那么可信度（{尿布}--->{啤酒}）=0.75，说明购买“尿布”的订单中有75%的购买了“啤酒”。

支持度和可信度是量化关系分析是否成功的方法。假设想找到支持度大于0.8的所有项集，一个办法就是生成所有可能组合的清单，然后对每一种组合统计出其频繁程度，但如果物品多时，速度会非常慢。Apriori原理则可以减少关联规则学习时的计算量。

2、Apriori原理

假设有4种商品，这些商品的组合可能只有1种，也可能是2种、3种或4种，那么所有可能的组合数为

对于有N种物品的数据集，共有种项集组合。即使只出售100种商品，也会有种可能的项集组合，计算量非常大，更何况100种商品并不算多。

Apriori原理是指如果某个项集是频繁的，那么它的所有子集也是频繁的。反过来看，如果一个项集是非频繁的，那么它的所有超级也是非频繁的。

例如，项集{2,3}是非频繁的，那么{0,2,3}，{1,2,3}，{0,1,2,3}也是非频繁的，就不用计算他们的支持度了。这样就可以降低计算量。

 

关联分析的包括两项：发现频繁项集和发现关联关系，首先要找到频繁项集，然后从中获得关联关系。

3、使用Apriori算法发现频繁集

Apriori算法有两个输入参数，分别是最小支持度和数据集。

（1）首先会生成单个物品的项集列表。

（2）接着扫描交易记录，查看哪些项集满足最小支持度，把不满足的集合去掉。

（3）然后对剩下的集合进行组合，生成包含两个元素的集合。

（4）再扫描交易记录，去掉不满足最小支持度的项集。

（5）重复以上过程，直到所有项集都被去掉。

先创建几个辅助函数：

# 加载数据集
def loadDataSet():
    return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]

# 构建大小为1的所有候选集的集合
def createC1(dataSet):
    C1 = []
    for transaction in dataSet:
        for item in transaction:
            if not [item] in C1:
                C1.append(([item]))
    C1.sort()
    return map(frozenset, C1)

# 返回满足最小支持度的项集，同时返回一个包含支持度值的字典。D数据集，Ck候选项集，minSupport最小支持度
def scanD(D, Ck, minSupport):
    ssCnt = {}
    DD = copy.deepcopy(D)  # python3.6中，map类型遍历后会变为“空”，因此为了能够再次遍历，需要深度复制一份
    CkCk = copy.deepcopy(Ck)
    for tid in D:
        for can in Ck:
            if can.issubset(tid):
                if can not in ssCnt:
                    ssCnt[can] = 1
                else:
                    ssCnt[can] += 1
        Ck = copy.deepcopy(CkCk)

    numItems = float(len(list(DD)))
    retList = []
    supportData = {}
    for key in ssCnt:
        support = ssCnt[key] / numItems
        if support >= minSupport:
            retList.insert(0, key)
        supportData[key] = support
    return retList, supportData

测试一下函数：

下面继续构建完整的Apriori算法。

# 构建候选集Ck
def aprioriGen(Lk, k):
    retList = []
    lenLk = len(Lk)
    for i in range(lenLk):
        for j in range(i + 1, lenLk):
            L1 = list(Lk[i])[:k - 2]
            L2 = list(Lk[j])[:k - 2]
            L1.sort()
            L2.sort()
            if L1 == L2:
                retList.append(Lk[i] | Lk[j])
    return retList

# 返回所有频繁项集，及其支持度
def apriori(dataSet, minSupport=0.5):
    C1 = createC1(dataSet)
    D = map(set, dataSet)
    D1 = copy.deepcopy(D)
    L1, supportData = scanD(D, C1, minSupport)
    D = copy.deepcopy(D1)  # D遍历后就变成空了，需要再次赋值，用于下一次遍历
    L = [L1]
    k = 2
    while len(L[k - 2]) > 0:
        Ck = aprioriGen(L[k - 2], k)
        Lk, supK = scanD(D, Ck, minSupport)
        supportData.update(supK)
        L.append(Lk)
        k += 1
        D = copy.deepcopy(D1)  # D遍历后就变成空了，需要再次赋值，用于下一次遍历
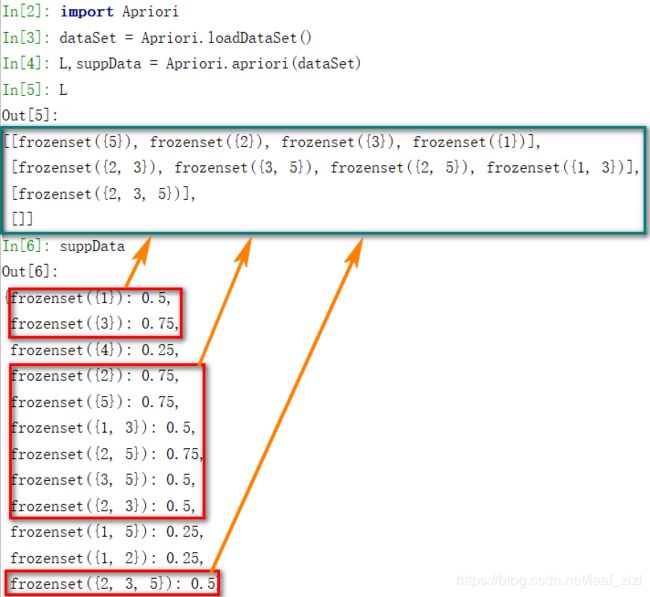
    return L, supportData

apriori()是主函数，返回符合最小支持度的频繁项集，它通过调用aprioriGen()来创建候选项集Ck。测试一下运行结果。

4、从频繁项集中挖掘关联关系

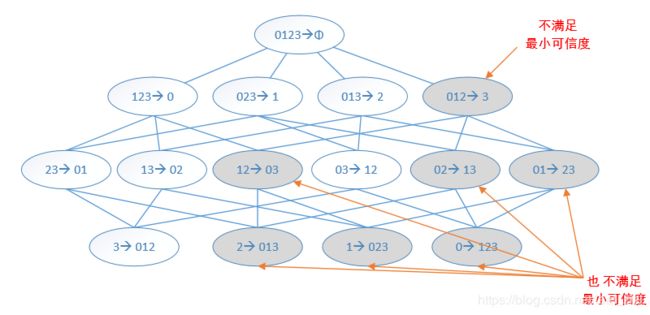
类似于频繁项集生成，可以为每个频繁项集生成多个关联规则，例如对频繁项集{0,1,2,3}，可以生成如下关联规则。

如果关联规则{0,1,2}--->{3}不满足最小可信度要求，那么任何左部为{0,1,2}的子集的规则也不会满足最小可信度，原因如下：

可信度（{0,1,2}--->{3}）=支持度（{0,1,2,3}）/ 支持度（{0,1,2}）

可信度（{0,1}--->{2,3}）=支持度（{0,1,2,3}）/ 支持度（{0,1}）

支持度（{0,1}）一定大于等于支持度（{0,1,2}），因此 可信度（{0,1}--->{2,3}）一定小于等于可信度（{0,1,2}--->{3}）

# 关联规则，参数：频繁项集、频繁项集支持度、最小可信度阈值，返回一个包含可信度的规则列表
def generateRules(L, supportData, minConf=0.7):
    bigRuleList = []
    for i in range(1, len(L)):  # 只取两个及以上元素的项集
        for freqSet in L[i]:
            H1 = [frozenset([item]) for item in freqSet]
            if (i > 1):  # 大于2个元素的项集，做进一步合并
                rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
            else:  # 2个元素的项集，计算可信度
                calcConf(freqSet, H1, supportData, bigRuleList, minConf)
    return bigRuleList

# 计算可信度，参数：频繁项、频繁项集字典、频繁项集支持度、关联规则列表、最小可信度阈值，返回满足最小可信度的规则列表
def calcConf(freqSet, H, supportData, brl, minConf=0.7):
    prunedH = []
    for conseq in H:
        conf = supportData[freqSet] / supportData[freqSet - conseq]
        if conf >= minConf:
            print (freqSet - conseq, '--->', conseq, '可信度：', conf)
            brl.append((freqSet - conseq, conseq, conf))
            prunedH.append(conseq)
    return prunedH


# 合并函数，对于多于2个元素的项集，做递归挖掘关联关系
def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
    m = len(H[0])
    if (len(freqSet) > (m + 1)):
        Hmp1 = aprioriGen(H, m + 1)
        Hmp1 = calcConf(freqSet, Hmp1, supportData, brl, minConf) # 返回满足最小可信度的关联关系
        if (len(Hmp1) > 1): # 如果满足最小可信度，再继续挖掘，否则子集也不会满足
            rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)

代码构建完成了，可以写个主函数来测试一下：

if __name__ == '__main__':
    dataSet = loadDataSet()
    L, suppData = apriori(dataSet, 0.5)
    rules = generateRules(L, suppData, 0.5)

结果如下，如果把最小可信度改为0.7，则最后只返回3条可信度为1.0的规则。

5、总结

学习关联分析，首先理解支持度和可信度两个概念，挖掘关联关系，就是在“较高”支持度的频繁项集中，发现“较高”可信度的关联关系。为了提高计算效率，利用Apriori原理，通过过滤非频繁项集及其超级来减少发现频繁项集的计算量，通过过滤不满足最小可信度的关联规则及其所有子集的关联规则，来减少发现关联关系的计算量。尽管如此，在数据集合较大时，Apriori算法的计算速度仍然会比较慢。

---

代码资源下载地址：

https://download.csdn.net/download/leaf_zizi/12084772

---

参考：

Peter Harrington 《机器学习实战》