图像处理【1】空间金字塔Lucas Kanade光流法

论文 Pyramidal Implementation of the Lucas Kanade Feature Tracker Description of the algorithm的阅读笔记。
光流法用途比较多，比如跟踪，图像配准，以及在三维人脸重建中的稠密对应。

问题描述

假设 I , J 是两张2D灰度图片， I(x)=I(x,y) , J(x)=J(x,y) 分别为坐标 x=[x,y] 上的像素值。

考虑图像 I 上的一点 u=[ux,uy]T ，那么特征跟踪的目的是在图像 J 找到点 v=u+d=[ux+dx,uy+dy]T ，使得 I(u) , J(v) 尽可能的一样。 d=[dx,dy]T 是图像在点 x 上的速度，也称光流。点 d 的求解定义在一个比较小的邻域内，通常是5*5。整个问题的表示可以用，求解以下损失函数：

ϵ(d)=ϵ(dx,dy)=∑x=ux−wxuX+wx∑y=uy−wyuy+wy(I(x,y)−J(x+dx,y+dy))2

其中邻域定义为 (2wx+1)∗(2wy+1) 。该损失函数的成立条件是，在同一个邻域内的点的光流是一样的。

算法

标准的光流法在处理运动幅度大的图片时，会出现问题。尽管可以使用大的窗口，但是大窗口会影响局部准确率。而基于图片空间金字塔的Lucas-Kanade则能够很好的处理该问题。

1、图片金字塔

图片金字塔是通过在原始图片上获取不同的分辨率而得到的。比如原始图片为1000*1000，金字塔有三层L=3，则最后的金字塔图片分辨率有：L0：1000*1000，L1：500*500,L2：250*250,L3：125*125。在缩小图片时，位置为x，y的像素值采用滤波的方式获取，如第L层中x，y的像素重第L-1层中的2x，2y坐标的领域获取：

这里边还要处理边界问题， nx , ny 分别是图片的最大长宽。超出边界的像素值用边界值代替：

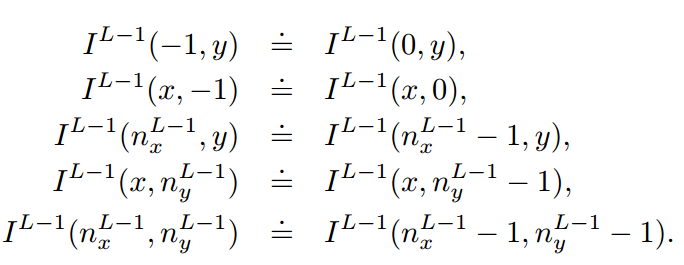
2、金字塔特征跟踪

求解最终的 d ，是通过从图像金字塔的最高层开始，也就是分辨率最低的图片，然后一直递归求解到原始图片。我们假设，第L层的损失函数为：

其中 gLx , gLy 是已知的用如下公式获取：

gL=2(gL+1+dL+1)

该公式是一个递归的过程，最高层的g=[0,0]，d则是利用标准的lucas-Kanade算法求解出来。
因此最终的

d=∑LmL=02LdL 。

3、迭代Lucas-Kanade算法

第L层中在以 [px,py] 为中心的邻域里点[x,y]的值可由下面的公式获取：

令 v⎯⎯=[vx,vy]T=dL ，则损失函数重写为：

为了最小化损失函数，我们有：

将 B(x+vx,y+vy) 进行泰勒展开，则有：

同时令：



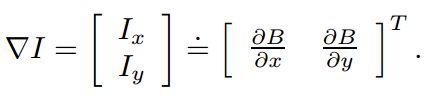
得出：

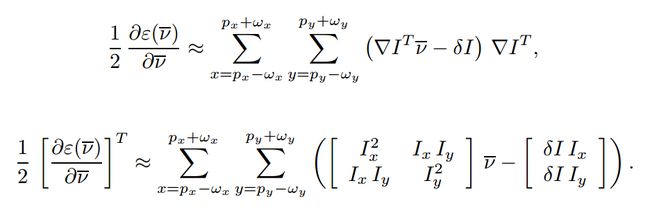
令：

最终可解出v：


以上是标准的Lucas-Kanade算法。

现在说一下迭代的Lucas-Kanade算法。
算法的主要思想是，在第k次迭代算法出v时；第k+1次的求解也是使用标准的Lucas-Kanade算法，只不过需要更新一下图像B的在点 [px,py] 上的邻域：

最终的v：

整个算法的推导大致是这样的。论文剩下的是算法的流程，以及一些细节处理，如亚像素计算。