Unity Shader:实现菲涅尔+色散效果的环境映射以及相关原理解析
文章目录
- 1,色散在光学中的原理
- 2,反射的数学计算方法以及用它实现环境映射
- 3,折射的原理以及色散的实现
- 4,菲涅尔效果
- 5,拥有菲涅尔与色散效果的环境映射
1,色散在光学中的原理
复色光
——现实生活中的许多光都是复色光,例如阳光。
光谱
——光学频谱,简称光谱,是复色光通过色散系统(如光栅、棱镜)进行分光后,依照光的波长(或频率)的大小顺次排列形成的图案。
https://zh.wikipedia.org/wiki/%E5%85%89%E5%AD%B8%E9%A0%BB%E8%AD%9C
色散
——复色光通过介质产生折射时,由于复色光中各个光的波长(影响折射率)不同而导致各个光线依次分开。
2,反射的数学计算方法以及用它实现环境映射
反射可以用来解释你在镜子或水面中看到的景象。将你看向镜面的视角抽象为一组向量,当这组向量接触到镜面后会生成一组反射向量,而这组反射向量再次接触到的点的集合既是你在镜面中所见的景象。
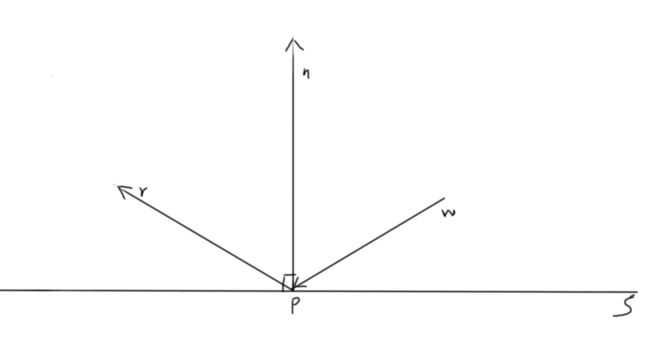
二维中看起来比较简单,w为入射向量,r为反射向量,S为反射介质,P为反射点,n垂直于S。只要做到w与s的夹角与r与s的夹角相等,既做到了反射。
但在三维中,是通过一系列向量运算来寻找反射向量的。
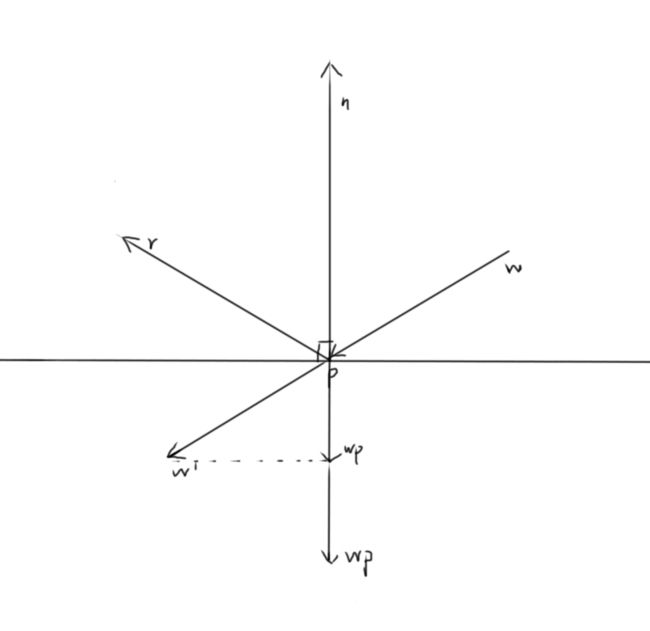
首先计算w的projection,并移到下方。视觉上理解既是将w移到w’处,n向下延伸,从w’做一条垂直于n的虚线,n的延伸与虚线的交点既是向量wp的终点,wp=dot(w,n/|n|),然后再做一条wp。在wp2的终点画一条’-w’,根据向量的加法法则,r’=wp2-w, -r’=r既是w的反射向量。
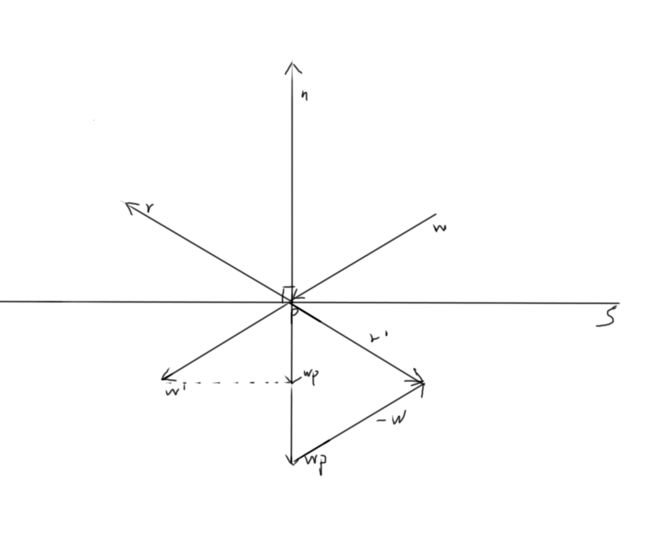
用数学公式表达则是:
wp=dot(w,n/|n|) , wp is the projection of w on n.
r’=wp*2-w
r=-r’
r既是w的反射向量
而在Shader中,以上这些计算过程都被封装进了一个方法:
float r=reflect(w,n);
天空盒是opengl立方体映射cube-map的一个典型应用,可以想象成有6个正方形2D纹理组成一个立方体cube包住了整个场景(下图中cube的四个边,图画的不准确四个边是等长的)。这个cube与视角的位置关系是固定的,camera永远都是在这个cube的中央。
环境映射是对天空盒进行采样后再次渲染。如果利用反射对天空盒进行立方体采样,可以模拟现实中的镜像效果(下图中摄像机在S平面上的P点可观察到天空盒R点上的颜色)。
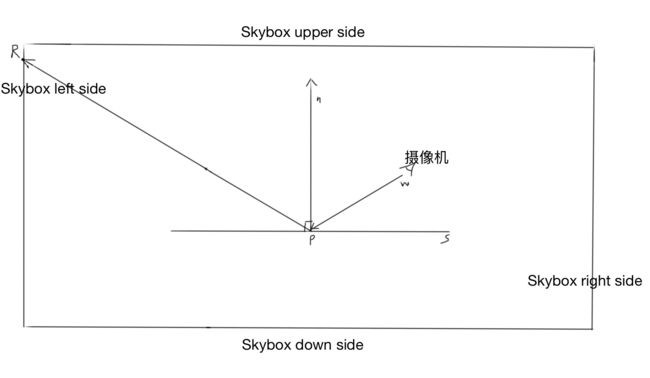
以下代码为Unity官网的环境映射示例Shader,将顶点着色器中的一些计算改到了在片段着色器中计算,优化计算精度。
Shader "Unlit/SkyReflection"
{
SubShader
{
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
struct v2f {
float3 normal:NORMAL;
half3 worldRefl : TEXCOORD0;
float4 pos : SV_POSITION;
float4 objectPOS:float;
};
v2f vert (float4 vertex : POSITION, float3 normal : NORMAL)
{
v2f o;
o.pos = UnityObjectToClipPos(vertex);
o.normal=normal;
o.objectPOS=vertex;
return o;
}
fixed4 frag (v2f i) : SV_Target
{
//i.normal既是上图中的n。
i.normal = UnityObjectToWorldNormal(i.normal);
//worldPos为上图中的P。
float3 worldPos = mul(unity_ObjectToWorld, i.objectPOS).xyz;
//worldViewDir为由P点射向camera的一条向量。
float3 worldViewDir = UnityWorldSpaceViewDir(worldPos);
//所以在reflect函数中要使用-worldViewDir,将方向颠倒过来,既成为了上图中的w。i.worldRefl既是
//上图中的r。
i.worldRefl = reflect(-worldViewDir, i.normal);
//进行立方体采样,既是根据上图中的r寻找立方盒上的点R。
half4 skyData = UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, i.worldRefl);
half3 skyColor = DecodeHDR (skyData, unity_SpecCube0_HDR);
fixed4 c = 0;
c.rgb = skyColor;
return c;
}
ENDCG
}
}
}
效果:

这里有一个细节,当利用反射进行环境映射时,有弧度的物体的效果要明显优于平面物体,因为有弧度的平面生成的反射向量角度更广更离散,插值后采样时覆盖的uv值更大,再渲染时模拟出的距离感更加真实(和近大远小的原理类似)。而平面物体生成的反射向量大部分都反射到了天空盒的一小部分区域,效果有点穿帮,源于这种反射"揭穿"了天空盒虚拟出的的无限远效果。

上图中球体换为立方体后只反射出星球的一小块区域。
3,折射的原理以及色散的实现
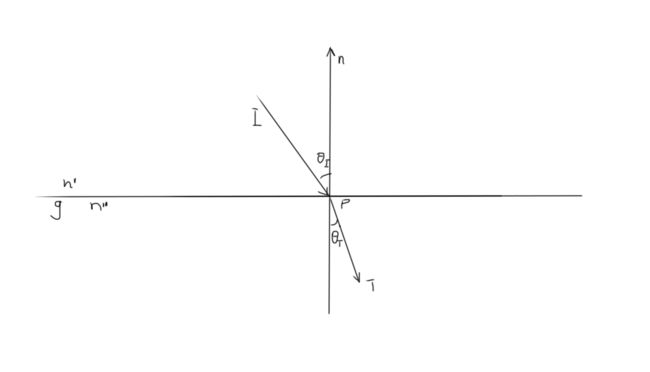
折射可以解释透过玻璃所看到的扭曲的景象。
假设g为玻璃,空气的折射率为n’,玻璃的折射率为n’’
当入射向量接触到介质g后,根据折射率n’与n"的差别,它的前行方向将会发生变化。
这种变化可用斯涅耳定律来进行计算:
snell’s law: n ′ s i n θ i = n ′ ′ s i n θ T n'sin\theta_i=n''sin\theta_T n′sinθi=n′′sinθT
在Shader中,折射的计算也被简化成了一个方法:
T=refract(I,n,etaRatio);
其中etaRatio=n’/n’’。
各种介质的etaRatio一览:
————————————————
真空:1.0
水:1.3333
玻璃:1.5
钻石:2.417
水晶: 1.544-1.553
————————————————
所以空气中的光经过玻璃后的公式就是:
T=refract(I,n,1/1.5);
色散的实现:
最上面解释过,在光学中,复色光通过介质产生折射时,由于复色光中各个光的波长(影响折射率)不同而导致各个光线依次分开。
所以首先看下复色光中各个光的波长:
——————————
红:620-750nm
橙:590nm
黄:570nm
绿:495nm
青:450nm
蓝:420nm
紫:380nm
——————————
由于折射率是取决于波长的,所以折射出的各个颜色的光的顺序总是一致的。
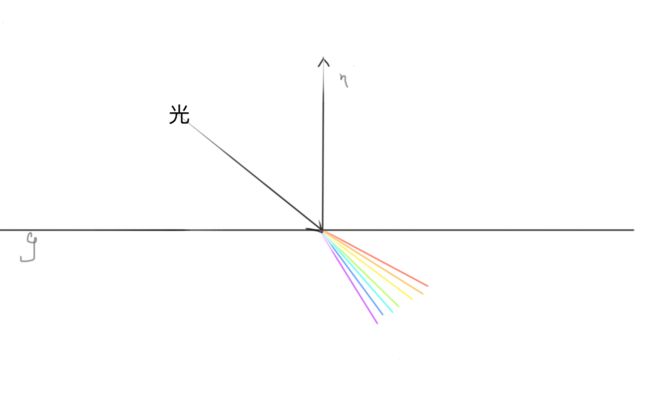
代码,这里假设复色光中只有红绿蓝来做示例:
先将折射率计算好,存在etaRatio的x,y,z中。
float3 Tred=refract(normalize(-worldViewDir),i.normal,etaRatio.x);
float3 Tgreen=refract(normalize(-worldViewDir),i.normal,etaRatio.y);
float3 Tblue=refract(normalize(-worldViewDir),i.normal,etaRatio.z);
算出折射后的向量,分别对天空盒进行立方体采样,并只取相应的红绿蓝颜色分量。
float4 refractedColor;
refractedColor.r=DecodeHDR (UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, Tred),unity_SpecCube0_HDR).r;
refractedColor.g=DecodeHDR (UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, Tgreen),unity_SpecCube0_HDR).g;
refractedColor.b=DecodeHDR (UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, Tblue),unity_SpecCube0_HDR).b;
refractedColor既是视角观察介质后方天空盒时产生的色散效果。
4,菲涅尔效果
定义:
当光从一种具有折射率的介质向另一种具有折射率为的介质传播时,在两者的交界处(通常称作界面)可能会同时发生光的反射和折射。菲涅尔方程描述了不同光波分量被折射和反射的情况。
https://zh.wikipedia.org/wiki/%E8%8F%B2%E6%B6%85%E8%80%B3%E6%96%B9%E7%A8%8B
根据wiki描述,依照菲涅尔方程可以计算出一定功率的入射光被界面反射的比例反射比R和折射的比例透视比T。那么在实时光照的世界中,我对它的理解是,当上文中的反射采样的rbga与折射采样的rgba根据R,T的比例进行混合既能模拟出菲涅尔效果。
在不考虑偏振的情况下,计算折射比T与反射比R的数学公式为:
反射折射比算法1:
R = s i n ( θ t − θ i ) s i n ( θ t + θ i ) R=\frac{sin(\theta_t-\theta_i)}{sin(\theta_t+\theta_i)} R=sin(θt+θi)sin(θt−θi)
T=R-1
下图interface为介质,normal为法线,P为入射向量,S为折射向量,Q为反射向量。
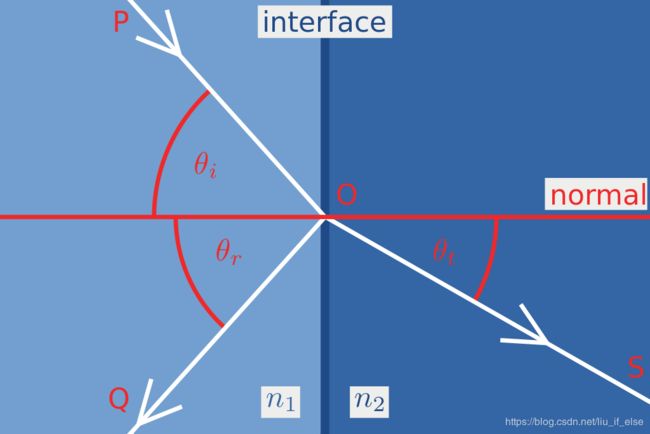
网上还有其他的对一些特定介质的计算公式,有兴趣的可以研究一下,例如这是一篇有关玻璃的反射率和透光率的文章https://wenku.baidu.com/view/1431cbee81c758f5f61f67ec.html。
5,拥有菲涅尔与色散效果的环境映射
综合以上写一个Shader,将计算全部放到了片段着色器中:
//liu_if_else
//modified:2020-2-21
Shader "Unlit/DispersionBeta"
{
Properties {
}
SubShader
{
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
struct v2f {
float3 normal:NORMAL;
float4 pos : SV_POSITION;
float4 objectPOS:float;
};
v2f vert (float4 vertex : POSITION, float3 normal : NORMAL)
{
v2f o;
o.pos = UnityObjectToClipPos(vertex);
o.normal=normal;
o.objectPOS=vertex;
return o;
}
fixed4 frag (v2f i) : SV_Target
{
float dispersionFactor=1.0f; //色散增强,1为不增强
//真空-->玻璃 折射率 1/1.5
//红绿兰折射率:1.6473 ,1.6527 ,1.6726
//红绿兰三色波长相对比率 0.9967/1/1.012
//假设折射以绿光为基准
float3 etaRatio=float3(0.9967f*dispersionFactor,1.0f,1.012f*dispersionFactor)/1.5f;
//基础向量变换
i.normal = UnityObjectToWorldNormal(i.normal);
float3 worldPos = mul(unity_ObjectToWorld, i.objectPOS).xyz;
float3 worldViewDir = UnityWorldSpaceViewDir(worldPos);
i.normal=normalize(i.normal);
//反射向量
float3 reflectVec=reflect(-worldViewDir,i.normal);
//折射向量
float3 refractionVec=normalize(-worldViewDir);
//折射色散向量
float3 tRed=refract(refractionVec,i.normal,etaRatio.x);
float3 tGreen=refract(refractionVec,i.normal,etaRatio.y);
float3 tBlue=refract(refractionVec,i.normal,etaRatio.z);
//反射向量采样天空盒
half4 skyData = UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, reflectVec);
float4 reflectedColor=float4(DecodeHDR (skyData, unity_SpecCube0_HDR),1.0f);
//折射向量采样天空盒
float4 refractedColor=1.0f;
refractedColor.r=DecodeHDR (UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, tRed),unity_SpecCube0_HDR).r;
refractedColor.g=DecodeHDR (UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, tGreen),unity_SpecCube0_HDR).g;
refractedColor.b=DecodeHDR (UNITY_SAMPLE_TEXCUBE(unity_SpecCube0, tBlue),unity_SpecCube0_HDR).b;
/*
//动态计算菲涅尔方程计算折射比与反射比
//先求入射向量与法线夹角
worldViewDir=normalize(worldViewDir);
float theta_i = acos(dot(i.normal.xyz,worldViewDir.xyz));
float theta_t = acos(dot(-i.normal.xyz,normalize(tBlue)));
//反射比R
float ratio_r=pow(sin(radians(-16.88f))/sin(radians(73.1252f)),2.0f);
ratio_r=(ratio_r+pow(tan(theta_t-theta_i)/tan(theta_t+theta_i),2.0f))/2.0f;
float ratio_r=(sin(theta_t-theta_i)/sin(theta_t+theta_i))*(sin(theta_t-theta_i)/sin(theta_t+theta_i));
//折射比T
float ratio_t=1.0f-ratio_r;
*/
//以上反射效果不好,改为以下固定值
//对于普通的玻璃,反射比大约为4% https://wenku.baidu.com/view/1431cbee81c758f5f61f67ec.html
float ratio_r=0.04f;//0.04f;
float ratio_t=0.83f;//1.0;//0.83f;
//反射颜色与折射颜色按比例混合
fixed4 finalColor=refractedColor*ratio_t+reflectedColor*ratio_r;
return finalColor;
}
ENDCG
}
}
}

(折射率0.83,反射率0.04)

(折射率0.6,反射率0.4)

(折射率0.83,反射率0.04,色散增强1.025)
——————————————————————————————————
参考资料:
Cg Tutorial–Nvidia
维基百科
https://en.wikipedia.org/wiki/Chromatic_aberration
https://zh.wikipedia.org/wiki/%E8%8F%B2%E6%B6%85%E8%80%B3%E6%96%B9%E7%A8%8B
百度百科
http://baike.baidu.com/link?url=mfGv-8-d_GLdSBfpzsxV38M9ugwIxgbTlEe6neAQziOMVLuJ27_ZM7y0TKNYMbiknrE9aN8qW2ZTGD0pMRJ1bkyYEP_z_u2cNu3kbulXMQu
————————————————————————————————
维护日志:
2017-8-22:修改了标题
2020-2-8:review,修改了菲涅尔方程部分,更改shader和效果图