进阶python数据分析,python科学计算包numpy[从入门到精通]
Numpy是python最基本最常用的科学计算库,在数据分析,机器学习,深度学习等领域经常被使用,可以说是学习python必学的一个库。我们现在按照数组的创建、数组的存载、数组的获取、数组的变形、和数组的计算等内容来学习 NumPy
本文就数组创建、数组存载和数组获取、数组变形、数组计算进行了学习。
numpy的导入:
import numpy as np
(一)数组的创建
有三种方式:
按步就班的 np.array() 用在列表和元组上
定隔定点的 np.arange() 和 np.linspace()
一步就位的 np.ones(), np.zeros(), np.eye() 和 np.random.random()
按步就班法
import numpy as np
arr = [1,2,3,4,5]
tup=(2,4,6,8,10)
print(np.array(arr))
print(np.array(tup))
#输出结果:
[1 2 3 4 5]
[ 2 4 6 8 10]
定隔定点法
更常见的两种创建 numpy 数组方法:定隔的 arange:固定元素大小间隔,定点的 linspace:固定元素个数
import numpy as np
print( np.arange(8) )
print( np.arange(2,8) )
print( np.arange(2,8,2))
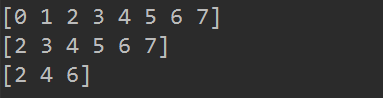
函数 arange用法: arange(start , stop , step)
其中 stop 必须要有,start 没有的话默认为 1,step 没有的话默认为 1。对着这个规则看看上面各种情况的输出。
在看linspace的例子:
import numpy as np
print( np.linspace(1,10,5) )
print( np.linspace(2,20,3) )

函数 linspace用法: linspace (start , stop , num)
其中 start 和 stop 必须要有,num 没有的话默认为 50。对着这个规则看看上面各种情况的输出。
一步到位法
NumPy一次性创建数组
(1)用 zeros() 创建全是 0 的 n 维数组
(2)用 ones() 创建全是 1 的 n 维数组
(3)用 random() 创建随机 n 维数组
(4)用 eye() 创建对角矩阵 (二维数组)
前三种输出是 n 维数组,它们的参数是一个「标量」或「元组类型的形状」
import numpy as np
print( np.zeros(10) ) # 标量5代表形状(5,)
print( np.ones((2,8)) )
print( np.random.random((2,4,4)) )
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第1张图片](http://img.e-com-net.com/image/info8/f2e8964b55d4494cadaa5f2cb4057dbc.jpg)
函数 eye()的参数就是一个标量,控制矩阵的行数或列数;此外还可以设定 eye() 里面的参数 k,默认设置 k = 0 代表 1 落在对角线上
k = 1 代表 1 落在对角线右上方
k = -1 代表 1 落在对角线左下方
import numpy as np
print(np.eye(4))
print(np.eye(4,k=1))
print(np.eye(4,k=-1))
现在我们会用 dir(arr) 来查看数组的属性了:
import numpy as np
arr=np.arange(8)
print(dir(arr))
看完之后我们对 type, ndim, len, size, shape, stride, dtype 几个感兴趣,打印出来看看吧!
import numpy as np
arr=np.arange(8)
print( 'The type is', type(arr) )
print( 'The dimension is', arr.ndim )
print( 'The length of array is', len(arr) )
print( 'The number of elements is', arr.size )
print( 'The shape of array is', arr.shape )
print( 'The stride of array is', arr.strides )
print( 'The type of elements is', arr.dtype )
数组的存载
数组的「保存」和「加载」很重要。假设你已经训练完一个深度神经网络,该网络就是用无数参数来表示的。比如权重都是 numpy 数组,为了下次不用训练而重复使用,将其保存成 .npy 格式或者 .csv 格式是非常重要的。
用 np.save 函数将 numpy 数组保存为 .npy 格式,具体写法如下:
*np.save( ‘’文件路径名”,数组名)
arr2 = np.array([1,2,3,4,5])
np.save("C:/Users/Administrator/Desktop/python_coding/arr2", arr2)
arr2.npy 保存在C:\Users\Administrator\Desktop\python_coding 所在的根目录下。要加加载它也很简单,用 np.load( “文件路径名” ) 即可:
np.load("C:/Users/Administrator/Desktop/python_coding/arr2")
用 np.savetxt 函数将 numpy 数组保存为 .txt 格式,具体写法如下:
np.savetxt( ‘’文件路径名”,数组 )
arr3= np.array([[1., 2., 3.], [4., 5., 6.]])
np.savetxt(r"C:\Users\Administrator\Desktop\python_coding\arr3", arr3)
用 np.loadtxt( “文件名” ) 即可加载该文件
np.loadtxt(r"C:\Users\Administrator\Desktop\python_coding\arr3")
csv文件
如果我们已经在 arr_from_csv 的 csv 文件里写进去了 [[2,4,6], [3,5,7]],每行的元素是由「分号 ;」来分隔的,展示如下:
用 np.genfromtxt( “文件名” ) 即可加载该文件
np.genfromtxt("arr.csv")
奇怪的是数组里面都是 nan,原因是没有设定好「分隔符 ;」
再用 np.genfromtxt( “文件名”,分隔符 ) 即可加载该文件
np.genfromtxt("arr.csv", delimiter=";")
数组的获取:
获取数组是通过索引 (indexing) 和切片 (slicing) 来完成的,
切片是获取一段特定位置的元素,索引是获取一个特定位置的元素
索引和切片的方式和列表一模一样
切片写法是 arr[start : stop : step]
索引写法是 arr[index]
import numpy as np
arr=np.arange(8)
print(arr[1:6:2])
print(arr[4])

虽然切片操作可以由多次索引操作替代,但两者最大的区别在于:
切片得到的是原数组的一个视图 (view) ,修改切片中的内容会改变原数组
索引得到的是原数组的一个复制 (copy),修改索引中的内容不会改变原数组
import numpy as np
arr=np.arange(10)
a=arr[5]
a=1000
print(arr)
b=arr[5:8]
b[1]=12
print(arr)
import numpy as np
arr=np.array([[1,2,3],[4,5,6],[7,8,9]])
print(arr[2])#获取第三行数据
print(arr[1][0])#获取第二行第一个数据
import numpy as np
arr=np.array([[1,2,3],[4,5,6],[7,8,9]])
print(arr[:2])#获取前两行数据
print(arr[:[:2]])#获取所有行第一个和第三个数据
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第4张图片](http://img.e-com-net.com/image/info8/c203211cddc24ca3bd6d5064d3c2edeb.png)
布尔索引:就是用一个由布尔 (boolean) 类型值组成的数组来选择元素的方法。
假设我们有百度(BAIDU),亚马逊 (AMAZON) 和谷歌 (GOOGLE) 的股票代码 code 数组
股票价格 price 数组:每行记录一天开盘,最高和收盘价格。
import numpy as np
code = np.array(['BAIDU', 'AMAZON', 'GOOGLE', 'BAIDU', 'GOOGLE', 'AMAZON'])
price = np.array([[170,177,169],[150,159,153],
[24,27,26],[165,170,167],
[22,23,20],[155,116,157]])
print(price)
print(price[ code == 'BAIDU' ])#该索引可以获取 BAIDU 的股价
print(price[ code == 'BAIDU', 1: ])#用该索引还可以获取 BAIDU 的最高和收盘价格
print( price[ (code == 'BAIDU')|(code == 'GOOGLE') ])#再试试获取BAIDU和GOOGLE 的股价
print(price[ price < 25 ] = 0)#把股价小于 25 的清零
花式索引是获取数组中想要的特定元素的有效方法
import numpy as np
arr=np.arange(36).reshape(6,6)
print(arr)
print(arr[3,4,5])
print(arr[ [-4,-3,-6] ])#按特定顺序来获取倒数第 4, 3 和 6 行
print(arr[ [1,5,7,2], [0,3,1,2] ])
数组的变形
四大类数组层面上的操作,具体有:
(1)重塑 (reshape) 和打平 (ravel, flatten)
(2)合并 (concatenate, stack) 和分裂 (split)
(3)重复 (repeat) 和拼接 (tile)
(4)其他操作 (sort, insert, delete, copy)
重塑reshape
import numpy as np
arr = np.arange(9)
print( arr )
print( arr.reshape((3,3)) )
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第9张图片](http://img.e-com-net.com/image/info8/6bd3c00714524849aa01b05e8f93a296.jpg)
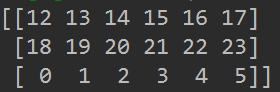
重塑高维矩阵时不想花时间算某一维度的元素个数时,可以用「-1」取代这个维度,程序会自动帮你计算出来。比如把 12 个元素重塑成 (2, 6),你可以写成 (2,-1) 或者 (-1, 6)。
import numpy as np
arr = np.arange(12)
print( arr.reshape((2,-1)) )
print( arr.reshape((-1,6)) )
打平:
用 ravel() 或flatten() 函数将二维数组 arr 打平成一维数组。
arr = np.arange(8).reshape((4,2))
print( arr )
arr1 = arr.ravel()
print( arr1)
arr2 = arr.flatten()
print( arr2)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第11张图片](http://img.e-com-net.com/image/info8/7614de56559e472ca09bec82dba95e7e.png)
通过打平后的数组可以发现,在 numpy 数组中,默认的是行主序
如果你想在ravel和flatten时用列主序,只用把 order 设为 ‘F’,以重塑举例:
import numpy as np
arr = np.arange(8).reshape((4,2),order='F')
arr1 = arr.ravel()
print(arr1)
arr2 = arr.flatten()
print(arr2)

函数 ravel() 或 flatten() 的不同之处是:ravel() 按「行主序」打平时没有复制原数组,因此改变其中的元素数组会改变,按「列主序」在打平时复制了原数组;flatten() 在打平时复制了原数组,它们中元素的改变都不会引起数组的改变。
import numpy as np
arr = np.arange(6).reshape(2,3)
print( arr )
flatten_arr = arr.flatten()
print( flatten_arr )
flatten_arr[0] = 10000
print( arr )
import numpy as np
arr = np.arange(6).reshape(2,3)
print( arr )
ravel_arr = arr.ravel( order='F' )
ravel_arr[0] = 10000
print( ravel_F )
print( arr )
import numpy as np
arr = np.arange(6).reshape(2,3)
print( arr )
new_arr=arr.ravel()
new_arr[4]=1000
print(arr)
合并与分裂数组
合并 (concatenate, stack) 和分裂 (split) 这两个操作仅仅只改变数组的分合:合并是多合一,分裂是一分多
**「合并」**函数有三种:
(1)通用的 concatenate
(2)专门的 vstack, hstack, dstack
(3)极简的 r_, c_
concatenate() 函数:通过axis=0或者1设定轴,来对数组进行竖直方向合并 (axis=0) 和水平方向合并 (axis=1)。
import numpy as np
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[11, 12, 13], [14, 15, 16]])
print(np.concatenate([arr1,arr2],axis=0))
print(np.concatenate([arr1,arr2],axis=1))
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第15张图片](http://img.e-com-net.com/image/info8/bee3986ffa6e4ce399651633ee7684d8.jpg)
NumPy 里还有专门合并的函数
vstack:v 代表 vertical,竖直合并,等价于 concatenate(axis=0)
hstack:h 代表 horizontal,水平合并,等价于 concatenate(axis=1)
dstack:d 代表 depth-wise,按深度合并,深度有点像彩色照片的 RGB 通道,和 vstack, hstack 不同,dstack 将原数组的维度增加了一维。
import numpy as np
arr1=np.array([[1,2,3,4],[5,6,7,8]])
arr2=np.array([[11,12,13,14],[15,16,17,18]])
print(np.vstack((arr1,arr2)))
print(np.hstack((arr1,arr2)))
print(np.dstack((arr1,arr2)))
print(np.dstack((arr1,arr2)).shape)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第16张图片](http://img.e-com-net.com/image/info8/6ad785063c6649eea5db638ec7c6813f.jpg) 还有一种更简单的在竖直和水平方向合并的函数,r_() 和 c_()。
还有一种更简单的在竖直和水平方向合并的函数,r_() 和 c_()。
import numpy as np
arr1 = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
arr2 = np.array([[11, 12, 13, 14], [15, 16, 17, 18]])
print(np.r_[arr1, arr2])
print(np.c_[arr1, arr2])
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第17张图片](http://img.e-com-net.com/image/info8/b0158807e1b44b1388124dc68b586b98.jpg) 再来看看他们的其他用法:1. 参数可以是切片。2. 第一个参数可以是控制参数,如果它用 ‘r’ 或 ‘c’ 字符可生成线性代数最常用的 matrix (和二维 numpy array 稍微有些不同)3. 第一个参数可以是控制参数,如果它写成 ‘a,b,c’ 的形式,其中,a:代表轴,按「轴 a」来合并,b:合并后数组维度至少是 b,c:在第 c 维上做维度提升。
再来看看他们的其他用法:1. 参数可以是切片。2. 第一个参数可以是控制参数,如果它用 ‘r’ 或 ‘c’ 字符可生成线性代数最常用的 matrix (和二维 numpy array 稍微有些不同)3. 第一个参数可以是控制参数,如果它写成 ‘a,b,c’ 的形式,其中,a:代表轴,按「轴 a」来合并,b:合并后数组维度至少是 b,c:在第 c 维上做维度提升。
import numpy as np
print( np.r_[-2:2:1, [0]*3, 5, 6] )
print(np.r_['r', [1,2,3], [4,5,6]])
print( np.r_['0,2,0', [1,2,3], [4,5,6]] )
print( np.r_['0,2,1', [1,2,3], [4,5,6]] )
print( np.r_['1,2,0', [1,2,3], [4,5,6]] )
print( np.r_['1,2,1', [1,2,3], [4,5,6]] )
分裂:「分裂」函数有两种选择“”
(1)有通用的 split
(2)有专门的 hsplit, vsplit
split:和 concatenate() 函数一样,我们可以在 split() 函数里通过设定轴,来对数组沿着竖直方向分裂 (轴 0) 和沿着水平方向分裂 (轴 1)。
import numpy as np
arr=np.arange(36).reshape((6,6))
first, second, third = np.split(arr,[1,3])
print( 'The first split is', first )
print( 'The second split is', second )
print( 'The third split is', third )
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第19张图片](http://img.e-com-net.com/image/info8/07ce26adc3fd498e8b00c5ede7b42b4f.png)
split() 默认沿着纵向分裂,其第二个参数 [1, 3] 相当于是个切片操作,将数组分成三部分:
第一部分 :1 (即第 1 行)
第二部分: 1:3 (即第 2 到 3 行)
第二部分: 3: (即第 4 到 5 行)
hsplit:
import numpy as np
arr=np.arange(36).reshape((6,6))
first, second, third = np.hsplit(arr,[1,3])
print( 'The first split is', first )
print( 'The second split is', second )
print( 'The third split is', third )
重复 (repeat) 和拼接 (tile) :
重复是在元素层面复制
拼接是在数组层面复制
import numpy as np
arr=np.arange(5)
new_arr=arr.repeat(2)
print(new_arr) #数组 arr 中每个元素复制2遍
print(arr.repeat([0,1,2,3,4])) # 数组 arr 中每个元素分别复制0,1 2, 3, 4 遍。
import numpy as np
arr2 = np.arange(10).reshape((2,-1))
print( arr2 )
print( arr2.repeat(2, axis=0) )
print( arr2.repeat([0,1,2,3,4], axis=1) )
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第22张图片](http://img.e-com-net.com/image/info8/306f2f8d3eeb47c1821769ba9c001446.jpg)
tile() 复制的是数组本身,参数有几种设定方法:
(1)标量:把数组当成一个元素,一列一列复制
(2)形状:把数组当成一个元素,按形状复制
import numpy as np
arr=np.arange(9).reshape((3,3))
print(arr.tile(2)) #数组 arr 按列复制 2 遍。
print(arr.tile(2,3)) #数组 arr 按形状复制 6 (2×3) 遍,并以 (2,3) 的形式展现。
数组的排序 (sort),插入 (insert),删除 (delete) 和复制 (copy)。
排序sort:用来排序 numpy 用两种方式:
arr.sort()
np.sort( arr )
第一种 sort 会改变 arr,第二种 sort 在排序时创建了 arr 的一个复制品,不会改变 arr。
import numpy as np
arr = np.array([5,3,2,6,1,4])
print(arr)
arr.sort()
print(arr)
print(arr[::-1])
import numpy as np
arr=np.random.randint(30,size=(3,4))
print(arr)
arr[1,:].sort()
print(arr)
import numpy as np
arr=np.random.randint(40,size=(3,4))
print(arr)
print(np.sort(arr[1,:]))
print(arr)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第26张图片](http://img.e-com-net.com/image/info8/b9c71737e87642f3b6cfaed2fcf910b0.jpg) 有时候我们不仅仅只想排序数组,还想在排序过程中提取每个元素在原数组对应的索引(index),这时 argsort() 就派上用场了。
有时候我们不仅仅只想排序数组,还想在排序过程中提取每个元素在原数组对应的索引(index),这时 argsort() 就派上用场了。
import numpy as np
arr = np.array([100, 80, 99, 87, 91])
idx = arr.argsort()
print( idx )
![]() 这个 idx = [1 3 4 2 0] 怎么理解呢?很简单,排序完之后分数应该是 [80 87 91 99 100],
这个 idx = [1 3 4 2 0] 怎么理解呢?很简单,排序完之后分数应该是 [80 87 91 99 100],
80,即 score[1] 排在第0位, 因此 idx[0] =1
87,即 score[3] 排在第1 位, 因此 idx[1] =3
91,即 score[4] 排在第2 位, 因此 idx[2] =4
99,即 score[2] 排在第3 位, 因此 idx[3] =2
100,即 score[0] 排在第4 位, 因此 idx[4] =0
插入和删除
和列表一样,我们可以给 numpy 数组
用insert()函数在某个特定位置之前插入元素
用delete()函数删除某些特定元素
import numpy as np
arr = np.arange(8)
print( arr )
print( np.insert(arr, 1, 100) )
print( np.delete(arr, [1,3]) )
复制
用copy()函数来复制数组 arr 得到 arr_copy,改变 arr_copy 里面的元素不会改变 arr。
import numpy as np
arr = np.arange(8)
arr_copy = arr.copy()
print(arr )
print(arr_copy )
arr_copy[-1] = 99
print(arr_copy )
print( arr )
数组的计算
四大类数组计算,具体有
(1)元素层面 (element-wise) 计算
(2)线性代数 (linear algebra) 计算
(3)元素整合 (element aggregation) 计算
(4)广播机制 (broadcasting) 计算
元素层面计算
Numpy 数组元素层面计算包括:
(1)二元运算 (binary operation):加减乘除
(2)数学函数:倒数、平方、指数、对数
(3)比较运算 (comparison)
(1)加减乘除运算:
import numpy as np
arr1 = np.array([[1., 2., 3.], [4., 5., 6.]])
arr2 = np.array([[11,12,13],[14,15,16]])
print( arr1 )
print( arr2 )
print( arr1 + arr2)
print( arr1 - arr2 )
print( arr1 * arr2 )
print( arr1 / arr2 )
import numpy as np
arr = np.array([[1., 2., 3.], [4., 5., 6.]])
print( 1 / arr )
print( arr ** 2 )
print( np.exp(arr) )
print( np.log(arr) )
import numpy as np
arr1 = np.array([[1., 2., 3.], [4., 5., 6.]])
arr2 = np.array([[11,12,13],[14,15,16]])
print( arr1>arr2 )
print(arr1>3)
线性代数计算
创建数组 arr1 和矩阵 A并且查看他们的转置,注意输出有 array 和 matrix 的关键词。
import numpy as np
arr1 = np.array([[1,2],[3,1]])
A = np.asmatrix(arr1)
print(arr1)
print(A)
print( arr1.T )
print( arr1.transpose() )
print( A.T )
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第31张图片](http://img.e-com-net.com/image/info8/4640415f3f244440bf58db24f99de68a.jpg) 求逆:数组用 np.linalg.inv() 函数,而矩阵用 A.I 和 A**-1 操作。
求逆:数组用 np.linalg.inv() 函数,而矩阵用 A.I 和 A**-1 操作。
import numpy as np
arr1 = np.array([[1,2],[3,1]])
A = np.asmatrix(arr1)
print( np.linalg.inv(arr1) )
print( A.I )
print( A**-1 )
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第32张图片](http://img.e-com-net.com/image/info8/7f47a47bbd5a42cba916495e33c3eb65.png) **相乘:**数组相乘是在元素层面进行,
**相乘:**数组相乘是在元素层面进行,
矩阵相乘要就是数学定义的矩阵相乘 (比如第一个矩阵的列要和第二个矩阵的行一样)
import numpy as np
arr1 = np.array([[1,2],[3,1]])
A = np.asmatrix(arr1)
arr = np.array([1,2])
b = np.asmatrix(arr).T
print( arr1*arr )
print( A*b )
import numpy as np
arr1 = np.array([[1,2],[3,1]])
A = np.asmatrix(arr1)
print(arr1*arr1)
print(A*A)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第34张图片](http://img.e-com-net.com/image/info8/6219b6c398c74c58ab2a3a316413d8dc.png)
虽然两个二维数组相乘得到二维数组,其结果由元素层面相乘得到的。两个 [[1 2], [3,1]] 的元素相乘确实等于 [[1 4], [9,1]]。
而矩阵相乘矩阵的结果和我们学了很多年的线代结果很吻合。
那么怎么才能在数组上实现「矩阵相乘向量」和「矩阵相乘矩阵」呢?
点乘函数 dot()。
(一)np.dot(向量, 向量) 实际上做的就是内积,即把两个向量每个元素相乘,最后再加总。
import numpy as np
x = np.array([1, 2, 3])
y = np.array([4, 5, 6])
z = np.dot(x, y)
print(z.shape)
print(z)

(二)np.dot(矩阵, 向量) 实际上做的就是普通的矩阵乘以向量。点乘结果是个向量 (1D 数组),形状 = (2, )。
import numpy as np
x = np.array([1, 2, 3])
y = np.array([[1,2,3], [4,5,6]])
z = np.dot(y, x)
print(z.shape)
print(z)

(三)np.dot(矩阵, 矩阵) 实际上做的就是普通的矩阵乘以矩阵。点乘结果是个矩阵 (2D 数组),形状 = (2, 3)。
import numpy as np
x = np.array( [[1, 2, 3], [1, 2, 3], [1, 2, 3]] )
y = np.array( [[1, 2, 3], [4, 5, 6]] )
z = np.dot(y,x)
print( z.shape )
print( z )
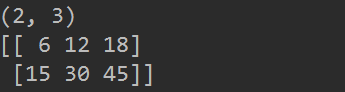
(四)当 x 是 3D 数组,y 是 1D 数组,np.dot(x, y) 是将 x 和 y 最后一维的元素相乘并加总。此例 x 的形状是 (2, 2, 4),y 的形状是 (4, ),因此点乘结果的形状是 (2, 2)。
import numpy as np
x = np.ones(shape=(2, 2, 4))
y = np.array([1, 2, 3, 4])
z = np.dot(x, y)
print(z.shape)
print(z)
 (五)当 x 是 3D 数组,y 是 2D 数组,np.dot(x, y) 是将 x 的最后一维和 y 的倒数第二维的元素相乘并加总。此例 x 的形状是 (3, 3, 4),y 的形状是 (4,3),因此点乘结果的形状是 (3, 3, 4)。
(五)当 x 是 3D 数组,y 是 2D 数组,np.dot(x, y) 是将 x 的最后一维和 y 的倒数第二维的元素相乘并加总。此例 x 的形状是 (3, 3, 4),y 的形状是 (4,3),因此点乘结果的形状是 (3, 3, 4)。
import numpy as np
x = np.random.normal( 0, 1, size=(3, 3, 4) )
y = np.random.normal( 0, 1, size=(4, 3) )
z = np.dot(x,y)
print( z.shape )
print( z )
元素整合
在数组中,元素可以以不同方式整合 (aggregation)。拿求和 (sum) 函数来说,我们可以对数组
所有的元素求和
在某个轴 (axis) 上的元素求和
import numpy as np
arr1 = np.arange(1,7).reshape((2,3))
arr2 = np.arange(1,13).reshape((2,2,3))
print( 'The total sum is', arr1.sum() )
print( 'The sum across rows is', arr1.sum(axis=0) )
print( 'The sum across columns is', arr1.sum(axis=1) )
print( 'The total sum is', arr2.sum() )
print( 'The sum on axis0 is', arr2.sum(axis=0) )
print( 'The sum on axis1 is', arr2.sum(axis=1) )
print( 'The sum on axis2 is', arr2.sum(axis=2) )
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第36张图片](http://img.e-com-net.com/image/info8/31de30b8fc364e909729d0f1cb889c5a.jpg) 除了 sum 函数,整合函数还包括 min, max, mean, std 和 cumsum,分别是求最小值、最大值、均值、标准差和累加,这些函数对数组里的元素整合方式和 sum 函数相同,就不多讲了。总结来说我们可以对数组
除了 sum 函数,整合函数还包括 min, max, mean, std 和 cumsum,分别是求最小值、最大值、均值、标准差和累加,这些函数对数组里的元素整合方式和 sum 函数相同,就不多讲了。总结来说我们可以对数组
所有的元素整合
在某个轴 (axis) 上的元素整合
整合函数= {sum, min, max, mean, std, cumsum}
广播机制:
广播轴 (broadcast axis):比对两个数组的维度,将形状小的数组的维度 (轴) 补齐
复制元素:顺着补齐的轴,将形状小的数组里的元素复制,使得最终形状和另一个数组吻合
总结
本文就数组创建、数组存载和数组获取、数组变形、数组计算进行了学习。
数组变形有以下重要操作:
改变维度的重塑(reshape)和打平(flatten,ravel)
改变分合的合并(stack、concatenate)和分裂(split)
复制本质的重复(repeat)和拼接(tite)
其他排序插入(insert)删除(delete)复制(copy)
数组计算有以下重要操作:
元素层面:四则运算、函数,比较
线性代数:务必弄懂点乘函数 dot()
元素整合:务必弄懂轴axis这个概念!
广播机制:很重要,神经网络无处不在!
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第2张图片](http://img.e-com-net.com/image/info8/27a9cad83c5847e0a609115fdfd59fa2.png)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第3张图片](http://img.e-com-net.com/image/info8/aee2b8f105ce41ce862fb4e86ef028e8.jpg)


![进阶python数据分析,python科学计算包numpy[从入门到精通]_第5张图片](http://img.e-com-net.com/image/info8/262561072a7940b5832864724c46b4a6.png)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第6张图片](http://img.e-com-net.com/image/info8/8fae08db654a44d3861007584aa5eea2.jpg)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第7张图片](http://img.e-com-net.com/image/info8/9cb4ea3b74514987b134a8663308ef95.png)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第8张图片](http://img.e-com-net.com/image/info8/66471b91e80c4670a599eab68c2f3d0c.jpg)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第10张图片](http://img.e-com-net.com/image/info8/e92ebe97370f405f9c13171dbb4c35ea.png)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第12张图片](http://img.e-com-net.com/image/info8/d3b660bd35e34c9e8d9d965aa226b149.png)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第13张图片](http://img.e-com-net.com/image/info8/5a17766ca4ec4c6d8f972dab435fcb1d.png)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第14张图片](http://img.e-com-net.com/image/info8/b3409f86a69344bc9624e485b76cd149.png)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第18张图片](http://img.e-com-net.com/image/info8/a561089b4ddc48d2ac04e71bb22bf97e.jpg)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第20张图片](http://img.e-com-net.com/image/info8/8845a6f3cc6c484a8a45a09257009b48.jpg)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第21张图片](http://img.e-com-net.com/image/info8/629bbd14f105493c8e6c56a23c7a6d88.png)

![进阶python数据分析,python科学计算包numpy[从入门到精通]_第23张图片](http://img.e-com-net.com/image/info8/436a40b26d1843efa2f408d82c4e3f91.jpg)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第24张图片](http://img.e-com-net.com/image/info8/dbee9d59b50e4118acdf0898665d0a48.png)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第25张图片](http://img.e-com-net.com/image/info8/b18464d6a5284a8da9e6686b6589e285.png)

![进阶python数据分析,python科学计算包numpy[从入门到精通]_第27张图片](http://img.e-com-net.com/image/info8/a76090e2ca7f47d29e512aa9ae38282f.png)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第28张图片](http://img.e-com-net.com/image/info8/c824d8c4a33d403a815a33a30b3a528d.jpg)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第29张图片](http://img.e-com-net.com/image/info8/ed49070a317b4677a4d0c04574f334b5.jpg)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第30张图片](http://img.e-com-net.com/image/info8/127b8e1003f94538bd91014bc9e486c1.png)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第33张图片](http://img.e-com-net.com/image/info8/dc08416824b94ab19c625d042d4ea0fb.png)
![进阶python数据分析,python科学计算包numpy[从入门到精通]_第35张图片](http://img.e-com-net.com/image/info8/aae616e062914d609c69d7faa5a8d4db.jpg)