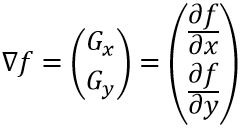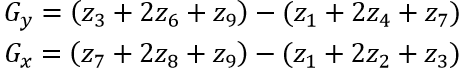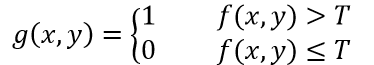图像的阈值分割(Optimum Thresholding)

摘    要：本实验主要实现最优阈值。图像分割就是把图像中具有特殊涵义的不同区域分开来，这些区域是互不相交的，每个区域都满足特定区域的一致性。图像分割是图像处理中的重要问题，也是计算机视觉研究中的一个经典难题。计算机视觉中的图像理解包括目标检测、特征提取和目标识别等，都依赖于分割的质量。阈值法是一种简单有效的分割方法，其最大特点就是计算简单，因此也得到了广泛的应用。

一、技术论证

1.用一阶导数进行图像边缘检测

       在任何关于分割的讨论中，点和线检测都是很重要的，但是边缘检测对于灰度级间断的检测是最为普遍的检测方法。在本实验中我们讨论实现一阶导数检测一幅图像中边缘的方法。首先了解一下数字化边缘的概念：直观上，一条边缘是一组相连的像素集合。这些像素位于两个区域的边界上。

       图1显示了两个区域之间边缘的一条水平的灰度级剖面线。这个图形也显示出灰度级剖面线的一阶导数。当我们沿着剖面线从左到右，在进入和离开斜面的变化点，一阶导数为正。在灰度级不变的区域一阶导数为零。在图1中导数的符号在从亮到暗的跃变边缘处取反。由这些现象我们可以得到的结论是：一阶导数可以用于检测图像中的一个点是否是边缘的点(也就是判断一个点是否在斜坡上)。

图1 图像的灰度函数和其一阶导数

       边缘检测的困难：为了利用边界信息进行分析，所采用的边缘检测方法必须既能检测出强度的不连续性，又要能同时确定它们的精确位置，在图像处理过程中不可避免会遇到噪声干扰。而为了抑制无关的细节和噪声，需要对图像进行某种平滑滤波，但平滑又会导致定位精度的损失。

2 梯度算子

       一幅数字图像的一阶导数是基于各种二维梯度的近似值。图像f(x,y)在位置(x,y)的为下列向量：

           从向量分析中我们知道，梯度向量指向坐标(x,y)的f的最大变化率方向。在边缘检测中，一个重要的量是这个向量的大小，用表示，这里有：

   这个量给出了在方向上每增加单位距离后f(x,y)值增大的最大变化率。一般来讲也将称为梯度(尽管并不完全正确)。

3 Sobel算子

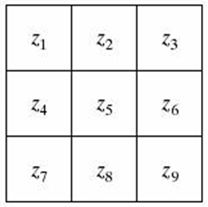
   计算图像的梯度要基于在每个像素位置都得到了偏导数∂f/∂x和∂f/∂y。图2中显示的3×3大小的区域表示图像邻域中的灰度级。若要得到z5点处的一阶偏导数，可以使用Sobel算子。

图2 3×3图像邻域的灰度级

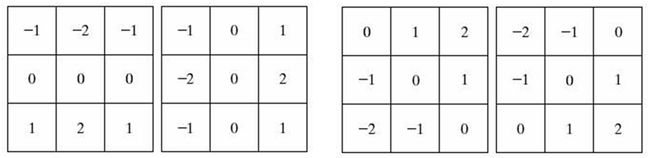
   图3称为Sobel算子，用以实现Gx和Gy这两个公式。Prewitt和Sobel算子是在实践中计算数字梯度时最常用的。Prewitt模板实现起来比Sobel模板更为简单，但后者在噪声抑制特性方面略胜一筹，这在处理导数时是个重要的问题。

    梯度的计算需要Gx和Gy这两个分式联合使用。然而，实际执行中并不总能令人满意。因为计算平方方根需要大量计算。经常使用的一种方法是用绝对值对梯度进行近似：

    这个公式在计算方面更加简便，而且它仍保持着同灰度级的相对变化。而得到这个优点的代价是通常导致滤波器不是各向同性的(对于旋转变换不变)。然而，当用Prewitt和Sobel一类的模板去计算Gx和Gy时这并不构成问题。

图3 四种3×3 Sobel模板

4 图像分割的门限处理

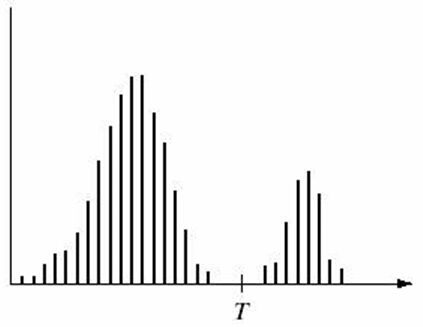
    由于图像门限处理的直观性和易于实现的性质，使它在图像分割应用中处在中心地位。假设图4所示的灰度级直方图对应于一幅图像f(x,y)。这幅图像由亮的对象和深的背景组成，这样的组成方式将对象和背景具有灰度级的像素分成两组不同的支配模式。从背景中提取对象的一种显然的方法是选择一个门限值T，将这些模式分离开。然后，所有f(x,y)>T的点(x,y)称为对象点；否则，就称为背景点。该方法可用以下公式表示：

图4 门限值在灰度直方图中的表示

5 自动估计阈值的全局门限处理

    图5显示了一幅简单的图像，及它的直方图，并使用门限T分割得到结果，门限T是灰度级最大值和最小值的中间值。这个门限去除了阴影部分，只留下对象本身，实现了对图像“干净的”分割。此时，我们关注的对象比背景更暗，所以，任何灰度级小于等于T的像素都被标记为黑色 ，任何灰度级大于T的像素被标记为白色 。关键目的是生成一幅二值图像，以便倒转黑白关系。

图5 图像的阈值分割

下面的算法可以用于自动地得到阈值T：
1．选择一个T的初始估计值。
2．用T分割图像。这样做会生成两组像素：G1由所有灰度值大于T的像素组成，而G2由所有灰度值小于或等于T的像素组成。
3．对区域G1和G2中的所有像素计算平均灰度值μ1和μ2。
4．计算新的门限值：T=(μ1+μ2)/2
5．重复步骤2到4，直到逐次迭代所得的T值之差小于事先定义的参数T0。

二、实验结果讨论

    本实验使用图像均取自冈萨雷斯主编数字图像处理第三版中。图像Fig9.39(a).jpg用于实现Sobel梯度算子和平滑滤波后的边缘检测，使用图像Fig10.36(b).jpg实现自动调整阈值的图像分割。

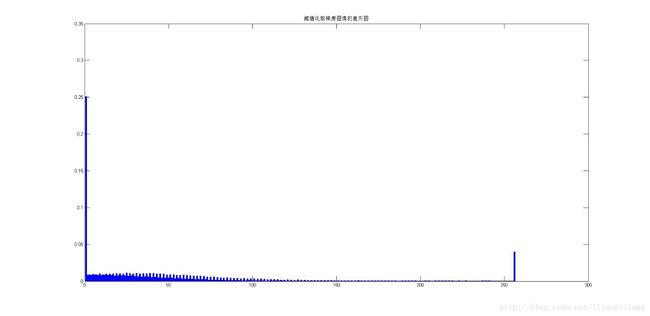
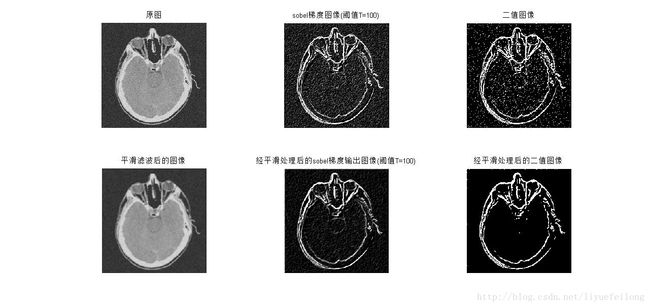
    编写函数[gradient,binary] = sobel(ima,T)实现Sobel算子梯度运算并输出梯度图像和二值图像，其中ima为输入图像，T为阈值。在设定阈值T时需要分析输入图像的直方图,如图6所示，可以观察图像的灰度值主要集中在100以下，在255处也出现了一个峰值，故将阈值设定为100。图7上三个图给出了处理结果，可以看到Sobel算子较好地输出了图像的边缘，但二值图像中有明显的噪声。

    图7下方三个图给出了进行平滑滤波之后的Sobel梯度运算结果。可以看到对滤波后的图像做梯度运算后，噪声基本消失。由此带来的代价是精度的丢失，二值图像的边缘细节没有上第三个图的丰富。

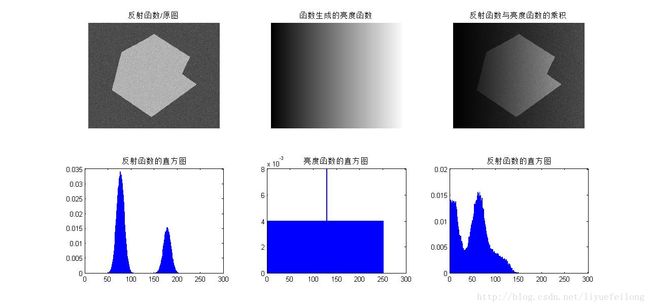
    在进行自动调整阈值的图像分割前，对图像Fig10.36(b).jpg进行光线渐变处理，编写函数out_img = LightGradient(ima)可实现这一处理。其中ima为输入图像，out_img为输出图像。处理前后的图像如图8所示。可以看到进行光线渐变处理后的图像直方图变得紧凑，使得使用阈值T进行图像分割变得困难。

    编写函数[out,T]=GlobalThreshold(ima)实现自动调整阈值的图像分割，ima为输入图像，out为输出图像，T为自动调整后的阈值，图9和图10分别给出自适应的阈值和分割后的二值图像，可以看到分割的效果并不理想，图像有明显的早点，且阈值临界点处的分割无法做到一条平整的直线。

    因此对图像进行平滑滤波后再进行阈值分割，得到图11中的输出结果，其效果大幅改善。如要得到更好的效果，需要对图像进行分块处理，如基于Otus方法的最佳阈值处理。

三、实验结果图片

图6 输入图像Fig9.39(a).jpg的直方图

图7 平滑滤波对Sobel梯度运算的结果影响

图8 对图像进行光线渐变处理及其直方图

图9 自动调整后的阈值T

图10 自适应的阈值分割后的二值图像

图11 经过平滑滤波的自适应的阈值分割后的二值图像

    以下给出MATLAB代码：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 函数名：sobel算子边缘检测
% 输入：输入图像ima，阈值T
% 输出：二值图像binary，边缘检测梯度输出图像gradient
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [gradient,binary] = sobel(ima,T)
sobel_operator1 = [-1,-2,-1;0,0,0;1,2,1];
sobel_operator2 = [-1,0,1;-2,0,2;-1,0,1];
Gx = imfilter(ima,sobel_operator1);   % 进行空域滤波
Gy = imfilter(ima,sobel_operator2);
gradient = abs(Gx)+abs(Gy);        % 用绝对值的和代替梯度
binary = zeros(size(ima));
binary(find(gradient>T))=1;    　   % 大于阈值T的像素点判定为1，否则为０

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 函数名：光线渐变算法LightGradient
% 输入：输入图像ima，阈值
% 输出：光线渐变图像out_img
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function out_img = LightGradient(ima)
ima = imread('Fig10.36(b).jpg');
[x,y] = size(ima);
k = round(y/255);
imt = zeros(x,y);
% 生成一个渐变亮度的函数/图像
for j = 1:y
    imt(:,j) = round(0 + j / k);
end
imt = double(imt)/256;
ima = double(ima)/256;
% 一幅图像可表示为一亮度函数和一反射函数的乘积
for i = 1:x
    for j = 1:y
        out_img(i,j) = imt(i,j) * ima(i,j); 
    end
end
out_img = uint8(out_img*256);
figure,subplot(2,3,1),imshow(ima),title('反射函数/原图');
subplot(2,3,2),imshow(imt),title('函数生成的亮度函数');
subplot(2,3,3),imshow(out_img),title('反射函数与亮度函数的乘积');
% 求输入输出图像的直方图和亮度函数的直方图
hist_ima = imhist(ima) / (x*y);
hist_imt = imhist(imt) / (x*y);
hist_out_img = imhist(out_img) / (x*y);
subplot(2,3,4),bar(1:256,hist_ima,'b'),title('反射函数的直方图');
subplot(2,3,5),bar(1:256,hist_imt,'b'),title('亮度函数的直方图');
subplot(2,3,6),bar(1:256,hist_out_img,'b'),title('反射函数的直方图');

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 函数名：自动调整阈值的图像分割算法GlobalThreshold
% 输入：输入图像ima，阈值
% 输出：光线渐变图像out_img
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [out,T]=GlobalThreshold(ima) 
[x,y] = size(ima);                  
b= double(ima);                    
gray_max = double(max(ima(:)));         % 求输入图像的最大灰度值  
gray_min = double(min(ima(:)));          % 求输入图像的最小灰度值   
T = double((gray_max+gray_min))/2;      % T赋初值，为最大值和最小值的平均值  
count = double(0);                     % 迭代次数 
    while 1                     　　% 阈值迭代 
    sum0 = 0; 　　　　　　　　　% 初始化灰度大于阈值的元素的灰度总值
    num0 = 0;                   % 初始化灰度大于阈值的元素的灰度个数
    sum1 = 0; 　　　　　　　　　% 初始化灰度小于阈值的元素的灰度总值
    num1 = 0;                   % 初始化灰度小于阈值的元素的灰度个数  
    for i=1:x 
        for j=1:y 
            if double(ima(i,j))>=T 
                sum1 = sum1 + double(ima(i,j)); 　 %大于阈域值图像点灰度值累加 
                num1 = num1 + 1;                %大于阈域值图像点个数累加 
            else  
                sum0 = sum0 + double(ima(i,j));  %小于阈域值图像点灰度值累加 
                num0 = num0 + 1;                %小于阀域值图像点个数累加 
            end  
        end  
    end   
    T0 = sum0/num0;                        %求小于阀域的灰度值均值 
    T1 = sum1/num1;                        %求大于阀域的灰度值均值 
    if abs(T-((T0+T1)/2)) < 0.01     %迭代至前后两次阀域值相差小于0.01时停止迭代。 
        break; 
    else 
       T = (T0+T1) / 2;                 % 更新阈值T  
   end  
end  
T1 = round(T)/256;
out = im2bw(ima,T1);               % 图像在最佳阈值下二值化  

%%%%%%%%%%%%%%%%%%%%%主函数%%%%%%%%%%%%%%%%%%%%%%%
ima=imread('Fig9.39(a).jpg');
subplot(2,3,1); 
imshow(ima);
title('原图');
[x,y] = size(ima);

T=100;    % 阈值
[grad_ima,binary_ima]=sobel(ima,T);
subplot(2,3,2);
imshow(grad_ima); 
title('sobel梯度图像(阈值T=100)');
subplot(2,3,3);
imshow(binary_ima); 
title('二值图像');
 
H=[1,1,1;1,1,1;1,1,1]/9;   % 用3×3模板实现平滑滤波
imt=imfilter(ima,H);
subplot(2,3,4); 
imshow(imt); 
title('平滑滤波后的图像');
 
[grad_imt,binary_imt]=sobel(imt,T);
subplot(2,3,5); 
imshow(grad_imt);
title('经平滑处理后的sobel梯度输出图像(阈值T=100)');
subplot(2,3,6); 
imshow(binary_imt); 
title('经平滑处理后的二值图像');

k1 = imhist(grad_ima) / (x * y);
k2 = imhist(grad_imt) / (x * y);
figure;bar(1:256,k1,'b');
title('阈值化前梯度图像的直方图');
% subplot(1,2,2),bar(1:256,k2,'b');

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 第二部分
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
img = imread('Fig10.36(b).jpg');
out_img = LightGradient(img);
[out,T]=GlobalThreshold(out_img);
T = T
figure,subplot(1,2,1),imshow(out_img);title('光线渐变图像');
subplot(1,2,2),imshow(out),title('自动估计阈值的图像分割图像输出');