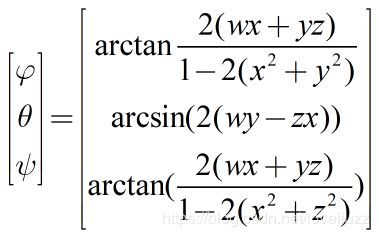头部姿态估计原理及可视化

一、简述

       头部姿态估计（Head Pose Estimation ）：通过一幅面部图像来获得头部的姿态角. 在3D 空间中，表示物体的旋转可以由三个欧拉角(Euler Angle)来表示：分别计算 pitch(围绕X轴旋转)，yaw(围绕Y轴旋转) 和 roll(围绕Z轴旋转) ，分别学名俯仰角、偏航角和滚转角，通俗讲就是抬头、摇头和转头。百闻不如一见，上示意图：

                                      

二、原理

      若对相机标定熟悉的话，就比较好理解，因为 Head Pose Estimation 比较有难度的部分已经被大牛们搞定了，一种比较经典的 Head Pose Estimation 算法的步骤一般为：

（1）2D人脸关键点检测；（2）3D人脸模型匹配；（3）求解3D点和对应2D点的转换关系；（4）根据旋转矩阵求解欧拉角。

众所周知一个物体相对于相机的姿态可以使用旋转矩阵和平移矩阵来表示：

（1）平移矩阵：物体相对于相机的空间位置关系矩阵，用T表示；

（2）旋转矩阵：物体相对于相机的空间姿态关系矩阵，用R表示.

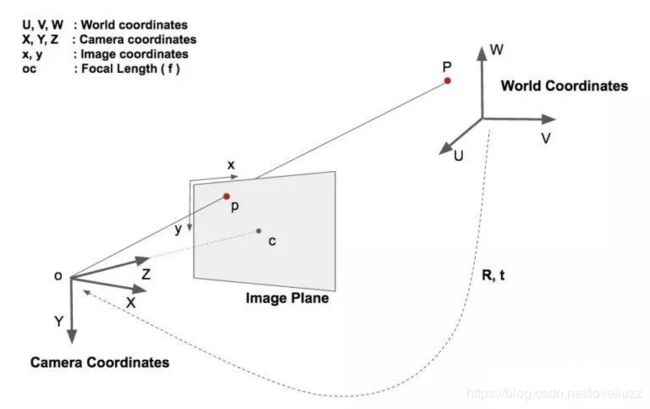
看来必然少不了坐标系转换，分别是：世界坐标系(UVW)、相机坐标系(XYZ)、图像中心坐标系(uv)和像素坐标系(xy)，如下图：

               

世界坐标系到相机坐标系：

                                               

相机坐标系到像素坐标系：

                                                    

像素坐标系和世界坐标系的关系如下：

                                              

         上式的求解可用DLT(Direct Linear Transform)算法结合最小二乘进行迭代求解, 相机总有点瑕疵，比如径向和切向畸变，那关系就要稍微复杂一些，相机坐标系要先转换到图像中心坐标系, 图像中心坐标系到像素坐标系:

                                                    

       确定pose就是：确定从3D model到图片中人脸的仿射变换矩阵，它包含旋转和平移的信息；看来只要知道世界坐标系内点的位置、像素坐标位置和相机参数就可以搞定旋转和平移矩阵，关系分明是非线性的，其实OpenCV已经给我们提供了求解PnP问题的函数solvePnp()，它的输出结果包括旋转向量(roatation vector)和平移向量(translation vector)，只关心旋转信息，所以主要将对 roatation vector进行操作。

        得到旋转矩阵后，就可以得到欧拉角了。rotation vector 是物体旋转信息的表示方式之一，是OpenCV常用的表示方式。除了rotation vector还有欧拉角(Euler angle)、旋转矩阵(Rotation Matrix)、方向余弦矩阵(Direction Cosine Matrix)、四元数(Quaternion) 和 轴-角表示(Axis-Angle)。 因为我需要的是欧拉角，所以这里只介绍将rotation vector 转换为欧拉角的方法。 

       三维空间的任意旋转，都可以用绕三维空间的某个轴旋转过某个角度来表示，即Axis-Angle表示方法。Axis可用一个三维向量(x,y,z)来表示，theta可以用一个角度值来表示，直观来讲，一个四维向量(theta,x,y,z)就可以表示出三维空间任意的旋转。 
注意，这里的三维向量(x,y,z)只是用来表示axis的方向朝向，因此更紧凑的表示方式是用一个单位向量来表示方向axis，而用该三维向量的长度来表示角度值theta。这样以来，可以用一个三维向量(theta*x,theta*y, theta*z)就可以表示出三维空间任意的旋转，前提是其中(x,y,z)是单位向量，这就是旋转向量(Rotation Vector)的表示方式。

      四元数(Quaternion)也是一种常用的旋转表示方式。从四元数转换到欧拉角公式较简单，所以我先将rotation vector转换为四元数。假设(x,y,z)是axis方向的单位向量，theta是绕axis转过的角度，那么四元数可以表示为：

                                            
四元数到欧拉角的转换公式如下： 

                                                 

arctan和arcsin的结果为[-pi/2,pi/2]，不能覆盖所有的欧拉角，因此采用atan2代替arctan：

                                   

三、代码实现

import cv2
import math
import numpy as np


def face_orientation(frame, landmarks):
    size = frame.shape  # (height, width, color_channel)

    image_points = np.array([
                            (landmarks[4], landmarks[5]),     # Nose tip
                            (landmarks[10], landmarks[11]),   # Chin
                            (landmarks[0], landmarks[1]),     # Left eye left corner
                            (landmarks[2], landmarks[3]),     # Right eye right corne
                            (landmarks[6], landmarks[7]),     # Left Mouth corner
                            (landmarks[8], landmarks[9])      # Right mouth corner
                        ], dtype="double")




    model_points = np.array([
                            (0.0, 0.0, 0.0),             # Nose tip
                            (0.0, -330.0, -65.0),        # Chin
                            (-165.0, 170.0, -135.0),     # Left eye left corner
                            (165.0, 170.0, -135.0),      # Right eye right corne
                            (-150.0, -150.0, -125.0),    # Left Mouth corner
                            (150.0, -150.0, -125.0)      # Right mouth corner
                        ])

    # Camera internals

    center = (size[1]/2, size[0]/2)
    focal_length = center[0] / np.tan(60/2 * np.pi / 180)   # 焦距
    camera_matrix = np.array(
                         [[focal_length, 0, center[0]],
                         [0, focal_length, center[1]],
                         [0, 0, 1]], dtype="double"
                         )

    dist_coeffs = np.zeros((4, 1))  # Assuming no lens distortion   （距离系数/假设没有镜头失真）
    # 计算旋转矩阵rotation_vector和平移矩阵translation_vector
    (success, rotation_vector, translation_vector) = cv2.solvePnP(model_points, image_points, camera_matrix, dist_coeffs, flags=cv2.CV_ITERATIVE)


    axis = np.float32([[500, 0, 0],
                          [0, 500, 0],
                          [0, 0, 500]])

    imgpts, jac = cv2.projectPoints(axis, rotation_vector, translation_vector, camera_matrix, dist_coeffs)
    modelpts, jac2 = cv2.projectPoints(model_points, rotation_vector, translation_vector, camera_matrix, dist_coeffs)
    rvec_matrix = cv2.Rodrigues(rotation_vector)[0]

    proj_matrix = np.hstack((rvec_matrix, translation_vector))
    eulerAngles = cv2.decomposeProjectionMatrix(proj_matrix)[6]


    pitch, yaw, roll = [math.radians(_) for _ in eulerAngles]


    pitch = math.degrees(math.asin(math.sin(pitch)))
    roll = -math.degrees(math.asin(math.sin(roll)))
    yaw = math.degrees(math.asin(math.sin(yaw)))

    return imgpts, modelpts, (str(int(roll)), str(int(pitch)), str(int(yaw))), (landmarks[4], landmarks[5])

f = open('/home/jerry/Documents/test/test/landmark.txt','r')
for line in iter(f):
    img_info = line.split(' ')
    img_path = img_info[0]
    frame = cv2.imread(img_path)
    landmarks = map(int, img_info[1:])

    print(img_path)
    imgpts, modelpts, rotate_degree, nose = face_orientation(frame, landmarks)

    cv2.line(frame, nose, tuple(imgpts[1].ravel()), (0, 255, 0), 3)  # GREEN
    cv2.line(frame, nose, tuple(imgpts[0].ravel()), (255, 0, 0), 3)  # BLUE
    cv2.line(frame, nose, tuple(imgpts[2].ravel()), (0, 0, 255), 3)  # RED

    remapping = [2,3,0,4,5,1]
    for index in range(len(landmarks)/2):
        random_color = tuple(np.random.random_integers(0,255,size=3))

        cv2.circle(frame, (landmarks[index*2], landmarks[index*2+1]), 5, random_color, -1)
        cv2.circle(frame,  tuple(modelpts[remapping[index]].ravel().astype(int)), 2, random_color, -1)


#    cv2.putText(frame, rotate_degree[0]+' '+rotate_degree[1]+' '+rotate_degree[2], (10, 30),
#                cv2.FONT_HERSHEY_SIMPLEX, 1, (0, 255, 0),
#                thickness=2, lineType=2)

    for j in xrange(len(rotate_degree)):
                cv2.putText(frame, ('{:05.2f}').format(float(rotate_degree[j])), (10, 30 + (50 * j)), cv2.FONT_HERSHEY_SIMPLEX, 1, (0, 255, 0), thickness=2, lineType=2)

    cv2.imwrite('test2/'+img_path.split('/')[1], frame)

f.close()

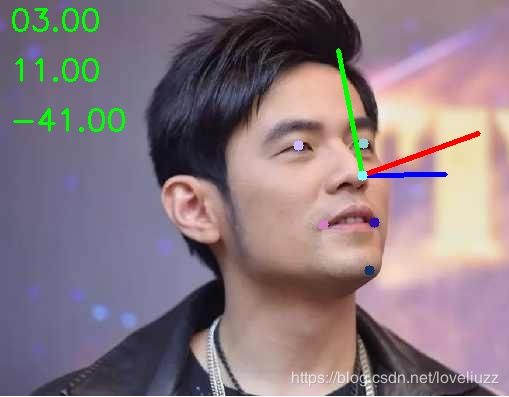
代码运行结果：