深入浅出图神经网络：GNN原理解析（一）

前言

最近在学习图神经网络相关知识，一起来拆书:《深入浅出图神经网络：GNN原理解析》，这本书从原理、算法、实现、应用四个维度详细讲解了图神经网络。接下来打算结合书本内容和相关知识做个专题记录分享，今天先跟大家聊聊关于图的一些基础知识。

为什么要研究图？

在过去的几年中，神经网络的成功推动了模式识别和数据挖掘的研究。许多机器学习任务，如目标检测、机器翻译和语音识别，曾经严重依赖手工的特征工程来提取信息特征集被各种端到端的深度学习范式（例如卷积神经网络（CNN）、长短期记忆（LSTM）和自动编码器）彻底改变了。

尽管深度学习在欧氏空间中的数据方面取得了巨大的成功，但在许多实际的应用场景中的数据是从非欧式空间生成的，同样需要进行有效的分析。图数据的复杂性对现有的机器学习算法提出了重大挑战，这是因为图数据是不规则的。每个图都有一个大小可变的无序节点，图中的每个节点都有不同数量的相邻节点，导致一些重要的操作（例如卷积）在图像上很容易计算，但不再适合直接用于图域。

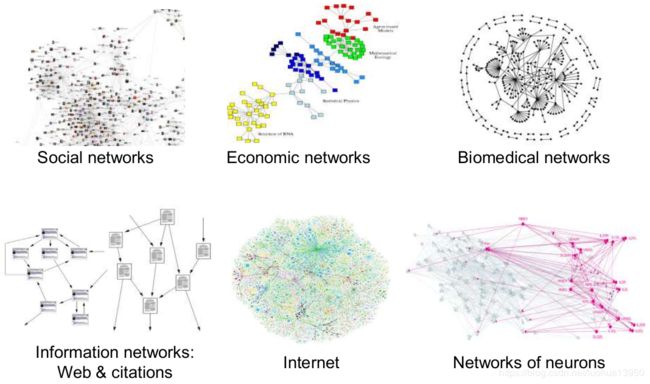
近年来，人们对深度学习方法在图数据上的扩展越来越感兴趣。很多数据都是图结构，例如社交网络、经济网络、生物医学网络、信息网络（互联网网站、学术引用）、互联网、神经网络。而网络是它们的通用语言，因此具备极大的研究价值。在深度学习的成功推动下，研究人员借鉴了卷积网络、循环网络和深度自动编码器的思想，定义和设计了用于处理图数据的神经网络结构，由此衍生出一个新的研究热点——“图神经网络（Graph Neural Networks，GNN）”本篇文章就从图的概述入手开始我们的GNN之路。

1.1 图的基本定义

图(G)定义为(V,E) ，记为G=(V,E) 。
其中： V是顶点(Vertex)的非空有限集合，记为V(G)；E是无序集V&V的一个子集，记为E(G) 。
将顶点集合为空的图称为空图。其形式化定义为：

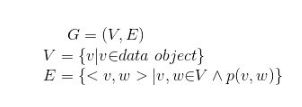
1.1.1　图的基本类型

• 有向图与无向图 （边是否有方向）
• 非加权图与加权图（边是否有权重）
• 连通图与非连通图（是否有孤立顶点）
• 二部图 （任意边均从属于其2个子图）
  
  

1.1.2　邻居和度

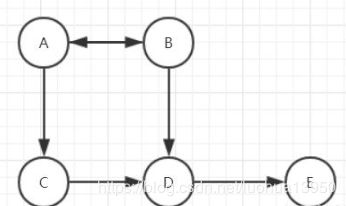
邻居：与顶点A相连接的顶点B和顶点C都是A的邻居
度：顶点A的边的数量（包括出度2与入度1）

1.1.3　子图与路径

子图：设G=(V，E)是一个图，若V’是V的子集，E’是E的子集，且E’中的边所关联的顶点均在V’中，则G’=(V’，E’)也是一个图，并称其为G的子图(Subgraph)。
路径：从顶点V1到顶点V2的边的数目，最少的路径成为顶点的距离

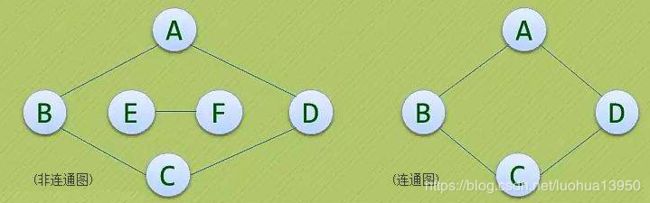
• 无向图的路径
  在无向图G中，若存在一个顶点序列vp,vi1,vi2,…,vim,vq，使得(vp，vi1)，(vi1，vi2)，…，(vim，vq)均属于E(G)，则称顶点vp到vq存在一条路径(Path)。

• 有向图的路径
  在有向图G中，路径也是有向的,它由E(G)中的有向边，，…，组成。

• 路径长度
  路径长度定义为该路径上边的数目。

• 简单路径
  若一条路径上除了vp和vq可以相同外，其余顶点均不相同，则称此路径为一条简单路径。
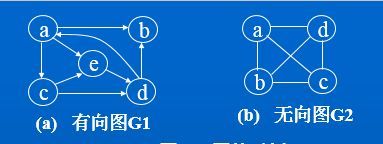
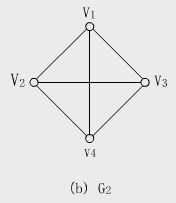
  如图G2中顶点序列vl，v2，v3，v4是一条从顶点v1到顶点v4的长度为3的简单路径；顶点序列v1，v2，v4，v1，v3是一条从顶点v1到顶点v3的长度为4的路径，但不是简单路径；

• 简单回路或简单环(Cycle)
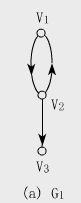
  起点和终点相同(vp=vq)的简单路径称为简单回路或简单环(Cycle)。
  如图G2中，顶点序列v1，v2，v4，v1是一个长度为3的简单环；有向图G1中，顶点序列v1，v2，v1是一长度为2的有向简单环。

• 有根图和图的根
  在一个有向图中，若存在一个顶点v，从该顶点有路径可以到达图中其它所有顶点，则称此有向图为有根图，v称作图的根。

1.2 图的存储与遍历

1.2.1　邻接矩阵与关联矩阵

K阶邻居：V1通过k条边到达顶点V2，V2为V1的k阶邻居
邻接矩阵：N个顶点组成的2维度关系矩阵
关联矩阵：N个顶点与M条边组成的2维度关系矩阵。关联矩阵M(D)=(m_ij)_n×ε的元素m_ij定义为：


上图的邻接矩阵和关联矩阵分别是:

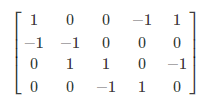
1.2.2　图的遍历

图的遍历：从某顶点出发，沿着图中的边对所有顶点访问一次且仅访问一次。
包括深度优先（DFS）与广度优先（BFS）

• 深度优先遍历（deep first traverse）
  所谓深度优先就是以纵向优先的方式遍历节点。我们从当前节点curr出发，如果当前节点被访问过，就返回，否则将该节点标记为访问过的节点，然后在递归访问当前节点的所有邻接节点。

 function traverse（Node node）｛    //递归方式实现的深度优先遍历
              if(node.isVisited){    //如果当前节点已经被访问过
                  return;            //这个是递归出口
              }
              node.isVisited=true;   //将当前节点置为已经访问
              for(var i=0;i<node.brother.length;i++){
                  traverse(node.brother[i]);   //访问当前node的所有邻接节点
              }
              return;       //结束
          ｝

• 广度有限遍历（broad first traverse）
  所谓的广度优先指的是从当前节点curr出发，将该节点标记为已经访问过的节点，然后在依次访问curr的没有被访问的邻接节点，然后在依次访问邻接节点的邻接节点，直到所有的节点被访问。

function bft(Node node){
	var queue=[],temp; //队列结构，是待访问的节点队列，这些节点被排了顺序，按顺序被访问
             queue.push(node); //初始化队列结构
             while(queue.isNotEmpty())｛   //当队列不为空的时候
                temp=queue.shift();            //取得当前的节点元素
                temp.isVisited=true;           //将当前节点置为已经访问
                for(var i=0;i<temp.brother.length;i++){
                    if(!temp.brother[i].isVisited){   //如果当前节点的邻接节点没有被访问过
                        queue.push(temp.brother[i]);  //将这个邻接节点加入待访问队列
                    }
                }
             ｝
         }

==1.3 图数据的应用场景 ==

比起传统的信息存储和组织模式，图数据库能够很清晰揭示复杂的模式，尤其在错综复杂的社交，物流，金融风控行业效果更为明显。

百花齐放的图数据库，有Operational 图数据库、RDF图数据库、多模式图数据、分析及大图数据库，图数据库的关注度越来越多，并且大都是有持续在更新。

1.图数据类型：
1). 同构图：图中的节点类型与关系类型都仅有1种，如万维网
2). 异构图：图中的节点类型与关系类型都多余1种，关系复杂，更贴近现实
3). 属性图：相对异构图，对数据添加属性（标签与属性）
4). 非显示图：数据之间没有显示地定义关系。

2.图的应用例：
1). 社交网络（人与人）
2). 电子购物（人与物）
3). 化学分子（元素与元素）
4). 交通网络（站点之间）
5). 电路设计图（元器件间）

3.GNN的分类任务：
* 节点分类：如通过引用网络对论文节点分类
* 边分类及预测：如预测社交网络中的2人关系，并进行推荐
* 图分类、表示、生成任务：如药物分子的分类，酶的分类等

总结

本次分享回顾了关于图的基本概述以及用于描述图的最基本的属性。下一篇文章我们将给出详细的Python 示例，从代码的角度深入理解图的定义、图的存储和图的性质：

结束

更多内容请关注从今天开始种树
关注知识图谱与大数据公众号，获取更多内容。