带你玩转Visual Studio——性能分析与优化

上一篇文章带你玩转Visual Studio——VC++的多线程开发讲了VC++中多线程的主要用法。多线程是提升性能和解决并发问题的有效途经。在商用程序的开发中，性能是一个重要的指标，程序的性能优化也是一个重要的工作。

---

找到性能瓶颈

二八法则适合很多事物：最重要的只占其中一小部分，约20%，其余80%的尽管是多数，却是次要的。在程序代码中也是一样，决定应用性能的就那20%的代码(甚至更少)。因此优化实践中，我们将精力集中优化那20%最耗时的代码上，这那20%的代码就是程序的性能瓶颈，主要针对这部分代码进行优化。

常见优化方法：

这部分我就不写，直接参见《性能调优攻略》，因为我没有自信能写出比这更好的。

如果不想这么深入地了解，看看《C++程序常见的性能调优方式》这篇文章也是不错的。

应用案例

我们以一个应用案例来讲解，以至于不会那么乏味难懂。

我们知道能被1和它本身整除的整数叫质数，假设1到任意整数N的和为Sn(Sn=1+2+3+…+n)。现在要求10000到100000之间所有质数和Sn。

可能你会觉得这问题不是So Easy吗！都不用脑袋想，咣当一下就把代码写完了，代码如下：

#include 
#include 

// 定义64位整形
typedef __int64 int64_t;

// 获取系统的当前时间，单位微秒(us)
int64_t GetSysTimeMicros()
{
    // 从1601年1月1日0:0:0:000到1970年1月1日0:0:0:000的时间(单位100ns)
#define EPOCHFILETIME   (116444736000000000UL)
    FILETIME ft;
    LARGE_INTEGER li;
    int64_t tt = 0;
    GetSystemTimeAsFileTime(&ft);
    li.LowPart = ft.dwLowDateTime;
    li.HighPart = ft.dwHighDateTime;
    // 从1970年1月1日0:0:0:000到现在的微秒数(UTC时间)
    tt = (li.QuadPart - EPOCHFILETIME) / 10;
    return tt;
}

// 计算1到n之间所有整数的和
int64_t CalculateSum(int n)
{
    if (n < 0)
    {
        return -1;
    }

    int64_t sum = 0;
    for (int i = 0; i < n; i++)
    {
        sum += i;
    }
    return sum;
}

// 判断整数n是否为质数
bool IsPrime(int n)
{
    if (n < 2)
    {
        return false;
    }

    for (int i = 2; i < n; i++)
    {
        if (n %i == 0)
        {
            return false;
        }
    }

    return true;
}


void PrintPrimeSum()
{
    int64_t startTime = GetSysTimeMicros();
    int count = 0;
    int64_t sum = 0;
    for (int i = 10000; i <= 100000; i++)
    {
        if (IsPrime(i))
        {
            sum = CalculateSum(i);
            std::cout << sum << "\t";
            count++;
            if (count % 10 == 0)
            {
                std::cout << std::endl;
            }
        }
    }
    int64_t usedTime = GetSysTimeMicros() - startTime;
    int second = usedTime / 1000000;
    int64_t temp = usedTime % 1000000;
    int millise = temp / 1000;
    int micros = temp % 1000;
    std::cout << "执行时间:" << second << "s " << millise << "' " << micros << "''" << std::endl;
}

然后一运行，耗时9s 659’ 552”(9秒659毫秒552微秒)。我想这肯定不是你要的结果(太慢了)，如果你觉得还满意，那下面的就可以不用看了。

VS的性能分析工具

性能分析工具的选择

打开一个“性能分析”的会话:Debug->Start Diagnotic Tools Without Debugging(或按Alt+F2)，VS2013在Analysis菜单中。

性能分析

CPU Usage

检测CPU的性能，主要用于发现影响CPU瓶颈(消耗大量CPU资源)的代码。

GPU Usage

检测GPU的性能，常用于图形引擎的应用(如DirectX程序)，主要用于判断是CPU还是GPU的瓶颈。

Memory Usage

检测应用程序的内存，发现内存。

Performance Wizard

性能(监测)向导，综合检测程序的性能瓶颈。这个比较常用，下面再逐一说明。

性能(监测)向导

1. 指定性能分析方法；
   
   性能分析方法
   CPU Sampling(CPU采样)：
   进行采样统计，以低开销水平监视占用大量CPU的应用程序。这个对于计算量大的程序可大大节省监控时间。
   Instrumentation(检测)：
   完全统计，测量函数调用计数和用时
   .NET memory allocation(.NET 内存分配)：
   跟踪托管内存分配。这个好像只有托管代码(如C#)才可用，一般以C++代码好像不行。
   Resource contention data(并发)：
   检测等待其他线程的线程，多用于多线程的并发。
2. 选择要检测的模块或应用程序；
3. 启动分析程序进行监测。

性能分析报告

程序分析完成之后会生成一个分析报告，这就是我们需要的结果。

性能分析报告概要

视图类型

有几个不同的视图可供我们切换，下面加粗的部分是个人觉得比较方便和常用的视图。
Summary(概要):整个报告概要说明
Call Tree(调用树):以树形表格的方式展开函数之间的关系。
Module(模块):分析调用的不同的程序模块，如不同的DLL、lib模块的耗时
Caller/Callee(调用与被调用):以数值显示的调用与被调用的关系
Functions(函数统计):以数值显示的各个函数的执行时间和执行次数统计值
Marks(标记):
Processers(进程):
Function Detials(函数详情):以图表的方式形象地显示：调用函数-当前函数-被调用子函数之间的关系和时间比例。

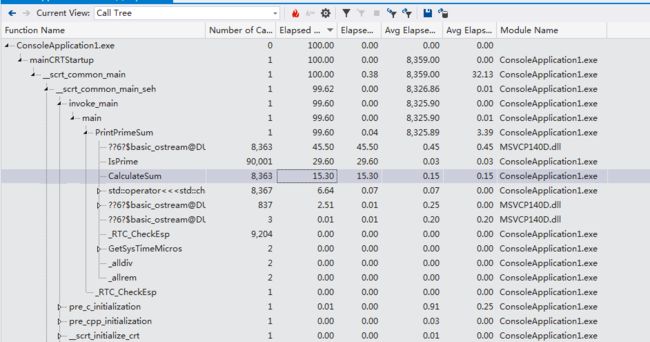
调用树

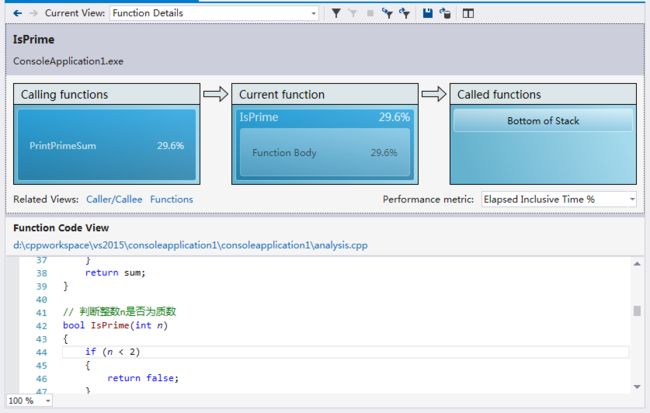
函数详情

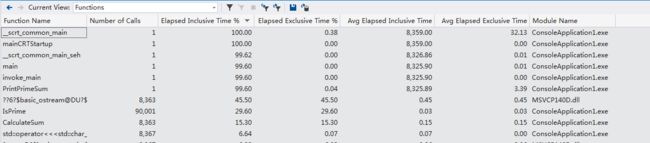
函数统计

专用术语

如果是第一次看这报告，你还不一定能看懂。你需要先了解一些专用术语(你可以对照着Call Tree视图和Functions视图去理解)：
Num of Calls:(函数)调用次数
Elapsed Inclusive Time:已用非独占时间
Elapsed Exclusive Time:已用独占时间
Avg Elapsed Inclusive Time:平均已用非独占时间
Avg Elapsed Exclusive Time:平均已用独占时间
Module Name:模块名称，一般为可执行文件(.exe)、动态库(.dll)、静态库(.lib)的名称。

也许看完你还迷糊，只要理解什么是独占与非独占你就都明白了。

什么是独占与非独占

非独占样本数是指的包括了子函数执行时间的总执行时间
独占样本数是不包括子函数执行时间的函数体执行时间，函数执行本身花费的时间，不包括子(函数)树执行的时间。

解决应用案例问题

我们已经大致了解了VS2015性能分析工具的使用方法。现在回归本质，解决上面提及的应用案例的问题。

1、我们选择Function Detials视图，从根函数开始依据百分比最大的项选择，直到选择PrintPrimeSum，这时可以看到如下图：

找出性能瓶颈1
我们可以看到IO占了50%多(49.4%+9.7%)的时间，所以IO是最大的性能瓶颈。其实，有一定编程经验的人应该都能明白，在控制台输出信息是很耗时的。我们只是需要结果，不一定非要在控制中全部输出(这样还不便查看)，我们可以将结果保存到文件，这样也比输出到控制台快。

注：上图所示的时间，应该是非独占时间的百分比。

知道了瓶颈，就改进行代码优化吧：

void PrintPrimeSum()
{
    int64_t startTime = GetSysTimeMicros();
    std::ofstream outfile;
    outfile.open("D:\\Test\\PrimeSum.dat", std::ios::out | std::ios::app);
    int count = 0;
    int64_t sum = 0;
    for (int i = 10000; i <= 100000; i++)
    {
        if (IsPrime(i))
        {
            sum = CalculateSum(i);
            outfile << sum << "\t";
            count++;
            if (count % 10 == 0)
            {
                outfile << std::endl;
            }
        }
    }
    outfile.close();
    int64_t usedTime = GetSysTimeMicros() - startTime;
    int second = usedTime / 1000000;
    int64_t temp = usedTime % 1000000;
    int millise = temp / 1000;
    int micros = temp % 1000;
    std::cout << "执行时间:" << second << "s " << millise << "' " << micros << "''" << std::endl;
}

再次执行，发现时间一下减小到：3s 798’ 218”。效果很明显！

---

2、但这还不够，继续检查别的问题，对新代码再次用性能分析工具检测一下。

找出性能瓶颈2

我们发现IsPrime函数占用了62%的时间，这应该是一个瓶颈，我们能不能对其进行算法的优化？仔细想想，上面求质数的方法其实是最笨的方法，稍微对其进行优化一下：

// 判断整数n是否为质数
bool IsPrime(int n)
{
    if (n < 2)
    {
        return false;
    }

    if (n == 2)
    {
        return true;
    }

    //把2的倍数剔除掉
    if (n%2 == 0)
    {
        return false;
    }

    // 其实不能被小于n的根以下的数整除，就是一个质数
    for (int i = 3; i*i <= n; i += 2)
    {
        if (n % i == 0)
        {
            return false;
        }
    }

    return true;
}

再次执行，发现时间一下减小到：1s 312’ 75”，几乎减了一半的时间。

3、这还是有点慢，再看看还能不能进行优化。对新代码再次用性能分析工具检测一下。

找出性能瓶颈2

CalculateSum函数占了88.5%的时间，这绝对是影响目前程序性能的主要因素。对其进行。仔细想想，求1到N的和其实就是求1、2、3 … N的等差数列的和。优化代码如下：

// 计算1到n之间所有整数的和
int64_t CalculateSum(int n)
{
    if (n < 0)
    {
        return -1;
    }

    //(n * (1 + n)) / 2
    return ( n * (1 + n) ) >> 1;
}

再次执行，发现时间一下减小到：0s 91’ 6”，一秒中之内，基本上可以满足要求子。

总结

程序性能调优，就是数上面这样一点点地改进的过程，直到满足应用的要求。上面只用了一个视图的一种统计指标(各函数所用时间占总时间的百分比)，就解决了问题。对于大型的复杂应用程序，我们可以结果多种视图的多种统计指标进行综合判断，找出程序性能的瓶颈！

---

---

上一篇回顾：
带你玩转Visual Studio——VC++的多线程开发

下一篇要讲述的内容：
带你玩转Visual Studio——单元测试

---

---