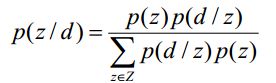机器学习代码整理pLSA、BoW、DBN、DNN

机器学习代码整理pLSA、BoW、DBN、DNN

2015年05月19日 11:13:00 曼陀罗彼岸花 阅读数：2946

 

丕子同学整理点自己的代码：Lp_LR、Pagerank(MapReduce)、pLSA、BoW、DBN、DNN

 

听说如果你在github等代码托管平台上有自己的开源工具，可以写进简历，是一个加分~

那就整理整理之前的一些代码片段。

PG_ROC_PR_R：R语言绘制ROC和PR曲线。R

PG_PageRank：mapreduce版本的pagerank计算方法。Shell awk

PG_LINEAR：L_p-Regularized logistic regression using Gradient Decent;  Shell awk

PG_Curve:matlab绘制roc、pr等曲线以及计算结果； Matlab

PG_BOW_DEMO：图像分类demo，特征为bow。 Matlab

PG_PLSA ： pLSA demo， python

PG_DEEP：Deep Learning and Applications--Demo；C++

来自：http://www.zhizhihu.com/html/y2013/4335.html

 

 

====================================================================================================================================================================================================================================================================================================================================================================

 

 

一. LSA

1. LSA原理

LSA(latent semantic analysis)潜在语义分析，也被称为 LSI(latent semantic index)，是 Scott Deerwester, Susan T. Dumais 等人在 1990 年提出来的一种新的索引和检索方法。该方法和传统向量空间模型(vector space model)一样使用向量来表示词(terms)和文档(documents)，并通过向量间的关系(如夹角)来判断词及文档间的关系；不同的是，LSA 将词和文档映射到潜在语义空间，从而去除了原始向量空间中的一些“噪音”，提高了信息检索的精确度。

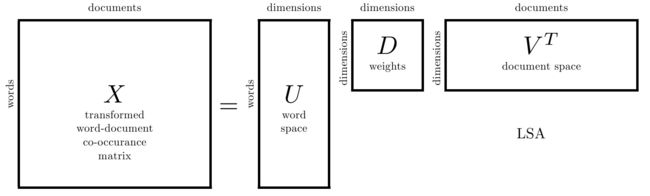
引用吴军老师在 “矩阵计算与文本处理中的分类问题” 中的总结：

三个矩阵有非常清楚的物理含义。第一个矩阵 U 中的每一行表示意思相关的一类词，其中的每个非零元素表示这类词中每个词的重要性（或者说相关性），数值越大越相关。最后一个矩阵 V 中的每一列表示同一主题一类文章，其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵 D 则表示类词和文章类之间的相关性。因此，我们只要对关联矩阵 X 进行一次奇异值分解，我们就可以同时完成了近义词分类和文章的分类。（同时得到每类文章和每类词的相关性）。

传统向量空间模型使用精确的词匹配，即精确匹配用户输入的词与向量空间中存在的词，无法解决一词多义(polysemy)和一义多词(synonymy)的问题。实际上在搜索中，我们实际想要去比较的不是词，而是隐藏在词之后的意义和概念。

LSA 的核心思想是将词和文档映射到潜在语义空间，再比较其相似性。

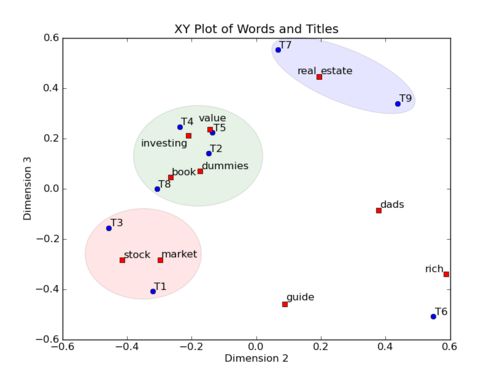
举个简单的栗子，对一个 Term-Document 矩阵做SVD分解，并将左奇异向量和右奇异向量都取后2维（之前是3维的矩阵），投影到一个平面上（潜在语义空间），可以得到：

在图上，每一个红色的点，都表示一个词，每一个蓝色的点，都表示一篇文档，这样我们可以对这些词和文档进行聚类，比如说 stock 和 market 可以放在一类，因为他们老是出现在一起，real 和 estate 可以放在一类，dads，guide 这种词就看起来有点孤立了，我们就不对他们进行合并了。按这样聚类出现的效果，可以提取文档集合中的近义词，这样当用户检索文档的时候，是用语义级别（近义词集合）去检索了，而不是之前的词的级别。这样一减少我们的检索、存储量，因为这样压缩的文档集合和PCA是异曲同工的，二可以提高我们的用户体验，用户输入一个词，我们可以在这个词的近义词的集合中去找，这是传统的索引无法做到的。

2. LSA的优点

1）低维空间表示可以刻画同义词，同义词会对应着相同或相似的主题。

2）降维可去除部分噪声，是特征更鲁棒。

3）充分利用冗余数据。

4）无监督/完全自动化。

5）与语言无关。

3. LSA的缺点

1）LSA可以处理向量空间模型无法解决的一义多词(synonymy)问题，但不能解决一词多义(polysemy)问题。因为LSA将每一个词映射为潜在语义空间中的一个点，也就是说一个词的多个意思在空间中对于的是同一个点，并没有被区分。

2）SVD的优化目标基于L-2 norm 或者 Frobenius Norm 的，这相当于隐含了对数据的高斯分布假设。而 term 出现的次数是非负的，这明显不符合 Gaussian 假设，而更接近 Multi-nomial 分布。

3）特征向量的方向没有对应的物理解释。

4）SVD的计算复杂度很高，而且当有新的文档来到时，若要更新模型需重新训练。

5）没有刻画term出现次数的概率模型。

6）对于count vectors 而言，欧式距离表达是不合适的（重建时会产生负数）。

7）维数的选择是ad-hoc的。

 

二. pLSA

首先，我们可以看看日常生活中人是如何构思文章的。如果我们要写一篇文章，往往是先确定要写哪几个主题。譬如构思一篇自然语言处理相关的文章，可能40%会谈论语言学，30%谈论概率统计，20%谈论计算机，还有10%谈论其它主题。

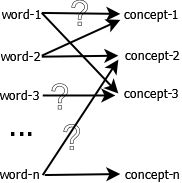
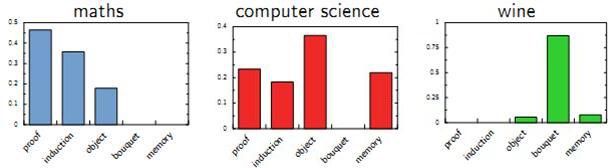
对于语言学，容易想到的词包括：语法，句子，主语等；对于概率统计，容易想到的词包括：概率，模型，均值等；对于计算机，容易想到的词包括：内存，硬盘，编程等。我们之所以能想到这些词，是因为这些词在对应的主题下出现的概率很高。我们可以很自然的看到，一篇文章通常是由多个主题构成的，而每一个主题大概可以用与该主题相关的频率最高的一些词来描述。以上这种想法由Hofmann于1999年给出的pLSA模型中首先进行了明确的数学化。Hofmann认为一篇文章（Doc）可以由多个主题（Topic）混合而成，而每个Topic都是词汇上的概率分布，文章中的每个词都是由一个固定的Topic生成的。下图是英语中几个Topic的例子。

 

pLSA的建模思路分为两种。

1. 第一种思路

以的概率从文档集合中选择一个文档

以的概率从主题集合中选择一个主题

以的概率从词集中选择一个词

有几点说明：

• 以上变量有两种状态：observed ( & 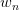) 和 latent ()
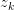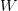• 来自文档，但同时是集合（元素不重复），相当于一个词汇表

直接的，针对observed variables做建立likelihood function：

其中，为pair出现的次数。为加以区分，之后使用与标识对应文档与词汇数量。两边取，得：

其中，倒数第二步旨在将暴露出来。由于likelihood function中与存在latent variable，难以直接使用MLE求解，很自然想到用E-M算法求解。E-M算法主要分为Expectation与Maximization两步。

 Step 1: Expectation

假设已知与，求latent variable的后验概率

Step 2: Maximization

求关于参数和的Complete data对数似然函数期望的极大值，得到最优解。带入E步迭代循环。

由式可得：

此式后部分为常量。故令：

建立以下目标函数与约束条件：

只有等式约束，使用Lagrange乘子法解决：

对与求驻点，得：

令，得：

，故有：

同理，有：

将与回代Expectation：

，循环迭代。

pLSA的建模思想较为简单，对于observed variables建立likelihood function，将latent variable暴露出来，并使用E-M算法求解。其中M步的标准做法是引入Lagrange乘子求解后回代到E步。

 

总结一下使用EM算法求解pLSA的基本实现方法：

(1)E步骤：求隐含变量Given当前估计的参数条件下的后验概率。

(2)M步骤：最大化Complete data对数似然函数的期望，此时我们使用E步骤里计算的隐含变量的后验概率，得到新的参数值。

两步迭代进行直到收敛。

2. 第二种思路

这个思路和上面思路的区别就在于对P(d,w)的展开公式使用的不同，思路二使用的是3个概率来展开的，如下：

这样子我们后面的EM算法的大致思路都是相同的，就是表达形式变化了，最后得到的EM步骤的更新公式也变化了。当然，思路二得到的是3个参数的更新公式。如下：

 

 你会发现，其实多了一个参数是P(z)，参数P（d|z）变化了（之前是P(z|d)），然后P(w|z)是不变的，计算公式也相同。

给定一个文档d，我们可以将其分类到一些主题词类别下。

PLSA算法可以通过训练样本的学习得到三个概率，而对于一个测试样本，其中P(w|z)概率是不变的，但是P(z)和P(d|z)都是需要重新更新的，我们也可以使用上面的EM算法，假如测试样本d的数据，我们可以得到新学习的P(z)和P(d|z)参数。这样我们就可以计算：

为什么要计算P(z|d)呢？因为给定了一个测试样本d，要判断它是属于那些主题的，我们就需要计算P(z|d)，就是给定d，其在主题z下成立的概率是多少，不就是要计算吗。这样我们就可以计算文档d在所有主题下的概率了。

这样既可以把一个测试文档划归到一个主题下，也可以给训练文档打上主题的标记，因为我们也是可以计算训练文档它们的的。如果从这个应用思路来说，思路一说似乎更加直接，因为其直接计算出来了。

3. pLSA的优势

1）定义了概率模型，而且每个变量以及相应的概率分布和条件概率分布都有明确的物理解释。

2）相比于LSA隐含了高斯分布假设，pLSA隐含的Multi-nomial分布假设更符合文本特性。

3）pLSA的优化目标是是KL-divergence最小，而不是依赖于最小均方误差等准则。

4）可以利用各种model selection和complexity control准则来确定topic的维数。

4. pLSA的不足

 

1）概率模型不够完备：在document层面上没有提供合适的概率模型，使得pLSA并不是完备的生成式模型，而必须在确定document i的情况下才能对模型进行随机抽样。

2）随着document和term 个数的增加，pLSA模型也线性增加，变得越来越庞大。

3）EM算法需要反复的迭代，需要很大计算量。

 

针对pLSA的不足，研究者们又提出了各种各样的topic based model, 其中包括大名鼎鼎的Latent Dirichlet Allocation (LDA)。

 

三. pLSA的Python代码实现

1. preprocess.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
class Preprocess:
    def __init__(self, fname, fsw):
        self.fname = fname
        # doc info
        self.docs = []
        self.doc_size = 0
        # stop word info
        self.sws = []
        # word info
        self.w2id = {}
        self.id2w = {}
        self.w_size = 0
        # stop word list init
        with open(fsw, 'r') as f:
            for line in f:
                self.sws.append(line.strip())
    def __work(self):
        with open(self.fname, 'r') as f:
            for line in f:
                line_strip = line.strip()
                self.doc_size += 1
                self.docs.append(line_strip)
                items = line_strip.split()
                for it in items:
                    if it not in self.sws:
                        if it not in self.w2id:
                            self.w2id[it] = self.w_size
                            self.id2w[self.w_size] = it
                            self.w_size += 1
        self.w_d = np.zeros([self.w_size, self.doc_size], dtype=np.int)
        for did, doc in enumerate(self.docs):
            ws = doc.split()
            for w in ws:
                if w in self.w2id:
                    self.w_d[self.w2id[w]][did] += 1
    def get_w_d(self):
        self.__work()
        return self.w_d
    def get_word(self, wid):
        return self.id2w[wid]
if __name__ == '__main__':
    fname = './data.txt'
    fsw = './stopwords.txt'
    pp = Preprocess(fname, fsw)

2. plsa.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
import time
import logging
def normalize(vec):
    s = sum(vec)
    for i in range(len(vec)):
        vec[i] = vec[i] * 1.0 / s
def llhood(w_d, p_z, p_w_z, p_d_z):
    V, D = w_d.shape
    ret = 0.0
    for w, d in zip(*w_d.nonzero()):
        p_d_w = np.sum(p_z * p_w_z[w,:] * p_d_z[d,:])
        if p_d_w > 0:
            ret += w_d[w][d] * np.log(p_d_w)
    return ret
class PLSA:
    def __init__(self):
        pass
    def train(self, w_d, Z, eps):
        V, D = w_d.shape
        # create prob array, p(d|z), p(w|z), p(z)
        p_d_z = np.zeros([D, Z], dtype=np.float)
        p_w_z = np.zeros([D, Z], dtype=np.float)
        p_z = np.zeros([Z], dtype=np.float)
        # initialize
        p_d_z = np.random.random([D, Z])
        for d_idx in range(D):
            normalize(p_d_z[d_idx])
        p_w_z = np.random.random([V, Z])
        for w_idx in range(V):
            normalize(p_w_z[w_idx])
        p_z = np.random.random([Z])
        normalize(p_z)
        # iteration until converge
        step = 1
        pp_d_z = p_d_z.copy()
        pp_w_z = p_w_z.copy()
        pp_z = p_z.copy()
        while True:
            logging.info('[ iteration ] step %d' % step)
            step += 1
            p_d_z *= 0.0
            p_w_z *= 0.0
            p_z *= 0.0
            # run EM algorithm
            for w_idx, d_idx in zip(*w_d.nonzero()):
                #print '[ EM ] >>>>>> E step : '
                p_z_d_w = pp_z * pp_d_z[d_idx,:] * pp_w_z[w_idx,:]
                normalize(p_z_d_w)
                #print '[ EM ] >>>>>> M step : '
                tt = w_d[w_idx, d_idx] * p_z_d_w
                p_w_z[w_idx,:] += tt
                p_d_z[d_idx,:] += tt
                p_z += tt
            normalize(p_w_z)
            normalize(p_d_z)
            p_z = p_z / w_d.sum()
            # check converge
            l1 = llhood(w_d, pp_z, pp_w_z, pp_d_z)
            l2 = llhood(w_d, p_z, p_w_z, p_d_z)
            diff = l2 - l1
            logging.info('[ iteration ] l2-l1  %.3f - %.3f = %.3f ' % (l2, l1, diff))
            if abs(diff) < eps:
                logging.info('[ iteration ] End EM ')
                return (l2, p_d_z, p_w_z, p_z)
            pp_d_z = p_d_z.copy()
            pp_w_z = p_w_z.copy()
            pp_z = p_z.copy()

3. main.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-
from preprocess import Preprocess as PP
from plsa import PLSA
import numpy as np
import logging
import time
def main():
    # setup logging --------------------------
    logging.basicConfig(filename='plsa.log',
                        level=logging.INFO,
                        format='%(asctime)s %(filename)s[line:%(lineno)d] %(levelname)s %(message)s',
                        datefmt='%a, %d %b %Y %H:%M:%S')
    #console = logging.StreamHandler()
    #console.setLevel(logging.INFO)
    #logging.getLogger('').addHandler(console)
    # some basic configuration ---------------
    fname = './data.txt'
    fsw = './stopwords.txt'
    eps = 20.0
    key_word_size = 10
    # preprocess -----------------------------
    pp = PP(fname, fsw)
    w_d = pp.get_w_d()
    V, D = w_d.shape
    logging.info('V = %d, D = %d' % (V, D))
    # train model and get result -------------
    pmodel = PLSA()
    for z in range(3, (D+1), 10):
        t1 = time.clock()
        (l, p_d_z, p_w_z, p_z) = pmodel.train(w_d, z, eps)
        t2 = time.clock()
        logging.info('z = %d, eps = %f, time = %f' % (z, l, t2-t1))
        for itz in range(z):
            logging.info('Topic %d' % itz)
            data = [(p_w_z[i][itz], i) for i in range(len(p_w_z[:,itz]))]
            data.sort(key=lambda tup:tup[0], reverse=True)
            for i in range(key_word_size):
                logging.info('%s : %.6f ' % (pp.get_word(data[i][1]), data[i][0]))
if __name__ == '__main__':
    main()

 

版权声明：

   本文由笨兔勿应所有，发布于http://www.cnblogs.com/bentuwuying。如果转载，请注明出处，在未经作者同意下将本文用于商业用途，将追究其法律责任。

 

==================================================================================================================================================================================

http://blog.tomtung.com/2011/10/plsa/

 

 

==================================================================================================================================================================================

 

Probabilistic latent semantic analysis (pLSA)

statistics algorithm machine learning topic model

Probabilistic latent semantic analysis (概率潜在语义分析，pLSA) 是一种 Topic model，在99年被 Thomas Hofmann 提出。它和随后提出的 LDA 使得 Topic Model 成为了研究热点，其后的模型大都是建立在二者的基础上的。

我们有时会希望在数量庞大的文档库中自动地发现某些结构。比如我们希望在文档库发现若干个“主题”，并将每个主题用关键词的形式表现出来。 我们还希望知道每篇文章中各个主题占得比重如何，并据此判断两篇文章的相关程度。而 pLSA 就能完成这样的任务。

我之前取了 Wikinews 中的 1000 篇新闻，试着用 pLSA 在其中发现 K=15 个主题。比如一篇关于 Wikileaks 的阿萨奇被保释消息的新闻，算法以 100% 的概率把它分给了主题 9，其关键词为：

media phone hacking wikileaks assange australian stated information investigation murdoch

可以看到这个主题的发现还是非常靠谱的。又比如这条中国人民的老朋友威胁要大打打核战争 的新闻。 算法把它以 97.7% 的概率分给了主题 3，2.3% 的概率分给了主题 7。主题 3 的关键词是：

south north court china military death tornado service million storm

主题 7 的关键词是：

nuclear plant power japan million carbon radiation china water minister

可以看到这条新闻和主题 3 中的“南北”、“军事”、“中国”、“死亡”这些信息联系在一起，和主题 7 中的“核”、“中国”联系在一起。 应该是因为我的数据集中与北朝鲜核问题相关的新闻只有不到 10 条，而 10 个主题的划分并不够细致，所以关于“朝核问题”或者“核武器”的这样的主题并没能被分离出来。但可以看到即使是这样结果也是很 make sense 的。

那我们就来看看 pLSA 模型是怎么回事吧。和很多模型一样，pLSA 遵从 bag-of-words 假设， 即只考虑一篇文档中单词出现的次数，忽略单词的先后次序关系，且每个单词的出现都是彼此独立的。 这样一来，我们观察到的其实就是每个单词 w∈W

在每篇文档 d∈D 中出现的次数 n(w,d)。 pLSA 还假设对于每对出现的 (d,w) 都对应着一个表示“主题”的隐藏变量 z∈Z。 pLSA 是一个生成模型，它假设 d、w 和 z

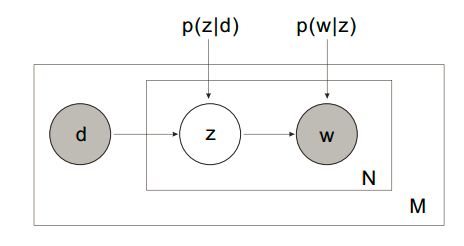
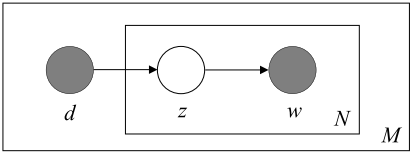
之间的关系用贝叶斯网络表示是这样的（从 [Blei03] 偷的图）：

实心的节点 d

和 w 表示我们能观察到的文档和单词，空心的 z 表示我们观察不到的隐藏变量，用来表示隐含的主题。图中用了所谓的“盘子记法”， 即用方框表示随机变量的重复。这里方框右下角的字母 M 和 N 分别表示有 M 篇文档，第 j 篇文档有 Nj 个单词。每条有向边表示随机变量间的依赖关系。也就是说，pLSA 假设每对 (d,w)

 都是由下面的过程产生的：

1. 以 P(d)

的先验概率选择一篇文档 d

•  
• 选定 d
• 后，以 P(z|d) 的概率选中主题 z
•  
• 选中主题 z
• 后，以 P(w|z) 的概率选中单词 w
  1.  

  而我们感兴趣的正是其中的 P(z|d)

  和 P(w|z)：利用前者我们可以知道每篇文章中各主题所占的比重， 利用后者我们则能知道各单词在各主题中出现的概率，从而进一步找出各主题的“关键词”。记 θ=(P(z|d),P(w|z))， 表示我们希望估计的模型参数。当然 θ 不仅仅代表两个数，而是对于每对 (w(j),z(k)) 和 (d(i),z(k)) ， 我们都要希望知道 P(z(k)|d(i)) 和 P(w(j)|z(k)) 的值。也就是说，模型中共有 |Z|⋅|D|+|W|⋅|Z|

   个参数。我们还知道：

  P(d,w)P(w|d)=P(d)P(w|d)=∑zP(w|z)P(z|d)

  根据最大log似然估计法，我们要求的就是

  argmaxθL(θ)=argmaxθ∑d,wn(d,w)logP(d,w;θ)=argmaxθ∑d,wn(d,w)logP(w|d;θ)P(d)=argmaxθ{∑d,wn(d,w)logP(w|d;θ)+∑d,wn(d,w)logP(d)}

  这里由于 ∑d,wn(d,w)logP(d)

  这一项与 θ 无关，在 argmaxθ

  中可以被直接扔掉。 [1]

  因此

  argmaxθL(θ)=argmaxθ∑d,wn(d,w)logP(w|d;θ)=argmaxθ∑d,wn(d,w)log∑zP(w|z)P(z|d)

  这里出现了 log

  套 ∑ 的形式，导致很难直接拿它做最大似然。但假如能观察到 z，问题就很简单了。于是我们想到根据 EM 算法 （参见我的上篇笔记），可以用下式迭代逼近 argmaxθL(θ)

  ：

  argmaxθQt(θ)=argmaxθ∑d,wn(d,w)Ez|d,w;θt[logP(w,z|d;θ)]

  其中

  Ez|d,w;θt[logP(w,z|d;θ)]=∑zP(z|d,w;θt)logP(w,z|d;θ)=∑zP(z|d,w;θt)[logP(w|z)+logP(z|d)]

  在 E-step 中，我们需要求出 Qt(θ)

  中除 θ 外的其它未知量，也就是说对于每组 (d(i),w(j),z(k)) 我们都需要求出 P(z(k)|d(i),w(j);θt)

  。 根据贝叶斯定理贝叶斯定理，我们知道：

  P(z(k)|d(i),w(j);θt)=Pt(z(k)|d(i))Pt(w(j)|z(k))∑zPt(z|d(i))Pt(w(j)|z)

  而 Pt(z|d)

  和 Pt(w|z) 就是上轮迭代求出的 θt

  。这样就完成了 E-step。

  接下来 M-step 就是要求 argmaxθQt(θ)

  了。利用基本的微积分工具 [2]，可以分别对每对 (w(j),z(k)) 和 (d(i),z(k))

   求出：

  Pt+1(w(j)|z(k))Pt+1(z(k)|d(i))=∑dn(d,w(j))P(z(k)|d,w(j);θt)∑d,wn(d,w)P(z(k)|d,w;θt)=∑wn(d(i),w)P(z(k)|d(i),w;θt)∑w,zn(d,w)P(z|d(i),w;θt)

  以上就是 pLSA 算法了。最后贴个我用 MATLAB 写的实现 [3]：

  function [p_w_z, p_z_d, Lt] = pLSA(n_dw, n_z, iter_num)
  % PLSA  Fit a pLSA model on given data
  %       in which n_dw(d,w) is the number of occurrence of word w
  %       in document d, d, n_z is the number of topics to be discovered
  %
  
  % pre-allocate space
  [n_d, n_w] = size(n_dw); % max indices of d and w
  p_z_d = rand(n_z, n_d); % p(z|d)
  p_w_z = rand(n_w, n_z); % p(w|z)
  n_p_z_dw = cell(n_z, 1); % n(d,w) * p(z|d,w)
  for z = 1:n_z
      n_p_z_dw{z} = sprand(n_dw);
  end
  
  p_dw = sprand(n_dw); % p(d,w)
  Lt = []; % log-likelihood
  for i = 1:iter_num
      %disp('E-step');
      for d = 1:n_d
          for w = find(n_dw(d,:))
              for z = 1:n_z
                  n_p_z_dw{z}(d,w) = p_z_d(z,d) * p_w_z(w,z) * ...
                      n_dw(d,w) / p_dw(d, w);
              end
          end
      end
  
      %disp('M-step');
      %disp('update p(z|d)')
      concat = cat(2, n_p_z_dw{:}); % make n_p_z_dw{:}(d,:)) possible
      for d = 1:n_d
          for z = 1:n_z
              p_z_d(z,d) = sum(n_p_z_dw{z}(d,:));
          end
          p_z_d(:,d) = p_z_d(:,d) / sum(concat(d,:));
      end
  
      %disp('update p(w|z)')
      for z = 1:n_z
          for w = 1:n_w
              p_w_z(w,z) = sum(n_p_z_dw{z}(:,w));
          end
          p_w_z(:,z) = p_w_z(:,z) / sum(n_p_z_dw{z}(:));
      end
  
      % update p(d,w) and calculate likelihood
      L = 0;
      for d = 1:n_d
          for w = find(n_dw(d,:))
              p_dw(d,w) = 0;
              for z = 1:n_z
                  p_dw(d,w) = p_dw(d,w) + p_w_z(w,z) * p_z_d(z,d);
              end
              L = L + n_dw(d,w) * log(p_dw(d, w));
          end
      end
  
      Lt = [Lt; L];
      %plot(Lt); ylim([2*median(Lt)-L-0.1 L+(L-median(Lt))/2+0.1]);
      %drawnow; pause(0.1)
  end
  
  end
  

  第一次拿 Mablab 写程序，比较丑…… [4]

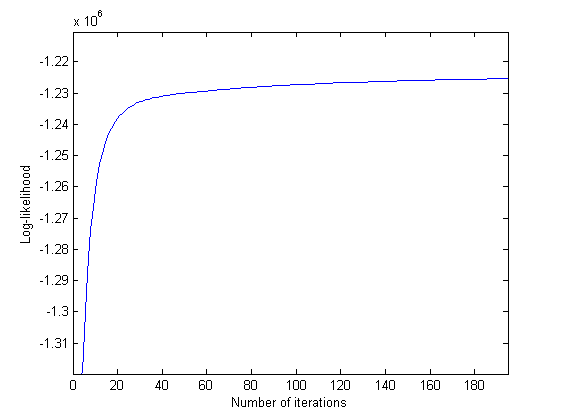
  下图是 Log 似然度随迭代收敛的情况。可以看到收敛速度还是相对较快的。 而且由于是 EM 算法的缘故，Log 似然度确实是单调上升的.

  

  最后，pLSA 的问题是在文档的层面上没有一个概率模型，每篇文档的 P(d|z) 都是需要拟合的模型参数。 这就导致参数的数目会随文档数目线性增长、不能处理训练集外的文档这样的问题。所以02 David Blei、Andrew Ng（就是正在 ml-class.org 里上公开课的那位） 和 Michael Jordan 又提出了一个更为简洁的模型：LDA。有时间的话下次再写了。

  [1]	这里 Hofmann 自己在 [Hofmann99] 和 [Gildea99] 中使用了不同的形式。本文和 Gildea99、[Brants05] 一样选择不去理会 P(d)

  。因为正如 Brants05 中指出、Blei03 及很多其它文献吐槽的那样，Hofmann99 中的模型算出的 P(d) 实在坑爹，当 d 不在训练集中时 P(d) 就一律为0，没什么意义，还不如别估计它呢。另外 (Hofmann, 1999) 中额外引入了一个参数 β

  来“解决”过度拟合问题，但 Brants05 中指出这一问题实际并不存在，因此本文也对此忽略不提。

  [2]	具体而言，这里要求的是 Qt(θ)

  在 ∑wP(w|z)=1 和 ∑zP(z|d)=1

   约束条件下的极值。根据拉格朗日乘数法，解：

  ∇θ(Q(θ)+∑zαz(∑wP(w|z)−1)+∑dβd(∑zP(z|d)−1))=0

  [3]	完整的程序和数据在这里。

  [4]	吐槽：用 Matlab 做简单字符串处理怎么都那么恶心！长度不同的字符串竟然算是不同类型的！Cell array 怎么那么难用！

  [Blei03]

  Blei, D.M. et al. 2003. Latent Dirichlet Allocation. Journal of Machine Learning Research. 3, 4-5 (2003), 993-1022.

  [Hofmann99]

  Hofmann, T. 1999. Probabilistic latent semantic indexing. Proceedings of the 22nd annual international ACM SIGIR conference on Research and development in information retrieval SIGIR 99. pages, (1999), 50-57.

  [Gildea99]

  Gildea, D. and Hofmann, T. 1999. Topic-based language models using EM. Proceedings of the 6th European Conference on Speech (1999), 2167-2170.

  [Brants05]

  Brants, T. 2005. Test Data Likelihood for PLSA Models. Information Retrieval. (2005), 181-196.

 

 

 

 

====================================================================================================================================================================================================================================================================================================================================================================

使用Python自动提取内容摘要

https://www.biaodianfu.com/automatic-text-summarizer.html

利用计算机将大量的文本进行处理，产生简洁、精炼内容的过程就是文本摘要，人们可通过阅读摘要来把握文本主要内容，这不仅大大节省时间，更提高阅读效率。但人工摘要耗时又耗力，已不能满足日益增长的信息需求，因此借助计算机进行文本处理的自动文摘应运而生。近年来，自动摘要、信息检索、信息过滤、机器识别、等研究已成为了人们关注的热点。

自动摘要（Automatic Summarization）的方法主要有两种：Extraction和Abstraction。其中Extraction是抽取式自动文摘方法，通过提取文档中已存在的关键词，句子形成摘要；Abstraction是生成式自动文摘方法，通过建立抽象的语意表示，使用自然语言生成技术，形成摘要。由于自动摘要方法需要复杂的自然语言理解和生成技术支持，应用领域受限。，抽取式摘要成为现阶段主流，它也能在很大程度上满足人们对摘要的需求。

目前抽取式的主要方法：

• 基于统计：统计词频，位置等信息，计算句子权值，再简选取权值高的句子作为文摘，特点：简单易用，但对词句的使用大多仅停留在表面信息。
• 基于图模型：构建拓扑结构图，对词句进行排序。例如，TextRank/LexRank
• 基于潜在语义：使用主题模型，挖掘词句隐藏信息。例如，采用LDA，HMM
• 基于线路规划：将摘要问题转为线路规划，求全局最优解。

2007年，美国学者的论文《A Survey on Automatic Text Summarization》（Dipanjan Das, Andre F.T. Martins, 2007）总结了目前的自动摘要算法。其中，很重要的一种就是词频统计。这种方法最早出自1958年的IBM公司科学家 H.P. Luhn的论文《The Automatic Creation of Literature Abstracts》。

Luhn博士认为，文章的信息都包含在句子中，有些句子包含的信息多，有些句子包含的信息少。”自动摘要”就是要找出那些包含信息最多的句子。句子的信息量用”关键词”来衡量。如果包含的关键词越多，就说明这个句子越重要。Luhn提出用”簇”（cluster）表示关键词的聚集。所谓”簇”就是包含多个关键词的句子片段。

上图就是Luhn原始论文的插图，被框起来的部分就是一个”簇”。只要关键词之间的距离小于”门槛值”，它们就被认为处于同一个簇之中。Luhn建议的门槛值是4或5。也就是说，如果两个关键词之间有5个以上的其他词，就可以把这两个关键词分在两个簇。下一步，对于每个簇，都计算它的重要性分值。

以上图为例，其中的簇一共有7个词，其中4个是关键词。因此，它的重要性分值等于 ( 4 x 4 ) / 7 = 2.3。

然后，找出包含分值最高的簇的句子（比如5句），把它们合在一起，就构成了这篇文章的自动摘要。具体实现可以参见 《Mining the Social Web: Analyzing Data from Facebook, Twitter, LinkedIn, and Other Social Media Sites》（O’Reilly, 2011）一书的第8章，python代码见github。

Luhn的这种算法后来被简化，不再区分”簇”，只考虑句子包含的关键词。下面就是一个例子（采用伪码表示），只考虑关键词首先出现的句子。

类似的算法已经被写成了工具，比如基于Java的Classifier4J库的SimpleSummariser模块、基于C语言的OTS库、以及基于classifier4J的C#实现和python实现。

参考文章：

• http://www.ruanyifeng.com/blog/2013/03/automatic_summarization.html
• http://joshbohde.com/blog/document-summarization

TextTeaser

TextTeaser 原本是为在线长文章（所谓 tl;dr：too long; didn’t read）自动生成摘要的服务，其原本的收费标准是每摘要 1000 篇文章付费 12 美元或每月 250 美元。巴尔宾称 TextTeaser 可以为任何使用罗马字母的文本进行摘要，而且比同类工具如 Cruxbot 和 Summly（在 2013 年 3 月被 雅虎斥资 3000 万美元收购）更准确。其创造者霍洛•巴尔宾（Jolo Balbin）表示，在“发现一些扩展问题，特别是 API 中的问题后”，他决定将 TextTeaser 代码开源。

TextTeaser开源的代码一共有三个class，TextTeaser,Parser,Summarizer。

• TextTeaser，程序入口类。给定待摘要的文本和文本题目，输出文本摘要，默认是原文中最重要的5句话。
• Summarizer，生成摘要类。计算出每句话的分数，并按照得分做排序，然后按照原文中句子的顺序依次输出得分最高的5句话作为摘要。
• Parser，文本解析类。对文本进行去除停用词、去除标点符号、分词、统计词频等一些预处理操作。

其中打分模型分为四部分：

• 句子长度，长度为20的句子为最理想的长度，依照距离这个长度来打分。
• 句子位置，根据句子在全文中的位置，给出分数。（巴尔宾认为一篇文章的第二句比第一句更重要，因为很多作家都习惯到第二句话引入关键点）备注：用段落效果会怎样？
• 文章标题与文章内容的关系，句子是否包含标题词，根据句子中包含标题词的多少来打分。
• 句子关键词打分，文本进行预处理之后，按照词频统计出排名前10的关键词，通过比较句子中包含关键词的情况，以及关键词分布的情况来打分（sbs，dbs两个函数）。

开源版本：

• Scala版本：https://github.com/MojoJolo/textteaser
• Python版本：https://github.com/DataTeaser/textteaser

自己尝试这个调用Python版本。主要：不要使用pip install textteaser进行安装，该安装方式安装的是这个项目：

https://github.com/jgoettsch/py-textteaser，该项目并非算法实现，而是API实现。直接下载代码即可：https://github.com/DataTeaser/textteaser

下载完成后在Windows下运营test.py会报错，报错信息如下：

 

 

1 2 3 4 5 6 7 8 9 10 11 12

Traceback (most recent call last):   File "D:/textteaser/test.py", line 12, in     sentences = tt.summarize(title, text)   File "D:\textteaser\textteaser\__init__.py", line 13, in summarize     result = self.summarizer.summarize(text, title, source, category)   File "D:\textteaser\textteaser\summarizer.py", line 11, in summarize     sentences = self.parser.splitSentences(text)   File "D:\textteaser\textteaser\parser.py", line 62, in splitSentences     tokenizer = nltk.data.load('file:' + os.path.dirname(os.path.abspath(__file__)) + '/trainer/english.pickle')   File "C:\Python27\lib\site-packages\nltk\data.py", line 806, in load     resource_val = pickle.load(opened_resource) ImportError: No module named copy_reg

针对报错信息，做如下修改：

1、将”D:\textteaser\textteaser\parser.py”第62行进行修改：

 

 

1 2	#tokenizer = nltk.data.load('file:' + os.path.dirname(os.path.abspath(__file__)) + '/trainer/english.pickle') tokenizer = nltk.data.load('file:' + os.path.dirname(os.path.abspath(__file__)) + os.sep + 'trainer' + os.sep + 'english.pickle')

2、找到”\Lib\site-packages\nltk\data.py”第924行，将

 

 

1	return find(path_, ['']).open()

修改为：

 

 

1 2 3 4 5 6 7 8 9

file_path = find(path_, [''])         data = open(file_path, 'rb').read()         newdata = data.replace("\r\n", "\n")         if newdata != data:             f = open(file_path, "wb")             f.write(newdata)             f.close()         f = open(file_path, "rb")         return f

注意：TextTeaser目前只支持英文摘要。

TextRank

TextRank算法是一种用于文本的基于图的排序算法。其基本思想来源于谷歌的PageRank算法, 通过把文本分割成若干组成单元(单词、句子)并建立图模型, 利用投票机制对文本中的重要成分进行排序, 仅利用单篇文档本身的信息即可实现关键词提取、文摘。和 LDA、HMM 等模型不同, TextRank不需要事先对多篇文档进行学习训练, 因其简洁有效而得到广泛应用。

TextRank 一般模型可以表示为一个有向有权图 G =(V, E), 由点集合 V和边集合 E 组成, E 是V ×V的子集。图中任两点 Vi , Vj 之间边的权重为 wji , 对于一个给定的点 Vi, In(Vi) 为 指 向 该 点 的 点 集 合 , Out(Vi) 为点 Vi 指向的点集合。点 Vi 的得分定义如下:

其中, d 为阻尼系数, 取值范围为 0 到 1, 代表从图中某一特定点指向其他任意点的概率, 一般取值为 0.85。使用TextRank 算法计算图中各点的得分时, 需要给图中的点指定任意的初值, 并递归计算直到收敛, 即图中任意一点的误差率小于给定的极限值时就可以达到收敛, 一般该极限值取 0.0001。

基于TextRank的关键词提取

关键词抽取的任务就是从一段给定的文本中自动抽取出若干有意义的词语或词组。TextRank算法是利用局部词汇之间关系（共现窗口）对后续关键词进行排序，直接从文本本身抽取。其主要步骤如下：

1. 把给定的文本T按照完整句子进行分割，
2. 对于每个句子，进行分词和词性标注处理，并过滤掉停用词，只保留指定词性的单词，如名词、动词、形容词，其中是保留后的候选关键词。
3. 构建候选关键词图G = (V,E)，其中V为节点集，由2生成的候选关键词组成，然后采用共现关系（co-occurrence）构造任两点之间的边，两个节点之间存在边仅当它们对应的词汇在长度为K的窗口中共现，K表示窗口大小，即最多共现K个单词。
4. 根据上面公式，迭代传播各节点的权重，直至收敛。
5. 对节点权重进行倒序排序，从而得到最重要的T个单词，作为候选关键词。
6. 由5得到最重要的T个单词，在原始文本中进行标记，若形成相邻词组，则组合成多词关键词。例如，文本中有句子“Matlab code for plotting ambiguity function”，如果“Matlab”和“code”均属于候选关键词，则组合成“Matlab code”加入关键词序列。

基于TextRank的自动文摘

基于TextRank的自动文摘属于自动摘录，通过选取文本中重要度较高的句子形成文摘，其主要步骤如下：

1. 预处理：将输入的文本或文本集的内容分割成句子得，构建图G =（V,E），其中V为句子集，对句子进行分词、去除停止词，得，其中是保留后的候选关键词。
2. 句子相似度计算：构建图G中的边集E，基于句子间的内容覆盖率，给定两个句子，采用如下公式进行计算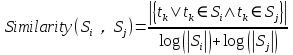：若两个句子之间的相似度大于给定的阈值，就认为这两个句子语义相关并将它们连接起来，即边的权值：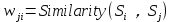
3. 句子权重计算：根据公式，迭代传播权重计算各句子的得分；
4. 抽取文摘句：将3得到的句子得分进行倒序排序，抽取重要度最高的T个句子作为候选文摘句。
5. 形成文摘：根据字数或句子数要求，从候选文摘句中抽取句子组成文摘。

参考资料：

• https://github.com/letiantian/TextRank4ZH
• https://github.com/chenbjin/ASExtractor

玻森自动摘要

玻森采用的是最大边缘相关模型（Maximal Marginal Relevance）的一个变种。MMR是无监督学习模型，它的提出是为了提高信息检索（Information Retrieval）系统的表现。例如搜索引擎就是目前大家最常用的信息检索系统。大家可能经常会碰到，对于我们输入的一个关键词，搜索引擎通常会给出重复的或者内容太接近的检索的情况。为了避免这个现象，搜索引擎可以通过MMR来增加内容的多样性，给出多方面考虑的检索结果，以此来提高表现。这样的思想是可以被借鉴用来做摘要的，因为它是符合摘要的基本要求的，即权衡相关性和多样性。不难理解，摘要结果与原文的相关性越高，它就接近全文中心意思。而考虑多样性则使得摘要内容更加的全面。非常的直观和简单是该模型的一个优点。

相比于其他无监督学习方法，如TextRank（TR）， PageRank（PR）等，MMR是考虑了信息的多样性来避免重复结果。TR，PR是基于图（Graph）的学习方法，每个句子看成点，每两个点之间都有一条带权重（Weighted）的无向边。边的权重隐式定义了不同句子间的游走概率。这些方法把做摘要的问题看成随机游走来找出稳态分布（Stable Distribution）下的高概率（重要）的句子集，但缺点之一便是无法避免选出来的句子相互之间的相似度极高的现象。而MMR方法可以较好地解决句子选择多样性的问题。具体地说，在MMR模型中，同时将相关性和多样性进行衡量。因此，可以方便的调节相关性和多样性的权重来满足偏向“需要相似的内容”或者偏向“需要不同方面的内容”的要求。对于相关性和多样性的具体评估，玻森是通过定义句子之间的语义相似度实现。句子相似度越高，则相关性越高而多样性越低。

自动摘要的核心便是要从原文句子中选一个句子集合，使得该集合在相关性与多样性的评测标准下，得分最高。数学表达式如下：

需要注意的是，D，Q，R，S都为句子集，其中，D表示当前文章，Q表示当前中心意思，R表示当前非摘要，S表示当前摘要。可以看出，在给定句子相似度的情况下，上述MMR的求解为一个标准的最优化问题。但是，上述无监督学习的MMR所得摘要准确性较低，因为全文的结构信息难以被建模，如段落首句应当有更高的权重等。为了提高新闻自动摘要的表现，玻森在模型中加入了全文结构特征，将MMR改为有监督学习方法。从而模型便可以通过训练从“标准摘要”中学习特征以提高准确性。

玻森采用摘要公认的Bi-gram ROUGE F1方法来判断自动生成的摘要和“标准摘要”的接近程度。经过训练，玻森在训练数集上的表现相对于未学习的摘要结果有了明显的提升——训练后的摘要系统F1提高了30%。值得一提的是，在特征训练中，为了改善摘要结果的可读性，玻森加指代关系特征，使得模型表现提高了8%。

相关链接：

• http://bosonnlp.com/
• http://docs.bosonnlp.com/summary.html

其他相关开源项目：

• https://github.com/isnowfy/snownlp
• https://github.com/jannson/yaha
• https://github.com/miso-belica/sumy