复数入门

从入门到入土……

---

复数

先普及基本知识。

众所周知，虚数单位 \(i=\sqrt{-1}\) ，一个复数可以表示为\(a+bi\) ，其中\(a\) 称为实部，\(b\)称为虚部。

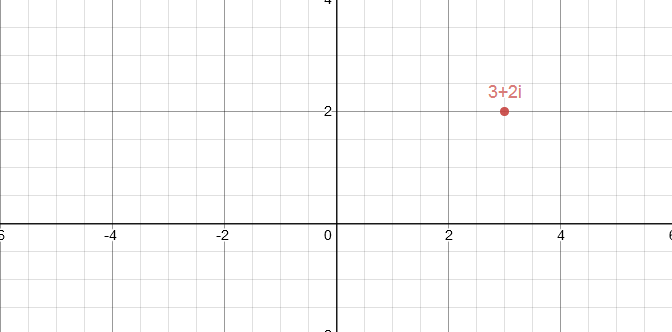
当然，如果把平面直角坐标系的横轴看成实部，纵轴看成虚部，那么它就可以转化成一个点啦！

如图：

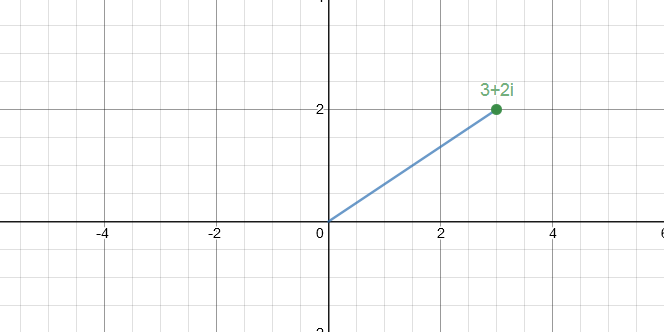
然后以原点为起点，它就变成一个矢量啦！啥啊

如图：

然后看一下复数的四则运算：

加法： \((a+bi)+(c+di)=(a+b)+(c+d)i\)

减法： \((a+bi)-(c+di)*(a-b)+(c-d)i\)
。

乘法： \((a+bi)(c+di)=(ac-bd)+(ad+bc)i\)

除法： \(\dfrac{a+bi}{c+di}=\dfrac{(a+bi)(c-di)}{(c+di)(c-di)}=\dfrac{ac+bd}{c^2+d^2}+\dfrac{(bc-ad)}{c^2+d^2}i\)

接下来引入几个新定义：

幅角 \(\arg z\)：就是它与横轴正半轴的夹角（可正可负）。

对于复数\(a+bi\)，幅角为 \(\arctan \dfrac{b}{a}\) 。

模长：它的长度。

对于复数\(a+bi\)，幅角为 \(\sqrt{a^2+b^2}\) 。

接下来看一下矢量放到坐标系上怎么做四则运算：

加法：随便放到图上就得到平行四边形法则或三角形法则。

减法：大家都知道，一个矢量的负矢量就是和它方向相反，起点相同的矢量。在坐标系上矢量做减法相当于加上它的负矢量。

乘法：模长相乘，幅角相加。

证明：

令两个矢量分别为\(a+bi\)和\(c+di\)。他们的乘积为\((ac-bd)+(ad+bc)i\)。

先证模长相乘。

\[|(a+bi)|\cdot|(c+di)| \]

\[= \sqrt{a^2+b^2} \sqrt{c^2+d^2} \]

\[=\sqrt{a^{2} c^{2} + a^{2} d^{2} + b^{2} c^{2} + b^{2} d^{2}} \]

\[|(ac-bd)+(ad+bc)i| \]

\[=\sqrt{(ac-bd)^2+(ad+bc)^2} \]

\[=\sqrt{a^2c^2+b^2d^2-2abcd+a^2d^2+b^2c^2+2abcd} \]

\[=\sqrt{a^{2} c^{2} + a^{2} d^{2} + b^{2} c^{2} + b^{2} d^{2}} \]

证毕。

再证幅角相加。

众所周知

\[\tan (\alpha+\beta) = \dfrac{\tan \alpha + \tan \beta}{1+ \tan \alpha \tan \beta} \]

\(a+bi\)和\(c+di\)幅角之和的正切值为\(\dfrac{\frac{b}{a}+\frac{d}{c}}{1+\frac{bd}{ac}}=\dfrac{\frac{bc+ad}{ac}}{\frac{ac-bd}{ac}}=\dfrac{bc+ad}{ac-bd}\)

\((ac-bd)+(ad+bc)i\)的幅角的正切值为\(\dfrac{bc+ad}{ac-bd}\)

证毕。

除法：不就乘法的逆运算吗？

---

至此全剧终。

大家可能会很惊讶这有什么用呢？但事实就是他能做FFT，小编也感到非常惊讶。