牛客多校10H Rikka with Ants 【类欧几里得算法】

链接：https://www.nowcoder.com/acm/contest/148/H
来源：牛客网
 

There are two small ants on Rikka's desk. If we consider Rikka's desk as a two-dimensional Cartesian coordinate system, both of them have coordinate (1,0).

Now, Rikka places three obstacles on her desk:
1. y = 0, none of the two ants can walk cross this line.
2. , only the second ant can walk cross this line.
3.  , only the first ant can walk cross this line.

It's remarkable that it is allowed for the ants to stand exactly on the obstacles. For example, if a=b=c=d=1, then both of the ants can reach (1,0),(1,1),(2,1),(2,2) and none of them can reach (1,2),(2,3).

Now, the ants start to move. Their strategy is very simple: In each second, let (x,y) be the current coordinate of one ant, if it can reach (x,y+1), it will walk to this point, otherwise it will walk to (x+1,y).(Since , if the ant can reach (x,y), it can also reach (x+1,y)).

The following image shows the first ant's path when a=3,b=2: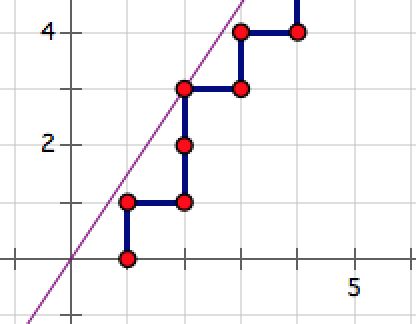


Now, given a,b,c,d, let p1 be the first ant's path and p2 be the second ant's path. Rikka wants you to calculate the number of the points with integer coordinates which are on both p1 and p2.

输入描述:

The first line contains a single integer t(1 ≤ t ≤ 1e5), the number of the testcases.

For each testcase, the first line contains four integers a,b,c,d(1 ≤ a,b,c,d ≤ 1e9).

输出描述:

For each testcase, output a single line with a single number, the answer modulo 998244353. If p1,p2 have infinite many common points, output -1.

题意：在二维坐标系有两条直线和。对于每一条直线，有一只蚂蚁从{1,0}出发，蚂蚁只能向上和向右走且只能沿着整数格点走，并且蚂蚁一直都在直线下方，且蚂蚁必须今贴着直线走。问对于这两条直线的蚂蚁都走过的整数格点的个数。

分析：对于直线蚂蚁走过的整数点为    所以对于两条直线，蚂蚁走过的点为（设）。然后这个点集可以用类欧几里得算法求出来。

#include
using namespace std;
typedef long long LL;
const LL MOD=998244353;
LL mul(LL a,LL b,LL P)
{
    a=(a%P+P)%P,b=(b%P+P)%P;
    return ((a*b-(LL)((long double)a/P*b+1e-6)*P)%P+P)%P;
}
LL f(LL a,LL b,LL c,LL n)
{
    if(a==0)
        return (b/c)*(n+1)%MOD;
    if(a>=c)
        return (n*(n+1)/2%MOD*(a/c)%MOD+f(a%c,b,c,n))%MOD;
    if(b>=c)
        return ((b/c)*(n+1)%MOD+f(a,b%c,c,n))%MOD;
    //LL m=(a*n+b)/c%MOD;
    LL m=(n/c*a+(n%c*a+b)/c);
    return ((m%MOD)*(n%MOD)%MOD-f(c,c-b-1,a,m-1)+MOD)%MOD;
}
int main()
{
    int TA;
    LL a,b,c,d,gc,x,ans;
    scanf("%d",&TA);
    while(TA--)
    {
        scanf("%lld%lld%lld%lld",&a,&b,&c,&d);
        gc=__gcd(a,b);
        a/=gc;b/=gc;
        gc=__gcd(c,d);
        c/=gc;d/=gc;
        if(a==c&&b==d)
        {
            printf("-1\n");
        }
        else
        {
            if(a*d