图信号处理学习笔记（1）：图信号基本知识及其变换

最近在学习图信号处理的相关知识，想进行一些应用层面的实践，恰巧遇到一篇十分具有启发性的推荐算法的论文，故以此文进行简单总结，也作为自己的学习笔记。

Reference:

1. https://en.wikipedia.org/wiki/Laplacian_matrix

一、图信号基本知识

一个无向图 $G$（Graph） 可以定义为：$G=(V,E)$。即无向图由节点集合$V$和边缘集合$E$构成。$V=\{1,2,...,N\}$，$N$为节点个数。部分节点之间存在“连接”（译为links或edges），这些连接集合表示为$E$。具体地，任意不同的两个节点为$i,j\in V$，则$E=\{i,j,w_{ij}\}$，表示节点$i$与节点$j$间的连接权值$w_{ij}$。

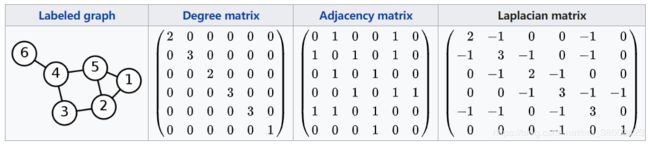
上述的三元组合表达方式并不是非常理想的，我们并不能通过这种表达方式发掘图本身的特征，因此，矩阵被广泛应用于图的表达。基本地，定义邻接矩阵$A$，则一个带有$N$个节点的图可以用大小为$N\ast N$的$A$表示，其中$A(i,j)=w_{ij}$。

除了$A$以外，还有一些常用的矩阵表达方式，分别具有不同的性质，也能够反映不同的图的特征。在此之前，先定义$d_i$为节点$i$的维度，其为节点$i$的所有连接权值的总和。然后，定义维度矩阵$D=diag(d_1,d_2,...,d_N)$，其中$diag()$将向量转变为对角矩阵。

1) Incidence Matrix（关联矩阵）

注：为了方便描述，下述的图都给定为简单图，在简单图中，$A$的元素只由0和1构成。1表示该边存在，反之则为0。如果不是简单图，这些矩阵依然满足下述定义式。

给定无向图$G=(V,E)$，其对应的关联矩阵$\nabla$是一个长宽为$[|E|\ast |V|]$的矩阵。对于矩阵里的每一条边$e=n_i{n}_j$，可以任意给定一个方向。之后，如果节点$x$是边缘$e$的起始节点，则${\nabla }_{ex}=-1$，如果节点$x$是终止节点，则${\nabla }_{ex}=1$。

即，每一行有且仅包含了一个1和一个-1，其余都是0元素。

2) Laplacian Matrix （拉普拉斯矩阵）

Laplacian Matrix可由Incidence Matrix得到：$L={\nabla }^T\nabla$。

同时，若给定一个简单图（simple graph）的邻接矩阵$A$和维度矩阵$D$。则这个图的Laplacian Matrix也可定义为：$$L=D-A$$

上述两式是等价的。具体地，$L$的元素为：
$$L_{i,j}=\{\begin{array}{rlr}{d}_i& & i=j\\ -1& & nodeiisadjacenttoj\\ 0& & otherwise\end{array}$$

拉普拉斯矩阵$L$具有半正定的特性，且各行各列累加都为0。

下面给出半正定的证明： 令${\lambda }_i$和$v_i$为$L$的某一特征值和特征向量对。则有：

$${\lambda }_i=v_i^{T}L{v}_i=v_i^T{\nabla }^T\nabla v_i=(\nabla v_i{)}^T(\nabla v_i)\ge 0$$

所以$L$为半正定矩阵。

3) Symmetric Normalized Laplacian Matrix （对称标准化拉普拉斯矩阵）

一个简单图的对称标准化拉普拉斯矩阵$L^{sym}$定义如下：
$$L^{sym}=D^{-\frac{1}{2}}L{D}^{-\frac{1}{2}}=I-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$$
具体地，$L^{sym}$的元素为：
$$L_{i,j}^{sym}=\{\begin{array}{rlr}1& & i=jand{d}_i̸=0\\ -\frac{1}{\sqrt{d_i{d}_j}}& & nodeiisadjacenttoj\\ 0& & otherwise\end{array}$$
$L^{sym}$在进行了标准化（对角线的值为1）的同时，保留了对称特性。

4）Random Walk Normalized Laplacian （随机游走标准化拉普拉斯矩阵）

随机游走标准化拉普拉斯矩阵$L^{rw}$定义如下：
$$L^{rw}=D^{-1}L=I-D^{-1}A$$
具体地，$L^{rw}$的元素为：
$$L_{i,j}^{rw}=\{\begin{array}{rlr}1& & i=jand{d}_i̸=0\\ -\frac{1}{d_i}& & nodeiisadjacenttoj\\ 0& & otherwise\end{array}$$
$L^{rw}$在进行了标准化的同时，使得每一行的和为0，但失去了对称特性。

4）图信号

以上的三种矩阵表述根据不同的需要，可以十分有力的表达图的结构。但表达的也仅仅是图的结构，就好比是设计好了一栋连接错综复杂的大楼，每一个节点还等着我们去赋值。给定任意一个无向图的邻接矩阵$A$，假定节点数为$N$，则任意的长度为$N$的信号都可以作为这个无向图的图信号，其各个位置的值代表对应节点的值。

二、图信号傅里叶变换（Graph Fourier Transform，GFT）

类比于一维信号的离散时间变换（Discrete Fourier Transform），GFT的变换将图信号线性映射到某一组正交基，但不同于DFT的将不同角频率的三角函数作为正交基，GFT的正交基取决于其Graph的结构，或者更确切地说，是取决于其描述Graph的各种上述提到的矩阵。不过，和DFT类似的是，GFT的目标也是通过线性映射来获取图信号所包含的不同的频率成分。

1) “频率”的定义

对于一个有限长的一维信号，其短时傅里叶变换能够将其分解为不同频率的正弦波的累加和。越高频率的正弦波周期越短，即在短时间内的振荡变化越快。将这个概念衍生到图信号的变换来：节点可以类比于一维信号里时间的概念，对于任意一个节点，与其相连接的节点相比较，如果变化（Variation）剧烈，则可以认为这个节点的频率很高，与瞬时频率比较类似。

定义信号$x$在节点$i$的变化程度$z(i)$，一种很常用的度量方式如下式：
$$z(i)=\sum _{j\in N_i}{w}_{i,j}(x(i)-x(j))$$
其中$N_i$为节点$i$的所有邻接节点。

整个图的变化度量可以定义为上式的加权和：
$$variance=\sum _{i=1}^{N}z(i)x(i)=\sum _{i=1}^N\sum _{j\in N_i}{w}_{i,j}(x(i)-x(j))x(i)$$
不难发现，给定任意一个无向图$G$的拉普拉斯矩阵$L$，上式其实就是$x^{T}Lx$，该式可称为瑞利熵（Rayleigh Quotient）。现在，我们要依次寻找正交基的基向量$u$，来使得$u^{T}Lu$的值可能小。

由于$L$满足各行各列累加都为0，因此下式永远成立：
$$1^{T}L1=0$$
其中$1$为全1列向量。显然，标准化后的$1$向量可以当作这一组正交基的起点向量，表示最低频率成分，记作$u_1=\frac{1}{\sqrt{N}}1$。

由于$L$为半正定，所以对任意向量$v$，必定满足$v^{T}Lv⩾0$。寻找$u_2$，使得$u_2^{T}L{u}_2$最小，并且与$u_1$正交。以此类推，直到找到N个正交向量组成正交基为止。

事实上，这些向量$U=\{u_1,u_2,...,u_N\}$就是$L$的特征向量，并且其特征值从0开始由小到大排列。
$$L=U\Lambda U^T$$

在无向图的前提下，$L$是一个对称矩阵，所以必定能找到标准正交的N个$u$和其对应的特征值。

2) GFT

给定一个无向图，对于任意图信号$x$，其可以由拉普拉斯矩阵的特征向量线性加和构成，加和的系数即为变换后的向量$\tilde{x}$。因此有：
$$x=U\tilde{x}$$
其中$\tilde{x}=U^{T}x$。则$\tilde{x}$中的每一个元素代表了各个频率成分。

3) 可视化

从图中可以看出，当特征值越大，过零点就越多，印证了特征值越大，基向量越高频的性质。