- Markov Decision processes
- Markov Process
- Markov reward process
Markov Decision processes
马尔可夫决策过程,里面有几个术语state,episode,history,value,gain。在后续的学习中,也会有这些术语。
Markov Decision processes 广泛应用于计算机科学和其他工程领域。所以很好的理解它。我们可以分解如下:
- Markov Process(MP).(别名:Markov chain)
- Markov reward Processes.这里扩展了一个
Reward值。 - Mark Decision Processes(MDPs).
Markov Process
这个过程,你只能观察他们的状态。这些状态它们本身有自己的动态变化规则。不为你的意志为转移,我们就只能观察他们。
这些状态的集合,有个名字叫做state space。然后我们随着时间的推移可以获得一个状态链子。(这就是为什么它的别名叫做Markov chain)。举例:中国的南昌市,有晴天和雨天。那么,5天的工作日可能就是[晴天,雨天,雨天,晴天,晴天]。我们观察到就是这个状态链子,我们也称它们为history。
马可夫性质(英语:Markov property),当一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态。啥意思呢?就是今天是晴天,那么明天是晴天还是雨天?依赖于【今天晴天】转为为【明天晴天】和【明天雨天】的概率是多少?
这里我们就可以用一个transition matrix【转移矩阵】来代表上述状态的转移概率。如下表:
| 晴天 | 雨天 | |
|---|---|---|
| 晴天 | 0.8 | 0.2 |
| 雨天 | 0.1 | 0.9 |
这是一个方形矩阵,有i行和j列。那么它的数值表示是state i转移到state j的概率。
什么意思呢?就是如上表,第一行的【晴天】,转移成【明天晴天】的概率是80%,转移成【明天雨天】的概率是20%。第二行的【雨天】,转移成【明天晴天】的概率是10%,转移成【明天雨天】的概率是90%。
所以Markov Process的定义:
- 有一个状态的集合,states(S)
- 有一个转移矩阵,transition matrix(T),代表是转移的概率。
可以看出,我们只能观察上述的变化。没有办法影响他们。【一切都是根据概率随机的变化】
我们给出一个更复杂的例子,来观察他们的状态变化。我们的state space如下:
- 家:家里休息
- 科学研究:去实验室做科学研究
- 喝咖啡:在实验室喝一杯咖啡
- 聊天:和同事针对某个问题讨论,当然,也可能聊闲天。
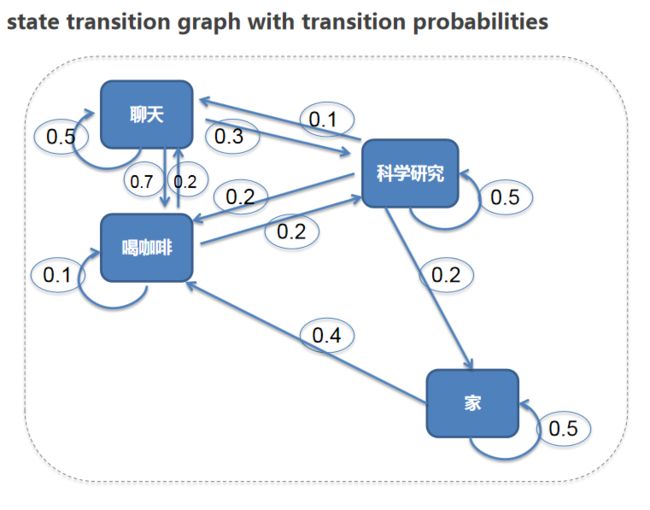
如下图:
我们假定一些规则。例如:你可能从家里去实验室做科研研究,或者去实验室先去喝一杯咖啡再工作。例如,工作遇到问题会去找同事交流沟通等等。那么这些状态变化的概率【概率也是我们自己人为设定的】,我们做一个矩阵。
| 家 | 喝咖啡 | 聊天 | 科学研究 | |
|---|---|---|---|---|
| 家 | 60% | 40% | 0% | 0% |
| 喝咖啡 | 0% | 10% | 70% | 20% |
| 聊天 | 0% | 20% | 50% | 30% |
| 科学研究 | 20% | 20% | 10% | 50% |
这个如果想象成一个真实的时间,每天都会发生不同的经历片段(episodes):
- 家->喝咖啡->聊天->科学研究->家
- 家->喝咖啡->聊天->聊天->科学研究->聊天—>喝咖啡->科学研究->家
- 家->喝咖啡->科学研究->家
我们会发现,每天可能呈现的片段都是不一样的。但是如果你采样的数据足够多,它们的概率分布会是相同的。例如:硬币丢正反。可能10盘里面,70%是正面,30%是反面。但是如果丢10万盘,那么他们的正反面就会无限接近50%的概率。这种概率统计它的魅力也就在于此。
对于RL来说,这种不加手段的自我变化。对于我们来说,是没有很大意义的。为了让他们的变化,接近我们的目标。我们就必须加入reward。来强化它们的行为。那么它就叫做Markov reward process
Markov reward process
可以看到上述图中状态的变化是根据我们设定的概率进行变化的。我们现在给它加个scalar number。
例如:从【家】到【喝咖啡】这个状态变化概率相当于从state i到state j这个状态。我们给与奖励值可以正面的,也可以是负面的。是一个数值。这样就会让他们变化效果更符合我们预期。
除了reward还有一个参数,discount facter γ(gamma)。
上面讨论过,通过观察,我们会获得一个状态链子如:【家->喝咖啡->聊天->科学研究->家】,由于我们给了一个额外的奖励值。所以,对于每一个的episode。我们都可以算出一个这个时间t我们获取的奖励值数量。公式如下:

可以看到,离我们距离越远的时间,我们的γ相乘数越高。例如:0.9的50次方。就是0.005.这个公式,也是为了表现agent的前瞻性。同时,γ的取值在0~1.
这里,由于每一个状态链子都可能不一样,那么获得奖励值数量也会不同。然而,我们可以用数学期望。通过计算一个状态链子的平均值。这个叫做:value of state公式如下:
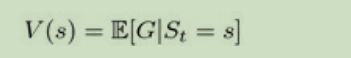
由于理论是空洞难懂的。我们继续举上面那个例子。我们对每一个状态变化设一个奖励值:
- 家->家:得 1 分
- 家->喝咖啡 : 得1分
- 科学研究 ->科学研究 : 得 5 分
- 科学研究 ->聊天: 得 -3 分
- 聊天 -> 科学研究: 得 2 分
- 科学研究 ->喝咖啡 : 得 1 分
- 喝咖啡 ->科学研究 : 得 3 分
- 喝咖啡 ->喝咖啡 : 得 1 分
- 喝咖啡 ->聊天 : 得 2 分
- 聊天 ->喝咖啡 : 得 1 分
- 聊天 ->聊天 : 得 -1 分
未完待续