数据结构——栈
文章目录
- 栈(stack)
- 栈的定义
- 进栈出栈变化形式
- 栈的抽象数据类型
- 栈的顺序存储结构(顺序栈)
- 进栈操作
- 出栈操作
- 两栈共享空间
- 入栈
- 出栈
- 栈的链式存储结构(链栈)
- 进栈操作
- 出栈操作
- 栈的作用
- 栈的应用
- 递归
- 递归的定义
- Fibonacci数列的实现
- Hanoi 塔问题
- 爬楼梯
- 四则运算表达式求值
- 后缀(逆波兰)表示法
- 中缀表达式转后缀表达式
- 计算机处理标准表达式步骤
栈(stack)
栈的定义
- 栈是限定仅在表尾进行插入和删除操作的线性表。
- 栈顶(top) :允许插入和删除的一端。
- 栈底(bottom) :与栈顶相对的一端。
- 空栈:不含任何数据元素的栈。
- 栈又称为先进后出(Last in first out)的线性表,简称 LIFO。
- 栈元素具有线性关系,即前驱和后继关系。
- 进栈,又称为压栈、入栈;
- 出栈,又称为弹栈
进栈出栈变化形式
1、2、3依次进栈,可能的出栈结果:
- 1、2、3进,3、2、1出 => 3、2、1
- 1、2进,2、1出;3进3出 => 2、1、3
- 1进,1出,2进,2出,3进,3出 => 1,2,3
- 1进,1出;2进,3进,3出,2出=> 1, 3, 2
- 1进、2进、2出、3进、3出、1出 => 2,3,1
元素数量越多,其出栈的变化会更多
栈的抽象数据类型
ADT stack
Data
同线性表。元素具有相同的类型,相邻元素具有前驱和后继关系。
Operation
| InitStack(*S) | 初始化操作,建立一个空栈S |
|---|---|
| Destroy(*S) | 若栈存在,则销毁 |
| ClearStack(*S) | 将栈清空 |
| StackEmpty(S) | 若栈为空,则返回true,否则返回false |
| GetTop(S, *e) | 若栈存在且非空,用 e 返回S的栈顶元素 |
| Push(*S, e) | 若栈S存在,插入新元素e到栈S中并成为栈顶元素 |
| Pop(*S, e) | 删除栈S中栈顶元素,并用e返回其值 |
| StackLength(S) | 返回栈S的元素个数 |
endADT
栈的顺序存储结构(顺序栈)
- 下标为 零 的一端作为栈底
- 空栈的判断条件 top = -1
- 栈的结构定义
#define OK 1
#define ERROE 0
#define MAXSIZE 100
typedef struct
{
int data[MAXSIZE];
int top;
}SqStack;
进栈操作
/* 时间复杂度 O(1) */
int Push(SqStack *S, int e)
{
if(S->top == MAXSIZE -1)
return ERROR;
S->data[S->top++] = e;
return OK;
}
出栈操作
/* 时间复杂度 O(1) */
int Pop(SqStack *S, int *e)
{
if(S->top == -1)
return ERROE;
*e = S->data[S->top];
S->top --;
return OK;
}
两栈共享空间
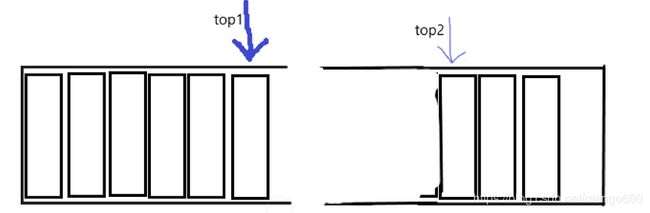
思路: 从数组两端向中间靠拢。top1 和 top2 是栈1 和栈2 的栈顶指针。即只要二者不相碰,则两个栈就可以一直使用。
- top1 = -1,栈1为空
- top2 = n ,栈2为空
- top1 + 1 == top2 时栈满
- 两栈共享空间的结构代码:
typedef struct
{
int data[MAXSIZE];
int top1;
int top2;
}SqDoubleStack;
入栈
在入栈时需要判断给栈1还是栈2插入元素
/* 时间复杂度 O(1) */
int Push(SqDoubleStack *S, int StackNumber, int e)
{
if(S->top1 + 1 == S->top2)
return ERROR;
if(StackNumber == 1)
{
S->data[++S->top1] = e;
}
if(StackNumber == 2)
{
S->data[--S->top2] = e;
}
return OK;
}
出栈
/* 时间复杂度 O(1) */
int Pop(SqDoubleStack *S, int e, int StackNumber)
{
if(StackNumber == 1)
{
if(S->top1 == -1)
return ERROR;
*e = S->data[S->top1--];
}
if(StackNumber == 2)
{
if(S->top2 == MAXSIZE)
return ERROR;
*e = S->data[S->top2++];
}
return OK;
}
栈的链式存储结构(链栈)
- 栈顶放在单链表的头部
- 链栈的结构代码
typedef struct StackNode
{
int data;
struct StackNode *next;
}StackNode, *LinkStackPtr;
typedef struct LinkStack
{
LinkStackPtr top;
int count;
}LinkStack;
进栈操作
/* 时间复杂度 O(1) */
int Push(LinkStack *S, int e)
{
LinkStackPtr s = (LinkStackPtr)malloc(sizeof(StackNode));
s->data = e;
s->next = S->top;
S->top = s;
S->count ++;
return OK;
}
出栈操作
/* 时间复杂度 O(1) */
int Pop(LinkStack *S, int *e)
{
LinkStackPtr p;
if(StackEmpty(*S)) // 判断该链表是否为空
return ERROR;
*e = S->top->data;
p = S->top; // 将栈顶结点赋给p
S->top = S->top->next; // important 栈顶指针下移
free(p);
S->count --;
return OK;
}
如果栈的使用过程中元素变化不可料,有时很小,又是非常大,则选用链栈;如果变化在可控范围内,则选用顺栈。
栈的作用
- 感觉这段话特别棒(来源于大话数据结构)
栈的应用
递归
递归的定义
直接调用自己或通过一席立委的调用语句间接地调用自己的函数,称作递归函数。
每个递归定义必须有一个条件,防止陷入无穷递归
Fibonacci数列的实现
Story time
第一个月的小兔子没有繁殖能力,两个月后,开始生殖
所经过月数 1 2 3 4 5 6 7 8 9 10 11 12 兔子对数 1 1 2 3 5 8 13 21 34 55 89 144 有没有发现这个数列的规律:前两项和等于第三项
/*
* 打印前 40位 Fibonacci 数列
* 迭代法
*/
int main(void)
{
int i;
int a[40];
int a[0] = 0;
int a[1] = 1;
for(i = 2; i <= 40; i ++)
a[i] = a[i-1] + a[i-2];
for(i = 1; i <= 40; i ++)
printf("%d ", a[i]);
return 0;
/*
* 递归法
*/
int Fbi(int i)
{
if(i < 2)
return i == 0 ? 0 :1;
return Fbi(i-1)+Fbi(i-2);
}
int main(void)
{
int i;
for(i = 0; i <= 40; i ++)
printf("%d ", Fbi(i))'
return 0;
}
Hanoi 塔问题
圆盘数 源柱 辅助柱 目标柱
void hanoi(int n, int a, int b, intc)
{
if(n > 0)
{
hanoi(n-1, a, c, b);
move(a, b);
hanoi(n-1, c, b, a);
}
}
爬楼梯
每次走 1 级 或者 2 级,输入楼梯的阶数,求不同的走法?
解决思路:用递归将问题分解成规模更小的子问题
| 阶数 | 走法 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | |
| n-1 | |
| n-2 |
f(n) = f(n-1) + f(n-2)
边界条件:
| n < 0 0 | n=1 1 | n=1 1 |
|---|---|---|
| n = 0 1 | n =0 1 | n=2 2 |
using namespace std;
int N;
int stairs(int n)
{
if(n < 0)
return 0;
if(n == 0)
return 1;
return stairs(n-1) + stairs(n-2);
}
int main()
{
while(cin >> N)
cout << stairs(N) << endl;
return 0;
}
四则运算表达式求值
后缀(逆波兰)表示法
- (Reverse Polish Notation, RPV):不需要括号。
- 举例:
9+(3-1)×3+10÷2
用后缀表达式法为: 9 3 1 - 3*+10 2 / +
- 规则:从左到右遍历表达式中的每个数字和符号,遇到数字就进栈,遇到符号,就将处于栈顶的两个数字出栈,进行运算,运算结果进栈,一直到最终获得结果。
中缀表达式转后缀表达式
- 中缀表达式,即标准四则运算表达式
- 规则:从左到右遍历中缀表达式的每个数字和符号,若是数字就输出,即成为后缀表达式的一部分;若是符号,则判断与栈顶符号的优先级,是右括号或优先级不高于栈顶符号,则栈顶元素依次出栈并输出,并将当前符号进栈,一直到最终输出后缀表达式为止。
计算机处理标准表达式步骤
- 将中缀表达式转化为后缀表达式
- 将后缀表达式进行运算得出结果
