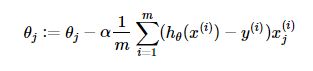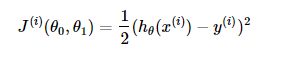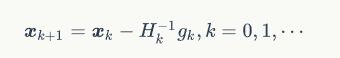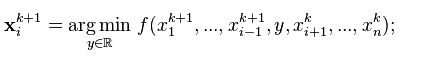最优化算法简单对比 梯度下降 牛顿迭代 坐标下降
梯度下降法、牛顿迭代法和坐标下降法
最优化方法是一种数学方法，它是研究在给定约束之下如何寻求某些因素(的量)，以使某一(或某些)指标达到最优的一些学科的总称。大部分的机器学习算法的本质都是建立优化模型，通过最优化方法对目标函数（或损失函数）进行优化，从而训练出最好的模型。常见的最优化方法有梯度下降法、牛顿法和拟牛顿法、坐标下降法等等。
梯度下降法
梯度下降法是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法。
示例：
只含有一个特征的线性回归，此时线性回归的假设函数是：
其中 i=1,2,...,m表示样本数。
对应的目标函数（代价函数）即为：
下图为 J(θ0+θ1)
与参数θ0和θ1
的关系的图：
1、批量梯度下降（Batch Gradient Descent，BGD）
批量梯度下降法是最原始的形式，它是指在每一次迭代时使用所有样本来进行梯度的更新。从数学上理解如下：
- 对目标函数求偏导：
其中 i=1,2,...,m表示样本数， j=0,表示特征数，这里我们使用了偏置项x0(i)=1
。
- 每次迭代对参数进行更新：
注意这里更新时存在一个求和函数，即为对所有样本进行计算处理，可与下文SGD法进行比较。
伪代码形式为：
其中α
表示学习率，一般根据经验进行设置。
优点：
（1）一次迭代是对所有样本进行计算，此时利用矩阵进行操作，实现了并行。
（2）由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向。当目标函数为凸函数时，BGD一定能够得到全局最优。
缺点：
（1）当样本数目m很大时，每迭代一步都需要对所有样本计算，训练过程会很慢。
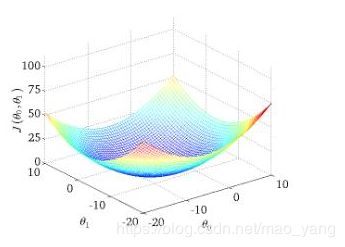
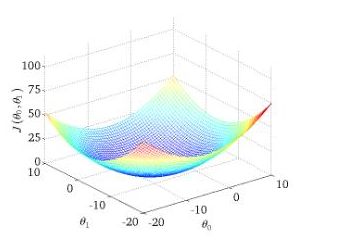
从迭代的次数上来看，BGD迭代的次数相对较少。其迭代的收敛曲线示意图可以表示如下：
2、随机梯度下降（Stochastic Gradient Descent，SGD）
梯度下降法不同于批量梯度下降，随机梯度下降是每次迭代使用一个样本来对参数进行更新。使得训练速度加快。
样本的目标函数为：
- 对目标函数求偏导：
- 参数更新：
注意，这里不再有求和符号 。
伪代码形式为：
优点：
（1）由于不是在全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快。
缺点：
（1）准确度下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛。
（2）可能会收敛到局部最优，由于单个样本并不能代表全体样本的趋势。
（3）不易于并行实现。
3、小批量梯度下降（Mini-Batch Gradient Descent, MBGD）
小批量梯度下降，是对批量梯度下降以及随机梯度下降的一个折中办法。其思想是：每次迭代 使用 ** batch_size** 个样本来对参数进行更新。
这里我们假设batchsize=10 ，样本数 m=1000 。
伪代码形式为：
优点：
（1）通过矩阵运算，每次在一个batch上优化神经网络参数并不会比单个数据慢太多。
（2）每次使用一个batch可以大大减小收敛所需要的迭代次数，同时可以使收敛到的结果更加接近梯度下降的效果。(比如上例中的30W，设置batch_size=100时，需要迭代3000次，远小于SGD的30W次)
（3）可实现并行化。
缺点：
（1）batch_size的不当选择可能会带来一些问题。
batcha_size的选择带来的影响：
（1）在合理地范围内，增大batch_size的好处：
a. 内存利用率提高了，大矩阵乘法的并行化效率提高。
b. 跑完一次 epoch（全数据集）所需的迭代次数减少，对于相同数据量的处理速度进一步加快。
c. 在一定范围内，一般来说 Batch_Size 越大，其确定的下降方向越准，引起训练震荡越小。
（2）盲目增大batch_size的坏处：
a. 内存利用率提高，但是内存容量可能不足。
b. 跑完一次 epoch（全数据集）所需的迭代次数减少，要想达到相同的精度，其所花费的时间大大增加了，从而对参数的修正也就显得更加缓慢。
c. Batch_Size 增大到一定程度，其确定的下降方向已经基本不再变化。
牛顿迭代法
牛顿法的基本思想是利用迭代点
处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似，然后把二次模型的极小点作为新的迭代点，并不断重复这一过程，直至求得满足精度的近似极小值。牛顿法的速度相当快，而且能高度逼近最优值。牛顿法分为基本的牛顿法和全局牛顿法。
- 牛顿法计算函数零点
首先，选择一个接近函数f(x)零点的x0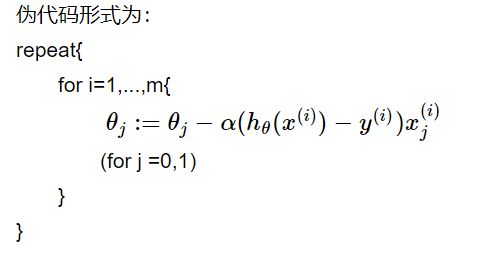，计算相应的f(x0
) 和切线斜率 f'(x0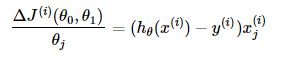)（这里 f'表示函数f的导数）。然后我们计算穿过点 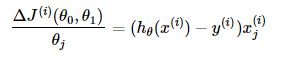(x0,f(x0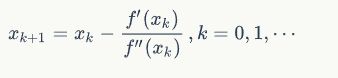
))并且斜率为f'(x0
) 的直线和x轴的交点的x坐标，也就是求如下方程的解：
我们将新求得的点的x坐标命名为x_1，通常 x_1会比x_{0}更接近方程 f(x)=0的解。因此我们现在可以利用x_1开始下一轮迭代。迭代公式可化简为如下所示：
已有证明牛顿迭代法的二次收敛必须满足以下条件：
- f'(x)≠ 0};
- 对于所有x ∈I，其中 I为区间[α − r, α + r]，且x0在区间I内，即 r>=|a-x0|
3、对于所有x ∈I，f''(x)是连续的;
4、x0足够接近根 α。
- 牛顿法求解最优化问题
- 考虑一维的简单情形
简单情形N=1（此时目标函数f(X) 变为f(x) ）.牛顿法的基本思想是：在现有极小点估计值的附近对f(x)做二阶泰勒展开，进而找到极小点的下一个估计值。
设 f(x) 为当前的极小点估计值，则:
表示f(x) 在xk
附近的二阶泰勒展开式（其中略去了关于x-xk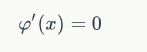
的高阶无穷小项）。
由于求的是最值，由极值必要条件可知， φ(x)应满足：
即：
解得：
于是，若给定初始值x0,则可以构造如下的迭代格式:
产生序列{xk
}来逼近f(x)的极小点。在一定条件下，{xk}可以收敛到f(x)的极小点。
- 对于N>1的情形，二阶泰勒展开式可以做推广，此时:
注意：
1、∇f
和∇2f
中的元素均为关于x的函数，以下分别将其简记为g和H。
2、∇f(xk)和∇2f(xk)表示将x取为xk
后得到的实值向量和矩阵，以下分别将其简记为gk和Hk。
同样地，由于是求极小点，极值必要条件要求它为φ（x）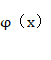
的驻点，即:∇φx=0
对泰勒展开使用梯度算子得:
进一步，若矩阵HK非奇异，则可解得:
于是，若给定初始值x0，则同样可以构造出迭代格式:
这就是原始的牛顿迭代法，其迭代格式中的搜索方向dk=-Hk-1gk称为牛顿方向.
牛顿法的优点：
当目标函数是二次函数时，由于二次泰勒展开函数与原目标函数不是近似而是完全相同的二次式，海森矩阵退化成一个常数矩阵，从任一初始点出发，利用xk+1
的迭代式，只需一步迭代即可达到x的极小点x*，因此牛顿法是一种具有二次收敛性的算法。对于非二次函数，若函数的二次性态较强，或迭代点已进入极小点的领域，则其收敛速度也是很快的，这是牛顿法的主要优点.
牛顿法的缺点：
但原始牛顿法由于迭代公式中没有步长因子，而是定步长迭代，对于非二次目标函数来说，有时会使函数值上升，即出现f(xk+1)>f(xk)的情况，这表明原始牛顿法不能保证函数值稳定地下降.在严重的情况下甚至可能造成迭代点列{xk
}的发散而导致计算失败.
坐标下降法
坐标下降优化方法是一种非梯度优化算法。为了找到一个函数的局部极小值，在每次迭代中可以在当前点处沿一个坐标方向进行一维搜索。在整个过程中循环使用不同的坐标方向。一个周期的一维搜索迭代过程相当于一个梯度迭代。
坐标下降优化方法为了找到一个函数的局部极小值，在每次迭代中可以在当前点处沿一个坐标方向进行一维搜索。在整个过程中循环使用不同的坐标方向。一个周期的一维搜索迭代过程相当于一个梯度迭代。 其实，gradient descent 方法是利用目标函数的导数（梯度）来确定搜索方向的，而该梯度方向可能不与任何坐标轴平行。而coordinate descent方法是利用当前坐标系统进行搜索，不需要求目标函数的导数，只按照某一坐标方向进行搜索最小值。坐标下降法在稀疏矩阵上的计算速度非常快，同时也是Lasso回归最快的解法。
算法描述：
坐标下降法基于的思想是多变量函数可以通过每次沿一个方向优化来获取最小值。与通过梯度获取最速下降的方向不同，在坐标下降法中，优化方向从算法一开始就予以固定。例如，可以选择线性空间的一组基作为搜索方向。 在算法中，循环最小化各个坐标方向上的目标函数值。亦即，如果
已给定，那么，的第个维度为
因而，从一个初始的猜测值
以求得函数
的局部最优值，可以迭代获得的序列。
通过在每一次迭代中采用一维搜索，可以很自然地获得不等式
可以知道，这一序列与最速下降具有类似的收敛性质。如果在某次迭代中，函数得不到优化，说明一个驻点已经达到。
这一过程可以用下图表示。
梯度下降法、牛顿法、和坐标下降法优缺点对比
1、梯度下降法
梯度下降法实现简单，当目标函数是凸函数时，梯度下降法的解是全局解。一般情况下，其解不保证是全局最优解，梯度下降法的速度也未必是最快的。
梯度下降法的优化思想：用当前位置负梯度方向作为搜索方向，因为该方向为当前位置的最快下降方向，所以也被称为是“最速下降法”。最速下降法越接近目标值，步长越小，前进越慢。
缺点：
靠近极小值时收敛速度减慢，求解需要很多次的迭代；
直线搜索时可能会产生一些问题；
可能会“之字形”地下降。
2、牛顿法
牛顿法最大的特点就在于它的收敛速度很快。
优点：二阶收敛，收敛速度快；
缺点：
牛顿法是一种迭代算法，每一步都需要求解目标函数的Hessian矩阵的逆矩阵，计算比较复杂。
牛顿法收敛速度为二阶，对于正定二次函数一步迭代即达最优解。
牛顿法是局部收敛的，当初始点选择不当时，往往导致不收敛；
二阶海塞矩阵必须可逆，否则算法进行困难。
关于牛顿法和梯度下降法的效率对比：
从本质上去看，牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。（牛顿法目光更加长远，所以少走弯路；相对而言，梯度下降法只考虑了局部的最优，没有全局思想。）
3、坐标下降法求最值问题和梯度下降法对比
- 坐标下降法在每次迭代中在当前点处沿一个坐标方向进行一维搜索 ，固定其他的坐标方向，找到一个函数的局部极小值。而梯度下降总是沿着梯度的负方向求函数的局部最小值。
- 坐标下降优化方法是一种非梯度优化算法。在整个过程中依次循环使用不同的坐标方向进行迭代，一个周期的一维搜索迭代过程相当于一个梯度下降的迭代。
- 梯度下降是利用目标函数的导数来确定搜索方向的，该梯度方向可能不与任何坐标轴平行。而坐标下降法法是利用当前坐标方向进行搜索，不需要求目标函数的导数，只按照某一坐标方向进行搜索最小值。
- 两者都是迭代方法，且每一轮迭代，都需要O(mn)的计算量(m为样本数，n为系数向量的维度)
实验效果对比
1、线性问题拟合y = 3*x1 + 4*x2
数据集：代码生成的1000个样本点 X
对比算法：
1、随机梯度下降
2、批量梯度下降
3、小批量梯度下降
对别内容：
1、生成参数
2、算法迭代次数
3、算法运行时间
实验结果：
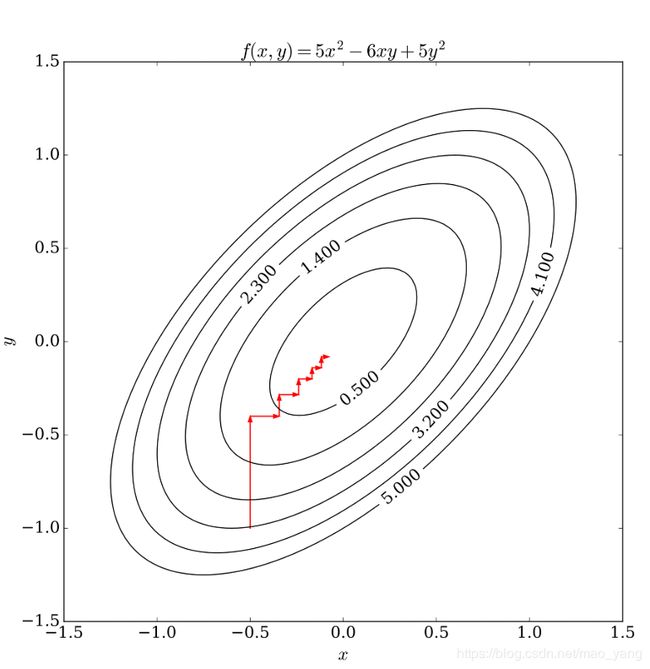
1、非线性问题拟合最优化
已知函数f(x1,x2)=(1 - x1)2 + 100 * (x2 - x12)2
是光滑的凸函数，且只有一个最小值点f(1,1)=0
对比算法：
1、随机梯度下降
2、牛顿法
对别内容：
1、精度损失
2、最优点坐标
3、算法运行时间
实验结果：
代码实现：
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import cm
import numpy as np
import random
import time
def print_Chart():
# fig = plt.figure()
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
# Make data
X = np.linspace(-2, 2, 100)
Y = np.linspace(-2,2, 100)
X, Y = np.meshgrid(X, Y)
Z =(1-X)**2+(X-Y**2)**2*100
# Plot the surface
ax.plot_surface(X, Y, Z, color='g')
plt.show()
def cal_rosenbrock(x1, x2):
"""
计算rosenbrock函数的值
:param x1:
:param x2:
:return:
"""
return (1 - x1) ** 2 + 100 * (x2 - x1 ** 2) ** 2
def cal_rosenbrock_prax(x1, x2):
"""
对x1求偏导
"""
return -2 + 2 * x1 - 400 * (x2 - x1 ** 2) * x1
def cal_rosenbrock_pray(x1, x2):
"""
对x2求偏导
"""
return 200 * (x2 - x1 ** 2)
def gradient_descent(max_iter_count=100000, step_size=0.001,x1=0.0,x2=0.0):
'''
梯度下降
最小值为0
默认初试点(0,0)
:param max_iter_count:
:param step_size:
:param x1:
:param x2:
:return:
'''
pre_x = np.array([x1,x2])
loss = 10
iter_count = 0
while loss > 0.001 and iter_count < max_iter_count:
error = np.zeros((2,), dtype=np.float32)
error[0] = cal_rosenbrock_prax(pre_x[0], pre_x[1])
error[1] = cal_rosenbrock_pray(pre_x[0], pre_x[1])
for j in range(2):
pre_x[j] -= step_size * error[j]
loss = cal_rosenbrock(pre_x[0], pre_x[1]) # 目标值为0
print("iter_count: ", iter_count, "the loss:", loss)
iter_count += 1
return loss,pre_x
def h(x1=0.0,x2=0.0,r=2,c=2):
_h=np.zeros((r,c),dtype=np.float32)
_h[0][0]=2+1200*x1**2-400*x2
_h[0][1]=-400*x1
_h[1][0]=_h[0][1]
_h[1][1]=200
return _h
def g(x1=0.0,x2=0.0):
return np.array([cal_rosenbrock_prax(x1,x2),cal_rosenbrock_pray(x1,x2)])
def newton(max_iter_count=100000,x1=0.0,x2=0.0):
pre_x = np.array([x1,x2])
loss = 10
iter_count = 0
while loss > 0.001 and iter_count < max_iter_count:
h_inv=np.linalg.inv(h(x1=pre_x[0],x2=pre_x[1]))
_g=np.matrix(g(pre_x[0],pre_x[1]).reshape([2,1]))
t=h_inv*_g
for i in range(t.size):
pre_x[i]-=t[i]
loss = cal_rosenbrock(pre_x[0], pre_x[1]) # 目标值为0
print("iter_count: ", iter_count, "the loss:", loss)
iter_count += 1
return loss,pre_x
'''
BGD（批量梯度下降法）
'''
def gen_line_data(sample_num=1000):
"""
y = 3*x1 + 4*x2
:return:
"""
x1 = np.linspace(0, 9, sample_num)
x2 = np.linspace(4, 13, sample_num)
x = np.concatenate(([x1], [x2]), axis=0).T
y = np.dot(x, np.array([3, 4]).T) # y 列向量
return x, y
def bgd(samples, y, step_size=0.01, max_iter_count=10000):
'''
批量梯度下降
:param samples:
:param y:
:param step_size:
:param max_iter_count:
:return:
'''
sample_num, dim = samples.shape
y = y.flatten()
w = np.ones((dim,), dtype=np.float32)
loss = 10
iter_count = 0
while loss > 0.001 and iter_count < max_iter_count:
loss = 0 #每次迭代从新计算受损失值
error = np.zeros((dim,), dtype=np.float32)
'''
遍历所有样本后更新一次参数
'''
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
for j in range(dim):
error[j] += (y[i] - predict_y) * samples[i][j]
for j in range(dim):
w[j] += step_size * error[j] / sample_num
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
error = (1 / (sample_num * dim)) * np.power((predict_y - y[i]), 2)
loss += error
print("iter_count: ", iter_count, "the loss:", loss)
iter_count += 1
return w,iter_count
def mbgd(samples, y, step_size=0.01, max_iter_count=10000, batch_size=0.2):
"""
MBGD（Mini-batch gradient descent）小批量梯度下降：每次迭代使用b组样本
:param samples:
:param y:
:param step_size:
:param max_iter_count:
:param batch_size:
:return:
"""
sample_num, dim = samples.shape
y = y.flatten()
w = np.ones((dim,), dtype=np.float32)
# batch_size = np.ceil(sample_num * batch_size)
loss = 10
iter_count = 0
while loss > 0.001 and iter_count < max_iter_count:
loss = 0
error = np.zeros((dim,), dtype=np.float32)
# batch_samples, batch_y = select_random_samples(samples, y,
# batch_size)
index = random.sample(range(sample_num),
int(np.ceil(sample_num * batch_size)))
batch_samples = samples[index]
batch_y = y[index]
for i in range(len(batch_samples)):
predict_y = np.dot(w.T, batch_samples[i])
for j in range(dim):
error[j] += (batch_y[i] - predict_y) * batch_samples[i][j]
for j in range(dim):
w[j] += step_size * error[j] / sample_num
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
error = (1 / (sample_num * dim)) * np.power((predict_y - y[i]), 2)
loss += error
print("iter_count: ", iter_count, "the loss:", loss)
iter_count += 1
return w,iter_count
def sgd(samples, y, step_size=0.01, max_iter_count=10000):
"""
随机梯度下降法,每读取一次样本后都对参数进行更新
:param samples: 样本
:param y: 结果value
:param step_size: 每一接迭代的步长
:param max_iter_count: 最大的迭代次数
:param batch_size: 随机选取的相对于总样本的大小
:return:
"""
sample_num, dim = samples.shape
y = y.flatten()
w = np.ones((dim,), dtype=np.float32)
loss = 10
iter_count = 0
while loss > 0.001 and iter_count < max_iter_count:
loss = 0
error = np.zeros((dim,), dtype=np.float32)
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
for j in range(dim):
'''
每次读取一个样本后对参数进行更新，
下一个样本使用更新后的参数进行估计
'''
error[j] += (y[i] - predict_y) * samples[i][j]
w[j] += step_size * error[j] / sample_num
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
error = (1 / (sample_num * dim)) * np.power((predict_y - y[i]), 2)
loss += error
print("iter_count: ", iter_count, "the loss:", loss)
iter_count += 1
return w,iter_count
'''
在使用坐标下降算法
对x1求偏导为0时，无法显示的用x2来表示x1
因此该方程不适用于坐标下降算法
'''
# def coordinate_descent(max_iter_count=100000,x1=0.0,x2=0.0):
#
# def cordinate_x1(x1=0.0,x2=0.0):
#
# def cordinate_x1(x1=0.0,x2=0.0):
#
# pre_x = np.array([x1,x2])
# loss = 10
# iter_count = 0
# while loss > 0.001 and iter_count < max_iter_count:
# h_inv=np.linalg.inv(h(x1=pre_x[0],x2=pre_x[1]))
# _g=np.matrix(g(pre_x[0],pre_x[1]).reshape([2,1]))
# t=h_inv*_g
# for i in range(t.size):
# pre_x[i]-=t[i]
# loss = cal_rosenbrock(pre_x[0], pre_x[1]) # 目标值为0
# print("iter_count: ", iter_count, "the loss:", loss)
# iter_count += 1
# return loss,pre_x
if __name__ == '__main__':
# print_Chart()
# 批量梯度下降，线性问题
samples, y = gen_line_data()
time1=time.time()
w1,iter_count1 = bgd(samples, y)
cost_time1=time.time()-time1
print('批量梯度下降结果:',' 参数：',w1,' 迭代次数:',iter_count1,' 使用时间:',cost_time1,'sec')
time2=time.time()
w2,iter_count2=mbgd(samples,y)
cost_time2=time.time()-time2
print('小批量梯度下降结果:',' 参数：',w2,' 迭代次数:',iter_count2,' 使用时间:',cost_time2,'sec')
time3=time.time()
w3,iter_count3=sgd(samples,y)
cost_time3=time.time()-time3
print('=====================运行结果对比===========================')
print('批量梯度下降结果:',' 参数：',w1,' 迭代次数:',iter_count1,' 使用时间:',cost_time1,'sec')
print('小批量梯度下降结果:',' 参数：',w2,' 迭代次数:',iter_count2,' 使用时间:',cost_time2,'sec')
print('随机梯度下降结果:',' 参数：',w3,' 迭代次数:',iter_count3,' 使用时间:',cost_time3,'sec')
'''
非线性问题
'''
# 梯度下降 非线性问题
time4=time.time()
loss,coordinate=gradient_descent(x1=1.5,x2=1.5)
cost_time4=time.time()-time4
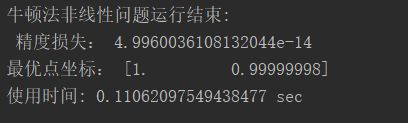
print('随机梯度下降非线性问题运行结束:\n','精度损失:',loss,'\n最优点坐标:',coordinate, '\n使用时间:',cost_time4,'sec')
# 牛顿法 非线性问题
time5=time.time()
loss,pre_x=newton()
cost_time5=time.time()-time4
print('牛顿法非线性问题运行结束:\n','精度损失:',loss,'\n最优点坐标:',pre_x, '\n使用时间:',cost_time5,'sec')