『数据结构』散列表

• 1. 关键字
• 2. 映射
  
  • 2.1. 散列函数 (hash)
    
    • 2.1.1. 简单一致散列
    • 2.1.2. 碰撞 (collision)
    • 2.1.3. str2int 的方法
  • 2.2. 直接寻址法
  • 2.3. 链接法
    
    • 2.3.1. 全域散列 (universal hashing)
      
      • 2.3.1.1. 定义
      • 2.3.1.2. 性质
      • 2.3.1.3. 实现
  • 2.4. 开放寻址法
    
    • 2.4.1. 不成功查找的探查数的期望
      
      • 2.4.1.1. 插入探查数的期望
      • 2.4.1.2. 成功查找的探查数的期望

哈希表 (hash table) , 可以实现 O(1) O ( 1 ) 的 read, write, update
相对应 python 中的 dict, c 语言中的 map

其实数组也能实现, 只是数组用来索引的关键字是下标, 是整数.
而哈希表就是将各种关键字映射到数组下标的一种” 数组”

1. 关键字

由于关键字是用来索引数据的, 所以要求它不能变动 (如果变动, 实际上就是一个新的关键字插入了), 在 python 中表现为 imutable. 常为字符串.

2. 映射

2.1. 散列函数 (hash)

将关键字 k 进行映射, 映射函数 h h , 映射后的数组地址 h(k) h ( k ) .

2.1.1. 简单一致散列

• 简单一致假设: 元素散列到每个链表的可能性是相同的, 且与其他已被散列的元素独立无关.
• 简单一致散列 (simple uniform hashing): 满足简单一致假设的散列

好的散列函数应 满足简单一致假设
例如

(1)h(k)=k mod m(2)h(k)=⌊m(kA mod 1)⌋=kA−⌊kA⌋,\ x(0< A< 1)任何 A 都使用, 最佳的选择与散列的数据特征有关.Knuth 认为, 最理想的是黄金分割数5–√−12≈0.618 ( 1 ) h ( k ) = k   m o d   m ( 2 ) h ( k ) = ⌊ m ( k A   m o d   1 ) ⌋ = k A − ⌊ k A ⌋ ,\ x(0< A< 1) 任何 A 都使用, 最佳的选择与散列的数据特征有关. Knuth 认为, 最理想的是黄金分割数 5 − 1 2 ≈ 0.618

2.1.2. 碰撞 (collision)

由于关键字值域大于映射后的地址值域, 所以可能出现两个关键字有相同的映射地址

2.1.3. str2int 的方法

可以先用 ascii 值, 然后
* 各位相加
* 两位叠加
* 循环移位
* …

2.2. 直接寻址法

将关键字直接对应到数组地址, 即 h(k)=k h ( k ) = k

缺点: 如果关键字值域范围大, 但是数量小, 就会浪费空间, 有可能还不能储存这么大的值域范围.

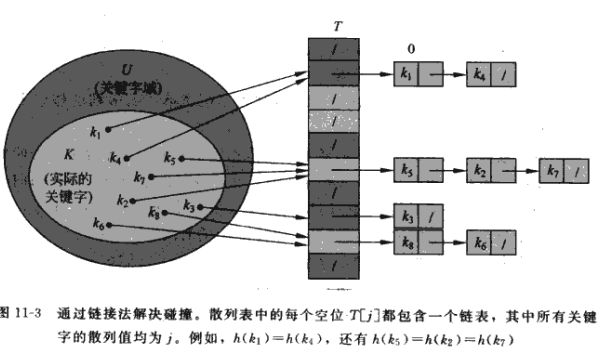
2.3. 链接法

通过链接法来解决碰撞

记有 m 个链表, n 个元素 α=nm α = n m 为每个链表的期望元素个数 (长度)

则查找成功, 或者不成功的时间复杂度为 Θ(1+α) Θ ( 1 + α )
如果 n=O(m),namelyα=O(m)m=O(1) n = O ( m ) , n a m e l y α = O ( m ) m = O ( 1 ) , 则上面的链接法满足 O(1) O ( 1 ) 的速度

2.3.1. 全域散列 (universal hashing)

随机地选择散列函数, 使之独立于要存储的关键字

2.3.1.1. 定义

设一组散列函数 H={h1,h2,…,hi} H = { h 1 , h 2 , … , h i } , 将 关键字域 U 映射到 {0,1,…,m−1} { 0 , 1 , … , m − 1 } , 全域的函数组, 满足

for k≠l ∈U,h(k)=h(l),这样的 h 的个数不超过|H|m f o r   k ≠ l   ∈ U , h ( k ) = h ( l ) , 这样的 h 的个数不超过 | H | m

即从 H 中任选一个散列函数, 当关键字不相等时, 发生碰撞的概率不超过 1m 1 m

2.3.1.2. 性质

对于 m 个槽位的表, 只需 Θ(n) Θ ( n ) 的期望时间来处理 n 个元素的 insert, search, delete, 其中 有 O(m) O ( m ) 个 insert 操作

2.3.1.3. 实现

选择足够大的 prime p, 记 Zp={0,1,…,p−1},Z∗p={1,…,p−1}, Z p = { 0 , 1 , … , p − 1 } , Z p ∗ = { 1 , … , p − 1 } ,
令 ha,b(k)=((ak+b)mod p)mod m h a , b ( k ) = ( ( a k + b ) m o d   p ) m o d   m
则 Hp,m={ha,b|a∈Z∗p,b∈Zp} H p , m = { h a , b | a ∈ Z p ∗ , b ∈ Z p }

2.4. 开放寻址法

所有表项都在散列表中, 没有链表.
且散列表装载因子 α=nm⩽1 α = n m ⩽ 1
这里散列函数再接受一个参数, 作为探测序号
逐一试探 h(k,0),h(k,1),…,h(k,m−1) h ( k , 0 ) , h ( k , 1 ) , … , h ( k , m − 1 ) , 这要有满足的, 就插入, 不再计算后面的 hash 值

探测序列一般分有三种
* 线性  0,1,…,m−1   0 , 1 , … , m − 1
存在一次聚集问题
* 二次  0,1,…,(m−1)2   0 , 1 , … , ( m − 1 ) 2
存在二次聚集问题
* 双重探查
h(k,i)=(h1(k)+i∗h2(k))mod m h ( k , i ) = ( h 1 ( k ) + i ∗ h 2 ( k ) ) m o d   m
为了能查找整个表, 即要为模 m 的完系, 则 h_2(k) 要与 m 互质.
如可以取 h1(k)=k mod m,h2(k)=1+(k mod m−1) h 1 ( k ) = k   m o d   m , h 2 ( k ) = 1 + ( k   m o d   m − 1 )

注意删除时, 不能直接删除掉 (如果有元素插入在其后插入时探测过此地址, 删除后就不能访问到那个元素了), 应该 只是做个标记为删除

2.4.1. 不成功查找的探查数的期望

对于开放寻址散列表, 且 α<1 α < 1 , 一次不成功的查找, 是这样的: 已经装填了 n 个, 总共有 m 个, 则空槽有 m-n 个.
不成功的探查是这样的: 一直探查到已经装填的元素 (但是不是要找的元素), 直到遇到没有装填的空槽. 所以这服从几何分布, 即

p(不成功探查)=p(第一次找到空槽)=m−nm p ( 不成功探查 ) = p ( 第一次找到空槽 ) = m − n m

有

E(探查数)=1p⩽11−α E ( 探查数 ) = 1 p ⩽ 1 1 − α

2.4.1.1. 插入探查数的期望

所以, 插入一个关键字, 也最多需要 11−α 1 1 − α 次, 因为插入过程就是前面都是被占用了的槽, 最后遇到一个空槽. 与探查不成功是一样的过程

2.4.1.2. 成功查找的探查数的期望

成功查找的探查过程与插入是一样的. 所以查找关键字 k 相当于 插入它, 设为第 i+1 个插入的 (前面插入了 i 个, 装载因子 α=im α = i m . 那么期望探查数就是

11−α=11−im=mm−i 1 1 − α = 1 1 − i m = m m − i

则成功查找的期望探查数为

1n∑i=0n−1mm−i=mn∑i=0n−11m−i=mn∑i=m−n+1m1i⩽1α∫mm−n1xdx=1αln11−α 1 n ∑ i = 0 n − 1 m m − i = m n ∑ i = 0 n − 1 1 m − i = m n ∑ i = m − n + 1 m 1 i ⩽ 1 α ∫ m − n m 1 x d x = 1 α l n 1 1 − α

代码

github 地址

class item:
    def __init__(self,key,val,nextItem=None):
        self.key = key
        self.val = val
        self.next = nextItem
    def to(self,it):
        self.next = it
    def __eq__(self,it):
        '''using  keyword  '''
        return self.key == it.key
    def __bool__(self):
        return self.key is not None
    def __str__(self):
        li = []
        nd = self
        while nd:
            li.append(f'({nd.key}:{nd.val})')
            nd = nd.next
        return ' -> '.join(li)
    def __repr__(self):
        return f'item({self.key},{self.val})'
class hashTable:
    def __init__(self,size=100):
        self.size = size
        self.slots=[item(None,None) for i in range(self.size)]
    def __setitem__(self,key,val):
        nd = self.slots[self.myhash(key)]
        while nd.next:
            if nd.key ==key:
                if nd.val!=val: nd.val=val
                return
            nd  = nd.next
        nd.next = item(key,val)

    def myhash(self,key):
        if isinstance(key,str):
            key = sum(ord(i) for i in key)
        if not isinstance(key,int):
            key = hash(key)
        return key % self.size
    def __iter__(self):
        '''when using keyword , such as ' if key in dic',
            the dic's  __iter__ method will be called,(if hasn't, calls __getitem__
            then  ~iterate~  dic's keys to compare whether one equls to the key
        '''
        for nd in self.slots:
            nd = nd.next
            while nd :
                yield nd.key
                nd = nd.next
    def __getitem__(self,key):
        nd =self.slots[ self.myhash(key)].next
        while nd:
            if nd.key==key:
                return nd.val
            nd = nd.next
        raise Exception(f'[KeyError]: {self.__class__.__name__} has no key {key}')

    def __delitem__(self,key):
        '''note that None item and item(None,None) differ with each other,
            which means you should take care of them and correctly cop with None item
            especially when deleting items
        '''
        n = self.myhash(key)
        nd = self.slots[n].next
        if nd.key == key:
            if nd.next is None:
                self.slots[n] =  item(None,None) # be careful
            else:self.slots[n] = nd.next
            return
        while nd:
            if nd.next is None: break  # necessary
            if nd.next.key ==key:
                nd.next = nd.next.next
            nd = nd.next
    def __str__(self):
        li = ['\n\n'+'-'*5+'hashTable'+'-'*5]
        for i,nd in enumerate(self.slots):
            li.append(f'{i}: '+str(nd.next))
        return '\n'.join(li)