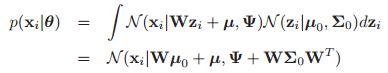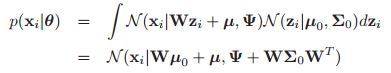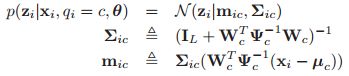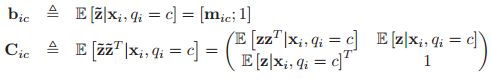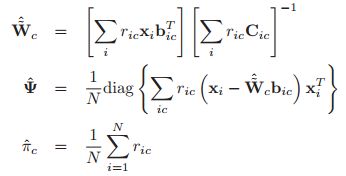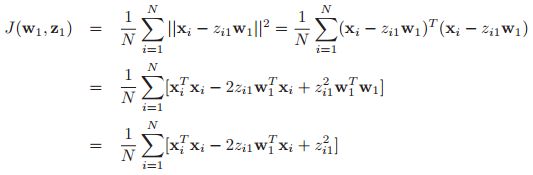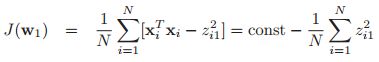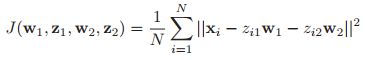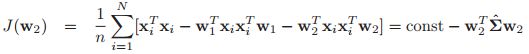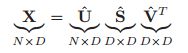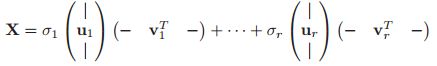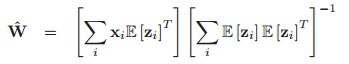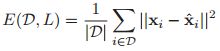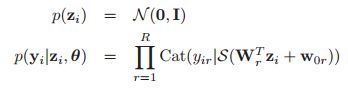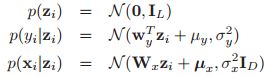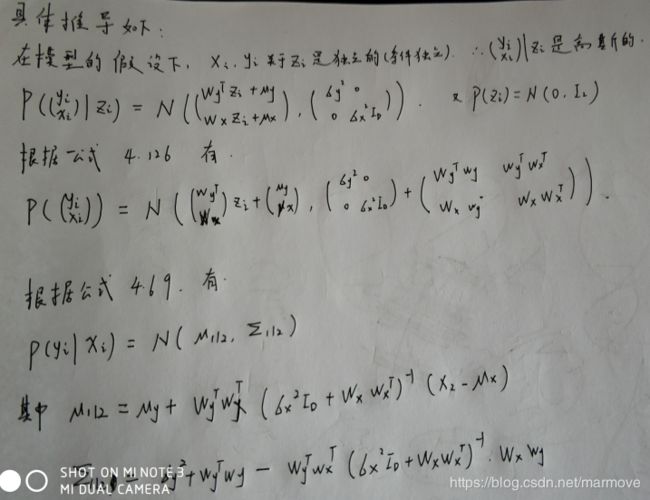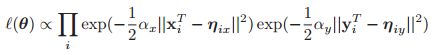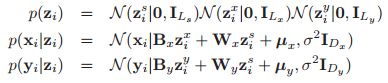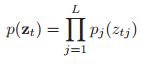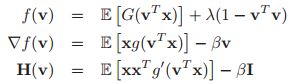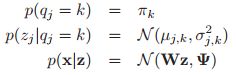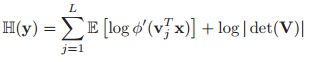MLAPP————第十二章 隐线性模型
第十二章 隐线性模型
12.1 要素分析(factor analysis)
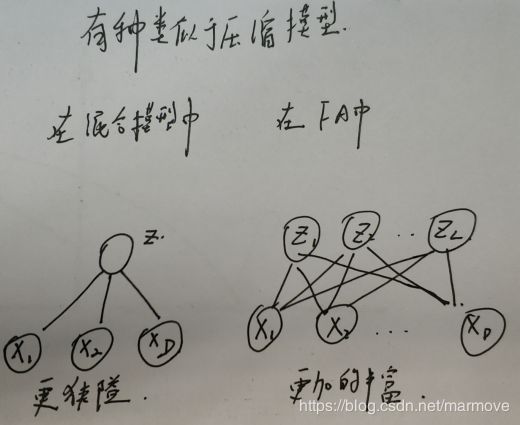
在我们之前提到的混合模型中,数据的生成都是由某个隐状态控制的,然后是那个隐状态控制的分布生成的,但是这样的模型在表示上还是具有一定的局限性,不够完整。
一个可行的方法是引入实值的隐变量![]() ,最简单的先验就是使用高斯的(当然后面也会考虑其它的情况):
,最简单的先验就是使用高斯的(当然后面也会考虑其它的情况):![]() ,如果我们观测到的数据也是连续的话,即:
,如果我们观测到的数据也是连续的话,即:![]() ,那么我们可以假设似然为:
,那么我们可以假设似然为:
![]()
这有点像线性模型一样,不过这里我们做出的假设是均值是关于隐变量的线性模型,这是基于隐变量的条件概率模型(也是似然)。其中![]() 的矩阵,称之为因子载荷矩阵(factor loading matrix),
的矩阵,称之为因子载荷矩阵(factor loading matrix),![]() 是一个
是一个![]() 的协方差矩阵。我们令
的协方差矩阵。我们令![]() 是一个对角阵,因为你想在我们用
是一个对角阵,因为你想在我们用![]() 这个隐变量,某种程度上就是为了简化模型,所以说在
这个隐变量,某种程度上就是为了简化模型,所以说在![]() 已知下,
已知下,![]() 中的任何两个分量是不相关的,也是很合理的。整个模型我们就称之为 factor analysis 或者是FA。一种特殊的情况就是
中的任何两个分量是不相关的,也是很合理的。整个模型我们就称之为 factor analysis 或者是FA。一种特殊的情况就是![]() ,这个称之为概率的主成分分析(probabilistic principle components analysis, PPCA)。
,这个称之为概率的主成分分析(probabilistic principle components analysis, PPCA)。
下图展示了一个简单的例子,其中![]() :
:
关于为什么要用FA,下面是我的一些看法:
12.1.1 FA是MVN的低秩的参数化
FA可以被认为是一种使用少量参数去指定联合密度模型![]() 的方法。我们根据公式4.126,可以得到边缘分布
的方法。我们根据公式4.126,可以得到边缘分布![]() 也是高斯的,并且可以表示为:
也是高斯的,并且可以表示为:
在这里![]() 完全可以耦合到
完全可以耦合到![]() 中去,以及我们也可以令
中去,以及我们也可以令![]() ,即做一个变量代换,所以说不失一般性,我们就可以假设
,即做一个变量代换,所以说不失一般性,我们就可以假设![]() 以及
以及![]() ,所以我们可以发现,这样的话,协方差矩阵就是:
,所以我们可以发现,这样的话,协方差矩阵就是:![]() =
=![]()
因为我们之前说过![]() 是一个对角阵,所以说在这种情况下,我们的参数的个数是
是一个对角阵,所以说在这种情况下,我们的参数的个数是![]() ,但是对于MVN来说,其参数的个数是
,但是对于MVN来说,其参数的个数是![]() ,所以说我们引入隐变量其实是对数据进行了压缩表示,如果我们没有设置
,所以说我们引入隐变量其实是对数据进行了压缩表示,如果我们没有设置![]() 是对角阵,那么这样隐变量的引入就不能减少参数的个数。
是对角阵,那么这样隐变量的引入就不能减少参数的个数。
12.1.2 latent factors的推理
尽管FA可以被看做仅仅是给出了一种关于数据![]() 的一种压缩方法,但是我们总是希望隐变量
的一种压缩方法,但是我们总是希望隐变量![]() 可以揭露数据自身的一些特性。所以我们就想去计算隐变量的后验分布,在高斯的模型下,这个计算是比较简单的,即:
可以揭露数据自身的一些特性。所以我们就想去计算隐变量的后验分布,在高斯的模型下,这个计算是比较简单的,即:
我们可以看到在FA模型中,![]() 其实是独立于i的,所以我们可以用
其实是独立于i的,所以我们可以用![]() 来表示它。计算这个后验协方差矩阵需要
来表示它。计算这个后验协方差矩阵需要![]() ,计算每个
,计算每个![]() 需要
需要![]() ,
,![]() 有时我们称之为latent scores或者是latent factors。
有时我们称之为latent scores或者是latent factors。
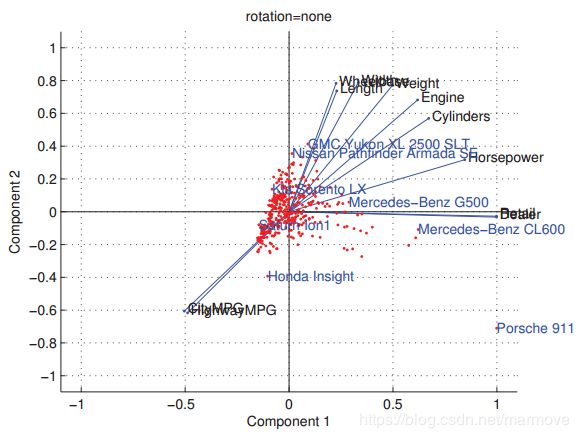
下面我们举一个具体的例子,考虑我们关于汽车的数据集中有![]() 个变量以及有
个变量以及有![]() 组数据。变量包括引擎的尺寸,汽缸的数目,每加仑英里(MPG)以及价格等。我们先拟合一个L=2这样一个模型,那么在这个模型下,我们就可以在平面上画出
组数据。变量包括引擎的尺寸,汽缸的数目,每加仑英里(MPG)以及价格等。我们先拟合一个L=2这样一个模型,那么在这个模型下,我们就可以在平面上画出![]() 的的图,具体如下:
的的图,具体如下:
我们可以看到这上面给了一些不同的车的一些点。(这里我们说明一下为什么叫隐因素,因为在FA中其实可以看成是压缩,但是有时也是一种叫隐藏的因素影响了最终的结果,在这个问题中看似有11的变量,但是实际上有很多是相关的,所以说我们也许用其中的两个或者说我们引入另外两个具有一定物理意义的变量,就可以很好的刻画出最终的结果)
基于上面的解释,我们再来理解一下什么是latent factors。假设我们在做压缩的时候,我们固定的只能是压缩到这11个维度中取两个维度,我们看到上图的蓝线就表示了我们进行这样压缩之后的坐标图的变化情况,在这个例子下,纵坐标表示的是价格,横坐标表示的是MPG。
12.1.3 不唯一性
就像在混合模型中一样,FA这个模型其实也是不唯一的,怎么解释这个事情呢。之前在12.1.1中我们将其实假设![]() 以及
以及![]() 是不失一般性的假设。确实,因为即使你作出了这样的假设只是会使你后面关于
是不失一般性的假设。确实,因为即使你作出了这样的假设只是会使你后面关于![]() 和
和![]() 的估计的结果会不一样。所以在这里我们保持那个假设,那么在这样的假设下,我们发现对于任意的
的估计的结果会不一样。所以在这里我们保持那个假设,那么在这样的假设下,我们发现对于任意的![]() ,只要其满足
,只要其满足![]() ,都会有:
,都会有:
这个分布的结果是一样的结果,均值都是![]() 不变,协方差矩阵
不变,协方差矩阵![]() =
=![]() 。
。
从几何上看这一个现象,我们的![]() 乘以一个正交的矩阵,就是相当于在生成之前把
乘以一个正交的矩阵,就是相当于在生成之前把![]() 进行了旋转,又因为
进行了旋转,又因为![]() 是从一个各向同性的高斯分布中取得的,所以这样对似然就没有什么影响。
是从一个各向同性的高斯分布中取得的,所以这样对似然就没有什么影响。
为了确保我们的解只有一个,我们就需要扔掉![]() 个自由度,因为我们的正交矩阵的维度是
个自由度,因为我们的正交矩阵的维度是![]() 。(怎么来看待这个问题呢,对于一个
。(怎么来看待这个问题呢,对于一个![]() 的正交矩阵来说,它的第一行有L-1个自由的参数,因为长度要为1,第二行则是L-2的自由度,因为要和第一行正交,依次类推)。那么总的来说,在FA模型中,我们的协方差矩阵就只能有
的正交矩阵来说,它的第一行有L-1个自由的参数,因为长度要为1,第二行则是L-2的自由度,因为要和第一行正交,依次类推)。那么总的来说,在FA模型中,我们的协方差矩阵就只能有![]()
![]() 个自由的变量。当然,我们肯定是要求这个值一定是要小于没有被约束的MVN的参数的个数,即
个自由的变量。当然,我们肯定是要求这个值一定是要小于没有被约束的MVN的参数的个数,即![]() ,这就给出了我们进行L选取的一个上界,即:
,这就给出了我们进行L选取的一个上界,即:
![]()
例如,当![]() ,表明
,表明![]() ,当然,我们往往并不会去选择这个上界,因为这样很容易会过拟合(具体关于L的选择参见12.3)。
,当然,我们往往并不会去选择这个上界,因为这样很容易会过拟合(具体关于L的选择参见12.3)。
不幸的是,即使我们选择了![]() ,仍然不能唯一的确定参数,旋转的不确定性仍旧是存在的。尽管这样的一个旋转的特性并不会影响预测的性能,但是它会影响
,仍然不能唯一的确定参数,旋转的不确定性仍旧是存在的。尽管这样的一个旋转的特性并不会影响预测的性能,但是它会影响![]() ,影响了这个就会影响我们关于隐变量的物理解释,这样的话有可能就不能够很好的去揭示模型的相关物理意义。所以说一下还有一些方法:
,影响了这个就会影响我们关于隐变量的物理解释,这样的话有可能就不能够很好的去揭示模型的相关物理意义。所以说一下还有一些方法:
强迫![]() 是标准正交的:对于解不唯一性的最干净的解决办法可能就是强迫
是标准正交的:对于解不唯一性的最干净的解决办法可能就是强迫![]() 是标准正交的,并且列的话按照隐变量的方差从大到小进行降序排列。在12.2中讲的PCA就是用的该种方法。这个方法的解释性也不强,但是至少是唯一的。
是标准正交的,并且列的话按照隐变量的方差从大到小进行降序排列。在12.2中讲的PCA就是用的该种方法。这个方法的解释性也不强,但是至少是唯一的。
强迫![]() 是下三角矩阵:在贝叶斯的体系中,一个非常流行的方法是假设我们的第一个观测到的变量只和第一个隐变量相关,我们的第二个观测到的变量只和第一个和第二个隐变量相关,如此下去。例如当
是下三角矩阵:在贝叶斯的体系中,一个非常流行的方法是假设我们的第一个观测到的变量只和第一个隐变量相关,我们的第二个观测到的变量只和第一个和第二个隐变量相关,如此下去。例如当![]() ,相应的factor loading matrix就是如下形式:
,相应的factor loading matrix就是如下形式:
我们还要求![]() ,在这样的要求下,参数的总共的数目就是
,在这样的要求下,参数的总共的数目就是![]() ,这个和上面说的uniquely的参数数目是一样的。这个方法的缺点就是,前L个观测到的变量是非常重要的,在选取的时候需要十分的谨慎。
,这个和上面说的uniquely的参数数目是一样的。这个方法的缺点就是,前L个观测到的变量是非常重要的,在选取的时候需要十分的谨慎。
增加促使权重稀疏性的先验:我们不去特别的强调![]() 的哪些元素是0,而是去鼓励它的一些元素为0,使用
的哪些元素是0,而是去鼓励它的一些元素为0,使用![]() 正则化,ARD或者spike-and-slab先验(后两种都没听过)。这个叫做稀疏的因素分析,在这个方法下并不强调MAP估计一定是唯一的,但是它鼓励可以解释的一些解。
正则化,ARD或者spike-and-slab先验(后两种都没听过)。这个叫做稀疏的因素分析,在这个方法下并不强调MAP估计一定是唯一的,但是它鼓励可以解释的一些解。
选择有一些信息的旋转矩阵![]() :因为实际上就是
:因为实际上就是![]() 的取值是有很多个,所以我们就想能不能通过一些方法去限制这个
的取值是有很多个,所以我们就想能不能通过一些方法去限制这个![]() ,去增加它的可解释性,经常的,我们就是尽量使
,去增加它的可解释性,经常的,我们就是尽量使![]() 是稀疏的或者近似稀疏的。一个流行的方法就是varimax。
是稀疏的或者近似稀疏的。一个流行的方法就是varimax。
使用非高斯的先验:在后面12.6中我们将会介绍这类方法,叫做ICA。
12.1.4 混合因素分析器(Mixtures of factor analysers)
在FA模型中,我们假设的是我们的数据是在一个低维的线性流形下的。但是实际上在很多应用场合,我们的数据更符合低维的曲线流形这样一个特征。我们可以把曲线的流形近似为一块一块的线性流形的组合。具体的模型如下:
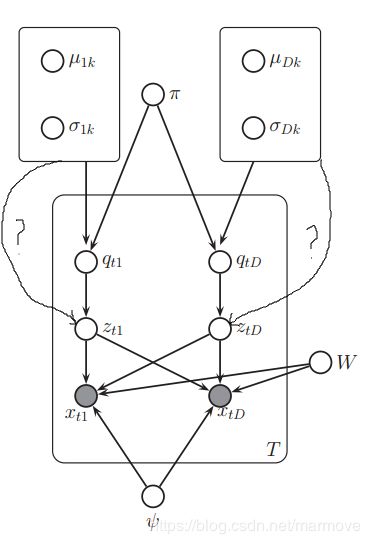
在此模型下,假设我们用K个线性的流形去近似曲线流形,到底选择哪一个线性流形取决于隐变量指示器![]() 。这个模型称之为mixtures of factor analysers(MFA),下图展示了其CI关系:
。这个模型称之为mixtures of factor analysers(MFA),下图展示了其CI关系:
另一个方法去看待这个模型,就是把它看成低秩的混合高斯模型。实际上,这个模型只需要![]() 个参数,而不是GMM中
个参数,而不是GMM中![]() ,过多的参数容易导致过拟合。事实上MFA对于高维的实数据是一个非常好的压缩模型。
,过多的参数容易导致过拟合。事实上MFA对于高维的实数据是一个非常好的压缩模型。
12.1.5 EM算法应用到FA模型中
直接使用第四章的一些推导结果,我们可以很直接的将EM算法应用到FA模型中去,并且只需要一些微小的变动就可以运用到MFA中去。书上说下面只会给出一些直接的结果,并不会给出相关的证明,我们来看一看,如果可以的话,也是可以简单的证明一下。
下面给出的是MFA的结果,对于FA来说,就是设定![]() 。
。
在E step中,我们有:
![]()
下面证明一下为什么是这样
关于![]() 的条件后验是:
的条件后验是:
这一点的证明可以由4.4得到。
在M step中,同时去估计![]() 是最简单的,定义
是最简单的,定义![]()
![]() ,
,![]() ,同时定义:
,同时定义:
M step的结果如下:
在(Zhao 和 Yu 2008)这篇文章中提出了更加快速的EM算法,基于ECM(并不太懂)。
12.1.6 FA模型有missing data的拟合
在很多的应用场合中,比如说协同过滤,我们总会有一些缺失的数据。当然在11章中,我们已经讲过怎么处理missing data,其实就是做相关的期望就可以了,所以其实并不是很难。但是呢,如果missing data太多了,就可能会导致过拟合的情况,那么这个时候使用MAP估计或者是贝叶斯推理可能就会显得比较有用(Ilin and Raiko 2010)。
12.2 主成份分析(Principal components analysis, PCA)
考虑在FA模型中,如果我们限制![]() ,并且
,并且![]() 是正交的。在(Tipping and Bishop 1999)中,当
是正交的。在(Tipping and Bishop 1999)中,当![]() ,模型就变成了经典的(非概率下的)主成份分析方法(PCA),也称作Karhunen Loeve变形。当
,模型就变成了经典的(非概率下的)主成份分析方法(PCA),也称作Karhunen Loeve变形。当![]() ,就称之为概率模型下的PCA(PPCA)(Tipping and Bishop 1999),或者叫做sensible PCA(Roweis 1997)。
,就称之为概率模型下的PCA(PPCA)(Tipping and Bishop 1999),或者叫做sensible PCA(Roweis 1997)。
我们下面就会从这两个方面去进行讲解。
12.2.1 经典的PCA:定理的陈述
定理12.2.1:首先我们有一组数据![]() 是D维的,总共有N个,我们希望找到一个矩阵
是D维的,总共有N个,我们希望找到一个矩阵![]() 是LxD维度的,其中
是LxD维度的,其中![]() 的列与列之间是正交的,那么通过这个我们就可以对数据
的列与列之间是正交的,那么通过这个我们就可以对数据![]() 进行压缩,即
进行压缩,即![]() ,那么我们的目标就是使得:
,那么我们的目标就是使得:
最小,其中![]() (这里要证明在重构矩阵是
(这里要证明在重构矩阵是![]() 的情况下,压缩矩阵是
的情况下,压缩矩阵是![]() 是最好的。),当然我们也可以写成矩阵的形式,即:
是最好的。),当然我们也可以写成矩阵的形式,即:
其中![]() ,
,![]() 是一个DxL的矩阵。那么我们怎么选择这个
是一个DxL的矩阵。那么我们怎么选择这个![]() 才能够使得这个重构误差最小呢,我们的方法就是计算矩阵
才能够使得这个重构误差最小呢,我们的方法就是计算矩阵![]() (为了表示的简单,这里假设
(为了表示的简单,这里假设![]() 要不然还要加上一项)的前L个大的特征值对应的特征向量作为
要不然还要加上一项)的前L个大的特征值对应的特征向量作为![]() 的L个列,即
的L个列,即![]() 。
。
下图左边就是一个D=2,L=1的例子:
我们可以清楚地看到,所有的点都投影到了这条直线上,这里就找了一个最主要的主成份。
对于高维的情况,我们很难像上面这张图进行可视化,但是在图像中,我们还是可以去这么做,把每一幅图看做一个数据,然后去做分析,通过图像的重构的样子来进行分析,具体如下(b是针对某一幅图的重构形状):
下面我们将会说明,在PCA中,最主要的那个方向其实就是方差最大的那个方向。这就意味着,主成份分析的方法可能会由于数据本身的测量尺度差异导致的某些方差大的方向被认为是主方向,但是实际上并不是这样的。所以在进行PCA处理之前,我们要对数据进行标准化,所以其实我们计算的是相关矩阵而不是协方差矩阵。
12.2.2 证明*
证明:我们使用![]() 去表明第j个主方向,
去表明第j个主方向,![]() 表明第i个高维的观测数据,
表明第i个高维的观测数据,![]() 表明的是对应于第i个观测数据的压缩表示,
表明的是对应于第i个观测数据的压缩表示,![]() 表明的是所有N个低维向量的第j个元素。
表明的是所有N个低维向量的第j个元素。
首先,我们先来找第一个主分量![]() ,以及相应的投影向量
,以及相应的投影向量![]() ,接着我们会去找第二个以及第三个
,接着我们会去找第二个以及第三个![]() 等。重构误差具体可以写成如下的形式:
等。重构误差具体可以写成如下的形式:
这里由于标准正交性假设,所以![]() 。首先我们对
。首先我们对![]() 进行求导,并令最后的结果为0,即:
进行求导,并令最后的结果为0,即:
这一点告诉我们如果我们的重构矩阵是![]() 意味着,我们的压缩矩阵必然是
意味着,我们的压缩矩阵必然是![]() ,这样才会使得重构误差最小。有了这样一个前提,那么我们的目标函数就变成了只跟
,这样才会使得重构误差最小。有了这样一个前提,那么我们的目标函数就变成了只跟![]() 有关了:
有关了:
其实我们后面有![]() const
const![]()
![]() ,从这个式子本身看的话,它是一个二次的,还是一个凹函数,那么求最小值,利用梯度的方法肯定是不行的,所以需要从另一个观点来看这个问题。
,从这个式子本身看的话,它是一个二次的,还是一个凹函数,那么求最小值,利用梯度的方法肯定是不行的,所以需要从另一个观点来看这个问题。
我们有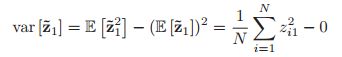 ,这里要注意这个
,这里要注意这个![]() 并非上面的向量,而是指一个随机变量,指被压缩的第一个元素的随机变量。那么因为我们上面在讲述定理的时候提到过就是为了简单起见,所以假设均值是0的,这样我们就有
并非上面的向量,而是指一个随机变量,指被压缩的第一个元素的随机变量。那么因为我们上面在讲述定理的时候提到过就是为了简单起见,所以假设均值是0的,这样我们就有![]() ,书上这里的符号写的一团糟,这里
,书上这里的符号写的一团糟,这里![]() 与
与![]() 都是表示压缩的那个随机变量,
都是表示压缩的那个随机变量,![]() 则是表示观测到数据的随机变量。所以我们看到,最小化重构误差其实就等价于最小化压缩数据的方差,即:
则是表示观测到数据的随机变量。所以我们看到,最小化重构误差其实就等价于最小化压缩数据的方差,即:![]() 。这就是之前我们为什么总说PCA喜欢找方差大的那个方向。
。这就是之前我们为什么总说PCA喜欢找方差大的那个方向。
投影数据的方差可以写为: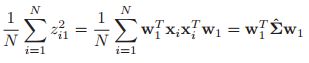 ,其中
,其中![]() 是经验协方差矩阵(从采样的角度来看的)。
是经验协方差矩阵(从采样的角度来看的)。
因为直接优化![]() 其实是不可能的,我们刚才也看到了,因为
其实是不可能的,我们刚才也看到了,因为![]() 趋向于无穷就会无穷小,所以在做优化是利用带约束的优化,利用拉格朗日乘子法,即优化:
趋向于无穷就会无穷小,所以在做优化是利用带约束的优化,利用拉格朗日乘子法,即优化:
令导数为0,即![]() ,得到
,得到![]() ,吧这个带入到原始的式子,很显然,我们就是要找一个最大的
,吧这个带入到原始的式子,很显然,我们就是要找一个最大的![]() ,那么我们的
,那么我们的![]() 又是
又是![]() 的特征值,所以其必然就是最大的特征值,所以
的特征值,所以其必然就是最大的特征值,所以![]() 就是最大特征值对应的特征变量。
就是最大特征值对应的特征变量。
下面我们就来找另一个方向进一步最小化重构概率,其中![]() 以及
以及![]() 。那么重构误差就是:
。那么重构误差就是:
关于![]() 和
和![]() 的优化结果和之前一样,那么关于
的优化结果和之前一样,那么关于![]() 式子的结果是
式子的结果是![]() ,这个是很容易求的,所以同样的,我们可以得到
,这个是很容易求的,所以同样的,我们可以得到
利用与上面相同的方法,求导,带入,我们可以得到:![]() ,所以是第二个最大的特征值。对于更大的L证明也是同样如此。
,所以是第二个最大的特征值。对于更大的L证明也是同样如此。
12.2.3 奇异值分解(SVD)
我们上一节中已经通过协方差矩阵的特征值定义了PCA的解,我们是通过求导,利用拉格朗日的方法进行的求解。然而基于奇异值分解,我们还有另一种方法 (其实我的第一反应就是奇异值分解)。
对于一个实的![]() 的矩阵
的矩阵![]() ,奇异值分解的定义如下:
,奇异值分解的定义如下:
其中![]() 是一个
是一个![]() 矩阵,行和列都是标准正交的,即
矩阵,行和列都是标准正交的,即![]() =
=![]() ,而
,而![]() 是一个
是一个![]() 的矩阵,同样有
的矩阵,同样有![]() ,
,![]() 是
是![]() ,只有对角线上有元素,有
,只有对角线上有元素,有![]() 奇异值
奇异值![]() 。可以看下面的示意图:
。可以看下面的示意图:
因为如上图的阴影部分所示,最后N-D列其实计算结果是等于0,所以可以cut掉,这个就叫做经济的SVD,省去了一些不需要计算的量,如果N>D,即为:
相反,如果![]() ,即为:
,即为:
特征值和奇异向量之间的关系是,对于任意一个实向量![]() ,其奇异值分解是
,其奇异值分解是![]() ,我们有:
,我们有:
![]()
其中![]() (对角为奇异值的平方)。因此我们有:
(对角为奇异值的平方)。因此我们有:
![]()
所以![]() 的特征向量就是
的特征向量就是![]() 的右奇异向量。对应的特征值就是奇异值的平方。相似的:
的右奇异向量。对应的特征值就是奇异值的平方。相似的:
特征向量就是左奇异向量,特征值也是奇异值的平方。总体来说就是:
![]()
所以根据上面的规则,我们很容易就可以得到![]() 的特征值和特征向量。
的特征值和特征向量。
另外我们还可以进一步进行理解,其实我们的![]() 还可以分解成如下的形式:
还可以分解成如下的形式:
如果奇异值所占的分量很小,那么我们就可以做如下的近似:
![]()
这个称之为截断的SVD,即:
在这样的情况下,我们表达一个![]() 的矩阵就只需要
的矩阵就只需要![]() 这么些参数就好。
这么些参数就好。
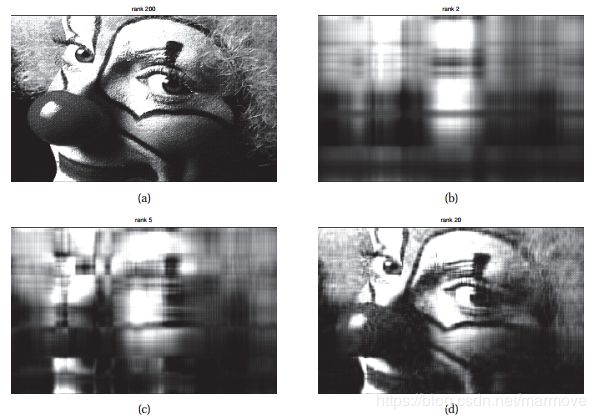
考虑一个具体的例子,下图中左上角的图是一个![]() 像素点的图像:
像素点的图像:
总共我们有![]() 个参数,但是右下角的由于取得是L=20,所以只用了
个参数,但是右下角的由于取得是L=20,所以只用了![]() 就能够比较好的表示出来。
就能够比较好的表示出来。
其实我们的误差近似就等于:
![]()
有人证明了这个方法是最好的把矩阵近似成秩为L的最好方法。
我们再次回到PCA,如果我们对![]() 进行截断的SVD,即
进行截断的SVD,即![]() ,那么我们的
,那么我们的![]() ,以及
,以及![]() ,所以
,所以![]() ,那么我们重构的
,那么我们重构的![]() ,即
,即![]() ,这与我们用截断的SVD是一样的。这也从另一个方面解释了PCA为什么要选这样的
,这与我们用截断的SVD是一样的。这也从另一个方面解释了PCA为什么要选这样的![]() (特征向量)。
(特征向量)。
12.2.4 概率模型的PCA
现在我们来看看PPCA是一个什么样的情况。
定理 12.2.2 我们考虑在FA模型中![]() ,并且
,并且![]() 是标准正交的。那么观测到的数据的对数似然就是(这里为了公式的简洁,假设数据是0均值的)(书上写错了,少了个括号):
是标准正交的。那么观测到的数据的对数似然就是(这里为了公式的简洁,假设数据是0均值的)(书上写错了,少了个括号):
其中![]() ,
,![]() ,
,![]() ,并记
,并记![]() =
= ![]() 。那么最大似然的结果就是:
。那么最大似然的结果就是:![]() ,其中
,其中![]() 是任意的标准正交阵,
是任意的标准正交阵,![]() 是
是![]() 的矩阵,是
的矩阵,是![]() 的前L个特征向量。
的前L个特征向量。![]() 是前L个特征值构成的对角阵。不失一般性,我们可以设定
是前L个特征值构成的对角阵。不失一般性,我们可以设定![]() ,进一步我们可以得到噪声的方差的估计值,就是扔掉的特征值的平均,其物理意义就是扔掉的那些维度的噪声方差的平均:
,进一步我们可以得到噪声的方差的估计值,就是扔掉的特征值的平均,其物理意义就是扔掉的那些维度的噪声方差的平均:
书上说当![]() ,我们有
,我们有![]() ,PPCA就是PCA,但是从结果的式子里我看不出来,这一点我觉得可能是在计算过程中才能体现,所以这一点目前还是有很多疑惑。关于隐变量的后验分布具体如下:
,PPCA就是PCA,但是从结果的式子里我看不出来,这一点我觉得可能是在计算过程中才能体现,所以这一点目前还是有很多疑惑。关于隐变量的后验分布具体如下:
这一点根据12.1.5的EM分析可以得到。因此当![]() ,我们有
,我们有![]() ,这就是经典的PCA。
,这就是经典的PCA。
12.2.5 EM算法在PCA上的应用
下面我们将EM算法应用在PCA上,即![]() 的概率模型上。令
的概率模型上。令![]() 是一个
是一个![]() 的矩阵,存储N个后验均值的。
的矩阵,存储N个后验均值的。![]() 的每一列存储了原始的数据。那么根据公式12.63,我们有
的每一列存储了原始的数据。那么根据公式12.63,我们有![]() ,这对应的就是E step,因为
,这对应的就是E step,因为![]() ,所以是delta分布。在M step中,我们有:
,所以是delta分布。在M step中,我们有:
这是根据式子12.63得到的,去掉了![]() ,并且方差的计算公式(cov(x) = E(x^2)-E(x)^2),以及我们有
,并且方差的计算公式(cov(x) = E(x^2)-E(x)^2),以及我们有![]() 。这个式子的结果和多输出的线性回归(公式7.89
。这个式子的结果和多输出的线性回归(公式7.89![]() )的结果具有非常强的相似性,其实仔细一想这PCA和多输出的线性回归确实有很强的相似性。
)的结果具有非常强的相似性,其实仔细一想这PCA和多输出的线性回归确实有很强的相似性。
总的来说,对于PCA,我们的EM算法的过程就是:
Bishop1999表明在这个背景下,EM算法唯一的稳定的固定点就是全局最优解。所以EM算法必然收敛到的解![]() ,就是前L个特征向量张成的空间的解。当然我们需要对其进行标准正交化,同时我们也能将其修整为基的方向(即特征向量对应的方向)。
,就是前L个特征向量张成的空间的解。当然我们需要对其进行标准正交化,同时我们也能将其修整为基的方向(即特征向量对应的方向)。
那么我们之前说可以通过特征值分解很好的进行PCA,为什么还要用EM算法呢,其必然有一些优势:
1.EM算法算的更快。假设![]() ,那么EM算法的计算复杂度主要集中在E step中,为
,那么EM算法的计算复杂度主要集中在E step中,为![]() ,T是迭代的次数,在实验的方法中T往往是比较小的,即使N,D很大。而特征值分解则是
,T是迭代的次数,在实验的方法中T往往是比较小的,即使N,D很大。而特征值分解则是![]() ,相比EM算法,这个的复杂度肯定是更高的。
,相比EM算法,这个的复杂度肯定是更高的。
2.EM算法可以运用到在线学习中(这一点实现起来很简单,只要把数据不停的更新就好了)。
3.EM算法可以很好的解决missing data(因为在概率的背景下,我们总是可以通过边缘分布把未知的给积分掉)。
4.EM算法可硬应用到混合PPCA或者FA模型中。
5.EM可以改进成为variational EM或者是variational Bayes EM来拟合更加复杂的模型。
12.3 选择隐藏的维度的数目(压缩到几维的)
前面讨论怎么选择混合模型的K,不过好像并没有给出很好的方法,只是讨论了一下可能用哪些方法。在这一节当中,我们要讨论怎么选择FA/PCA的隐维度。
12.3.1 FA/PPCA的模型选择
这里的叙述与11.5十分的相似,在贝叶斯的框架下,理论上,进行模型的选择就是计算![]() ,但是实际上还是有两个问题。第一个就是计算LVMs的边际似然太难了。实际上一些简单的方法,例如BIC或者变分的lower bound会被用来近似这个。或者我们可以用CV的方法,但是CV的方法就是太慢了。
,但是实际上还是有两个问题。第一个就是计算LVMs的边际似然太难了。实际上一些简单的方法,例如BIC或者变分的lower bound会被用来近似这个。或者我们可以用CV的方法,但是CV的方法就是太慢了。
第二个问题就是我们要去把很大的一个L的集合,去一个一个算,哪一个是最大的。那么常用的方法就是穷举(慢)。或者说,我们选一个我们认为最大的了L,然后去砍,这在后面13.7中会讲一个方法叫做automatic relevancy determination(ARD)结合EM算法,可以自动的去修剪出不相关的一些权重。关于这个技术在13章中会应用到监督学习的背景下。在Bishop的书中,讲了怎么应用到FA中。
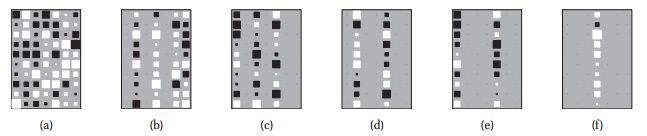
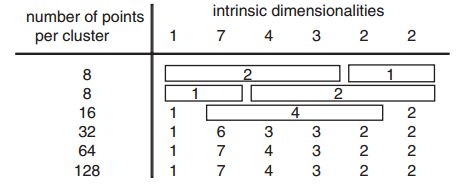
我们看下图:
L从7(L=D),变成了4,3,2,2,1。
数据越少的时候,模型会倾向于往简单的方向发展,当数据逐渐变多的时候,这个时候会往正确的方向收敛。如下表所示
尽管ARD/EM方法是比较优雅的,但是它仍需要去不停的serch,通过“birth”或者“death”的方法进行操作。另外一种方法就是基于随机采样的方法(这一块等学了后面再来思考)。
12.3.2 关于PCA的模型的选择
针对PCA模型,其实我们就是要最小化重构误差:
之前我们的PCA都是假设观测数据是0均值的,对于非0均值的PCA具体如下:![]() ,
,![]() ,
,![]() 都可以从训练数据中获得。这里
都可以从训练数据中获得。这里![]() =
= ![]() ,
, ,
,![]() 可以根据奇异值分解求得。
可以根据奇异值分解求得。
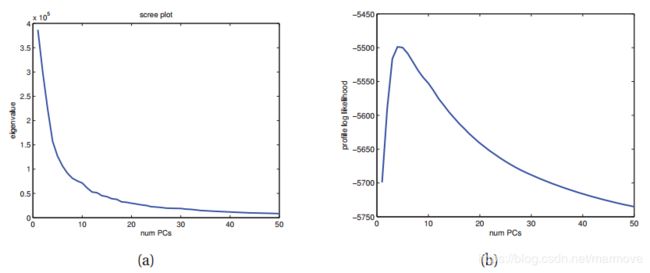
下图是MNIST数据的![]() 曲线:
曲线:
我们可以看到曲线下降的非常快,这就意味着其实我们并不需要太大的L就能很好的表示数据。
我们可以得到:
具体的证明如下:
所以其实画这个曲线就是计算以降序排列最小的那些被扔掉的特征值的和就好了。
另一个我们用来衡量这个误差的量叫做解释方差分数(fraction of variance explained),定义如下:
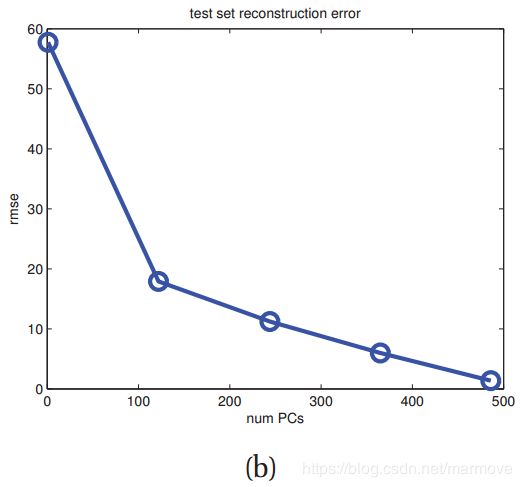
当然,对于训练数据而言,如果我们使用![]() ,就没有重构误差了,但是这会导致过拟合,所以我们其实是要在测试集上看性能比较好,具体如下:
,就没有重构误差了,但是这会导致过拟合,所以我们其实是要在测试集上看性能比较好,具体如下:
但是我们发现,我们并没有得到我们想得到的那种U形的曲线。
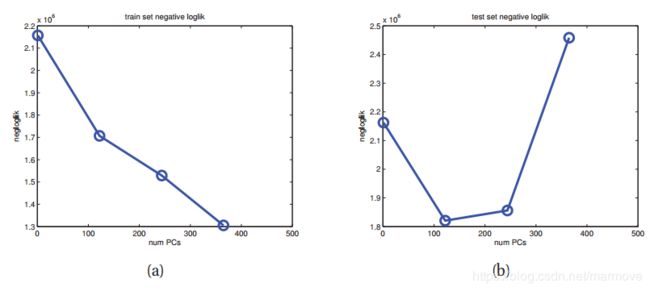
这其实解释起来也很简单,因为我们在做PCA的时候,其实并不是计算数据的model,其实是在压缩数据,如果你的维度很高,但是大量的数据都是0,也是可以没有误差的完美的压缩数据,所以从这个角度看,PCA就是你的维度越大越好,我压缩的就越接近真实的数据,这无论对于测试集还是训练集都是一样的。相反,在贝叶斯框架下就不一样,贝叶斯奥卡姆准则表明,如果你的数据量只有一点点的话,那么更复杂的模型是会收到punish的。在下图中我们可以明显的看出:
这个在训练集的时候就可以很明显的看出是呈现U字型的,在11.5.2中,我们也曾类似的提到过这一点,对于K-means算法和GMM算法,GMM算法是呈现U字型的,这就是概率模型的好处,在贝叶斯的框架下,可以很好的避免过拟合。
12.3.2.1 Profile likelyhood
尽管我们的error随着L的变化不是呈现U型的,但是有可能出现类似拐点的东西,即误差突然从一个很大的值变到一个很小的值。在Zhu and Ghodsi 2006里面提到了一个与之相关的算法。在PCA里面关于误差的衡量其实就是与特征值![]() 有关的,这在之前我们已经证明过了,其中
有关的,这在之前我们已经证明过了,其中![]() ,该思想同样也可以应用到K-means算法中,但是不是特征值了。讲这些值分成两个部分,取决于
,该思想同样也可以应用到K-means算法中,但是不是特征值了。讲这些值分成两个部分,取决于![]() ,其中
,其中![]() 是我们后面要决定的阈值。为了计算L,我们使用一个简单的变更点模型(没遇到过),即令当
是我们后面要决定的阈值。为了计算L,我们使用一个简单的变更点模型(没遇到过),即令当![]() ,有
,有![]() ,当
,当![]() ,有
,有![]() (这里假设两个部分的方差是一样的,是防止模型由于数据分布的不均匀导致的模型过拟合)。我们假设在每个部分里,我们的
(这里假设两个部分的方差是一样的,是防止模型由于数据分布的不均匀导致的模型过拟合)。我们假设在每个部分里,我们的![]() 是独立同分布的,虽然这样不是很合理,但是计算上会很简单。对于不同的L,我们都可以计算相应的似然函数,具体如下:
是独立同分布的,虽然这样不是很合理,但是计算上会很简单。对于不同的L,我们都可以计算相应的似然函数,具体如下:
这个就称之为profile log likelihood,其中我们有:
最终,我们选择![]() ,下图展示了这样的一个过程:
,下图展示了这样的一个过程:
我们可以看到,在这个方法下,我们就有最优点了。
12.4 PCA在分类数据上的应用
在这一节中,我们讲FA模型推广到观察的数据是离散数据的情况(分类问题)。那么我们的数据是![]() ,其中
,其中![]() 是我们观测到的数据的维度。我们假设
是我们观测到的数据的维度。我们假设![]() 是由隐变量
是由隐变量![]() 生成的,并且该隐变量具有高斯先验,具体的概率模型如下:
生成的,并且该隐变量具有高斯先验,具体的概率模型如下:
其中![]() ,
,![]() ,
,![]() (这里的M是不是就应该等于C)(这里书上说必须加上这一个偏移项,要是让
(这里的M是不是就应该等于C)(这里书上说必须加上这一个偏移项,要是让![]() 里面的一个元素为1的话,计算后验方差的话会有问题)。与FA分析的一样,我们假设先验的参数
里面的一个元素为1的话,计算后验方差的话会有问题)。与FA分析的一样,我们假设先验的参数![]() ,
,![]() ,因为这些参数可以被耦合到
,因为这些参数可以被耦合到![]() 以及
以及![]() 中,我们称这样的模型为categorical PCA,在27章中,我们将讨论与之相关的模型。当我们去改变模型的参数的时候,我们的模型就可能会变成各种各样很复杂的模型,这会非常的有趣。
中,我们称这样的模型为categorical PCA,在27章中,我们将讨论与之相关的模型。当我们去改变模型的参数的时候,我们的模型就可能会变成各种各样很复杂的模型,这会非常的有趣。
那么我们怎么去拟合这个模型呢,我们使用一个modifiedEM算法,在Estep中,我们用一个高斯分布去近似![]() ,然后在Mstep中去计算
,然后在Mstep中去计算![]() ,关于多分类的模型,具体可以参见Khan et al. 2010。在21章中,我们也会更加详细的去介绍,并有相关的习题。
,关于多分类的模型,具体可以参见Khan et al. 2010。在21章中,我们也会更加详细的去介绍,并有相关的习题。
12.5 PCA算法应用到成对的或者是多视角的数据
在现实生活中,我们将常会遇到数据集是有多个相关信息的数据的。比如说:基因表达和基因拷贝数,或者说是电影的用户评分以及用户评论。很自然的,我们想把这些数据结合到一起。这就是数据融合的一个例子。有些时候我们希望根据其中的一个数据,来估计数据对里面的另一个数据(利用低维融合的数据)。
下面我们将具体聊一聊关于隐高斯模型的相关例子,相关的资料是(Virtanen 2010),我们的数据对是![]() ,其中
,其中![]() 。关于其他一些离散的模型,我们将在27章中进行叙述。
。关于其他一些离散的模型,我们将在27章中进行叙述。
12.5.1 监督PCA(隐因素回归)
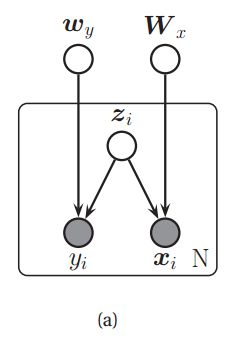
考虑如下的模型:
其概率图模型如下:
在这个模型中,我们可以得到![]() 的分布,具体的推导如下:
的分布,具体的推导如下:
书上会进行进一步的稍微的简化,但是结果上基本没有区别,只是符号上替换了一下:![]() ,其中我们有
,其中我们有![]() 。
。
我们假设我们的先验是Zellner s g-prior,即![]() ,会有一些很有趣的联系。首先我们对
,会有一些很有趣的联系。首先我们对![]() (每一行对应一个数据)进行奇异值分解:
(每一行对应一个数据)进行奇异值分解:![]() ,其中
,其中![]() ,那么在(West 2003)中有
,那么在(West 2003)中有![]() ,这个
,这个![]() 是12.78里面的
是12.78里面的![]() 。
。
上面我们都是讨论的回归的模型。在(Guo 2009)中将CCA(chechik 2005)推广到指数家族,这将更加的适用于如果![]() 和\或
和\或![]() 是离散数据下的情况。尽管在这样的模型下,我们不能计算
是离散数据下的情况。尽管在这样的模型下,我们不能计算![]() 的闭式表达式,但是其实与回归模型相似,我们还是用隐变量这个瓶颈去解决问题。
的闭式表达式,但是其实与回归模型相似,我们还是用隐变量这个瓶颈去解决问题。
我们将利用信息论的知识去压缩![]() 来估计
来估计![]() 。事实上,我们需要找一个编码分布
。事实上,我们需要找一个编码分布![]() 来最小化:
来最小化:![]() ,其中
,其中![]() 是用来控制压缩率和估计精度的一个折中参数。
是用来控制压缩率和估计精度的一个折中参数。
12.5.1.1 判决监督PCA
关于上面的模型的一个问题就是在进行输入估计和输出估计的时候,权重系数是一样的。所以为了使得模型更加的合理,我们定义如下的目标函数:
其中![]() 控制着数据源的权重,以及
控制着数据源的权重,以及![]() 。对于高斯数据,我们看到
。对于高斯数据,我们看到![]() 仅仅控制着噪声的方差:
仅仅控制着噪声的方差:
这种解释更适用于指数族。但是请注意,参数![]() 很难估计,因为改变他们会改变归一化的常数。下面我们给出另一种方法使得
很难估计,因为改变他们会改变归一化的常数。下面我们给出另一种方法使得![]() 的权重更重一点。
的权重更重一点。
12.5.2 偏最小二乘法
一个叫做偏最小二乘的方法(partial least squares,PLS)是非对称的监督PCA。具体的思想如下:
就是不共享隐变量,输入有自己的隐变量。具体的概率图模型如下:
那么联合概率分布就是:
其中![]() 以及:
以及:
在这里,共同子空间的L要相对比较大。
12.5.3 典范相关分析
典范相关分析(canonical correlation analysis,CCA)与我们之前提到的PLS有点像,区别就在于,这个模型允许我们的输入和输出都有自己私有的子空间,以及公共的子空间,也就是我们有三个隐变量:![]() (公有的),
(公有的),![]() (输入的)
(输入的)![]() (输出的)。我们的模型如下:
(输出的)。我们的模型如下:
具体的图模型如下:
相应的观测联合分布是:
其中![]() ,同时我们有:
,同时我们有:
有人使用EM算法计算这个的MLE表明MLE的结果和传统的非概率模型是一样的。但是在概率模型下我们有很多的优点:我们可以将M拓展到大于2的情况,就是有好几类数据,不仅是两类;我们可以建立混合的CCA模型;我么可以使用ARD建立稀疏的版本;我们可以推广到指数家族;我们可以对参数使用贝叶斯推理的方法;我们可以加一些先验;具体的看书上的推荐文章,暂时我还没有这么深入研究的打算,23333。
12.6 独立成分分析(ICA)
考虑下面的情况。假设你在一个非常拥挤的房间,房间里很多人都在讲话。你的耳朵实际上就像两个麦克风,它们在听房间里不同语音信号的线性组合。您的目标是将混合信号分解为它们对应的组成部分。这就是鸡尾酒会上的问题,也是盲信号分离(BSS)或盲源分离的一个例子,盲意味着我们对信号的来源一无所知。除了在声信号处理方面的明显应用外,在分析脑电图和脑磁图信号、财务数据和任何其他潜在源或因素以线性方式混合在一起的数据集(不一定是时间数据集)时,也会出现这个问题。
下面我们将对模型进行定义。![]() 是在t时刻的观测信号,
是在t时刻的观测信号,![]() 代表的是源信号。我们假设:
代表的是源信号。我们假设:![]() ,其中
,其中![]() 是一个
是一个![]() 的矩阵,并且
的矩阵,并且![]() ,在这一节中,每一个时间的数据都是相互独立的,我们不建立时间相关模型(所以我们可以用i替换t下标,但是我们坚持用t,为了和其它ICA文献保持一致)。那我们的目的就是去推理源信号
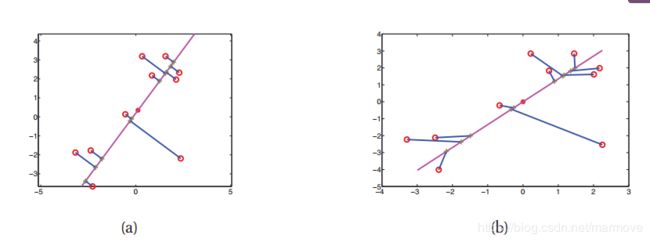
,在这一节中,每一个时间的数据都是相互独立的,我们不建立时间相关模型(所以我们可以用i替换t下标,但是我们坚持用t,为了和其它ICA文献保持一致)。那我们的目的就是去推理源信号![]() ,下图就是一个具体的例子:
,下图就是一个具体的例子:
在我们的背景里,![]() 被称作混合矩阵,如果L=D,意味着,我们的传感器的数目与源的数目相等,
被称作混合矩阵,如果L=D,意味着,我们的传感器的数目与源的数目相等,![]() 就是方阵,为了简单,我们假设噪声水平是0(不明白噪声水平是0是什么意思)。
就是方阵,为了简单,我们假设噪声水平是0(不明白噪声水平是0是什么意思)。
目前看来,这个模型和FA模型好像没什么区别(PCA就是对应于没有噪声,除了我们没有要求![]() 是标准正交的)。但是我们在这里会用一个不一样的先验
是标准正交的)。但是我们在这里会用一个不一样的先验![]() ,在PCA里面,我们假设每一个源都是独立的,其先验都是高斯的:
,在PCA里面,我们假设每一个源都是独立的,其先验都是高斯的:
现在我们假设我们的源分布可以是任意的非高斯的分布:
不失一般性,我们可以将源分布的方差约束为1,因为任何其他方差都可以通过适当地缩放![]() 进行建模。得到的模型称为独立成分分析(independent component analysis, ICA)。
进行建模。得到的模型称为独立成分分析(independent component analysis, ICA)。
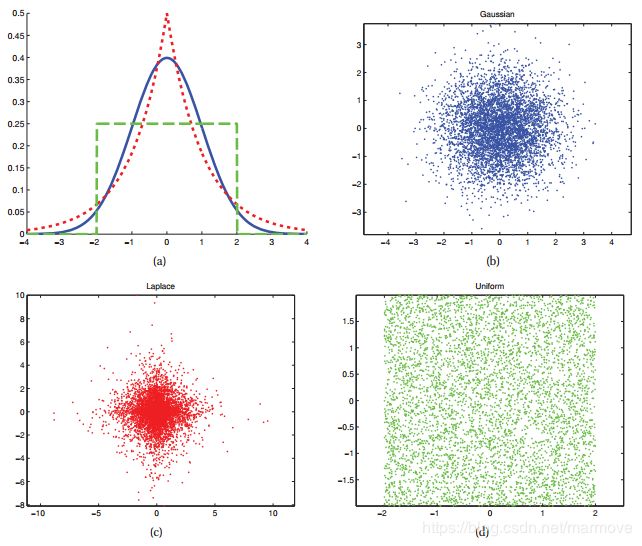
高斯分布在ICA中不作为先验源的原因是它不允许源的唯一恢复,具体我们参照上图的图(c)可以很明显的看到。这是因为PCA似然对于源![]() 和混合矩阵
和混合矩阵![]() 的任何正交变换都是不变的,PCA可以恢复信号所在的最佳线性子空间,但不能唯一地恢复信号本身。
的任何正交变换都是不变的,PCA可以恢复信号所在的最佳线性子空间,但不能唯一地恢复信号本身。
因此在PCA下,我们缺乏一个旋转信息,所以我们能估计出子空间,但是不能唯一确定模型,但是ICA可以。但是呢ICA需要![]() 是一个方阵,这样它才可逆,如果不是方阵的化,我们也不能唯一的恢复出最终的结果,但是我们可以去计算出后验
是一个方阵,这样它才可逆,如果不是方阵的化,我们也不能唯一的恢复出最终的结果,但是我们可以去计算出后验![]() 。当然不管对于哪一种情况,我们都需要去估计
。当然不管对于哪一种情况,我们都需要去估计![]() 以及源的分布
以及源的分布![]() 。
。
12.6.1 最大似然估计
这一节中,我们讨论的模型是方阵的混合矩阵![]() 以及没有噪声的ICA模型。和之前一样,我们还是可以假设我们的观测是零均值的,因此我们同样可以假设
以及没有噪声的ICA模型。和之前一样,我们还是可以假设我们的观测是零均值的,因此我们同样可以假设![]() 也是0均值的。另外,我们假设观测被白化了,关于白化,我在网上找了这么一段解释,感觉还可以:
也是0均值的。另外,我们假设观测被白化了,关于白化,我在网上找了这么一段解释,感觉还可以:
所以被白化的数据,必然有![]() ,同时我们根据无噪,同时
,同时我们根据无噪,同时![]() 是独立0均值,方差为1的分布,又可以得到:
是独立0均值,方差为1的分布,又可以得到:
所以我们说![]() 必须是标准正交的。这样我们估计的参数就从
必须是标准正交的。这样我们估计的参数就从![]() 减少到了
减少到了![]() ,这样就简化了算法和计算。
,这样就简化了算法和计算。
令![]() ,其中
,其中![]() 称作recognition weights,
称作recognition weights,![]() 称作generative weights。
称作generative weights。
因为![]() ,根据公式2.89,我们有:
,根据公式2.89,我们有:
![]()
那么我们T个独立同分布数据的log似然函数就是:
其中![]() 是
是![]() 的第j行。因为我们知道
的第j行。因为我们知道![]() 是标准正交的,所以式子最左边第一项是可以扔掉的(是个常数),那么我们的NLL就可以写成如下的形式(争对所有可能的数据,写成期望的形式):
是标准正交的,所以式子最左边第一项是可以扔掉的(是个常数),那么我们的NLL就可以写成如下的形式(争对所有可能的数据,写成期望的形式):
其中![]() 。我们希望在以
。我们希望在以![]() 为标准正交的前提下,最小化NLL。
为标准正交的前提下,最小化NLL。
关于这个的求解可以用梯度法,牛顿法,或者是EM算法。不同的算法各有各的优势,相比能用EM,肯定是EM更好。
12.6.2 FastICA 算法
在这一节中将一个fast ICA算法,在这里我们只讲利用近似的牛顿法解ICA问题,主要是基于(Hyvarinen and Oja 2000)。
为了简单起见,我们假设我们的隐变量只有一个,并且我们假设我们的源的分布是已知的并且是一样的(这里只有一个隐变量不就意味着我们的源只有一个吗)。因此![]() ,令
,令![]() ,那么目标函数以及其梯度和汉森矩阵如下:
,那么目标函数以及其梯度和汉森矩阵如下:
其中![]() ,我们做如下的近似:
,我们做如下的近似:
![]()
![]() (这里少乘了一个I),做了这样的近似,汉森矩阵就是一个常数乘以单位阵,所以我们的牛顿step如下:
(这里少乘了一个I),做了这样的近似,汉森矩阵就是一个常数乘以单位阵,所以我们的牛顿step如下:
书上说也可以写为![]() ,但是我发现前面的公式推不到后面这个公式(在实践中,期望可以被训练集的蒙特卡洛估计所取代,这提供了一个有效的在线学习算法)。执行此更新之后,应该使用以下公式将
,但是我发现前面的公式推不到后面这个公式(在实践中,期望可以被训练集的蒙特卡洛估计所取代,这提供了一个有效的在线学习算法)。执行此更新之后,应该使用以下公式将![]() 投射回约束表面:
投射回约束表面:![]() 。我们不停的迭代,算法就会收敛,但是这里的
。我们不停的迭代,算法就会收敛,但是这里的![]() 可能并不一定会收敛,但是
可能并不一定会收敛,但是![]() 会收敛于1。我们可以顺序的学习
会收敛于1。我们可以顺序的学习![]() ,并把当前学习的
,并把当前学习的![]() 在之前的子空间中投影的部分给去掉,我们也可以并行的去学习
在之前的子空间中投影的部分给去掉,我们也可以并行的去学习![]() 。后面这个可能会更常用,因为不像PCA,这里的特征并没有什么顺序,所以用相同的处理方式处理它们可能会更好。
。后面这个可能会更常用,因为不像PCA,这里的特征并没有什么顺序,所以用相同的处理方式处理它们可能会更好。
12.6.2.1 对源密度的建模
上一节中,我们都是假设![]() 是已知的,那么什么样的先验适合做我们模型的先验呢?我们知道使用高斯分布是没有用的,所以我们需要一些非高斯的分布。一般来说,有几种非高斯分布,如下所示:
是已知的,那么什么样的先验适合做我们模型的先验呢?我们知道使用高斯分布是没有用的,所以我们需要一些非高斯的分布。一般来说,有几种非高斯分布,如下所示:
超高斯分布:这类分布在均值处有一个很大的尖,然后有一个很重重的尾巴。拉普拉斯分布就是一个简单的例子,如下图:
我们称一个分布是超高斯的或者是leptokurtic,如果其![]() ,其中
,其中![]() 是分布的峰度,其定义如下:
是分布的峰度,其定义如下:
![]() ,其中
,其中![]() 是标准差,
是标准差,![]() 是k阶中心矩,具体计算公式是
是k阶中心矩,具体计算公式是![]() ,通常在峰度的定义中要减去3,使高斯变量的峰度等于零。
,通常在峰度的定义中要减去3,使高斯变量的峰度等于零。
次高斯分布:这类分布的峰度是负的,这些分布比高斯分布平坦得多,均匀分布是一个典型的例子。
偏态分布:另一种非高斯的方法是不对称。衡量这一点的一个指标是偏斜度,定义如下:![]() ,偏斜分布的一个具体的例子就是gamma分布。
,偏斜分布的一个具体的例子就是gamma分布。
当我们观察许多自然信号的经验分布时,例如图像和语音,当通过某些线性滤波器时,它们往往是超高斯的。因此,用ICA建模自然信号的一个明显的选择是拉普拉斯分布。对于0均值和方差为1的拉普拉斯分布,我们有:![]() 。因为拉普拉斯先验在原点是不可微的,所以更常用其他平滑的超高斯分布。另一个例子就是logistic分布,相应的0均值和方差为1(
。因为拉普拉斯先验在原点是不可微的,所以更常用其他平滑的超高斯分布。另一个例子就是logistic分布,相应的0均值和方差为1(![]() 以及
以及![]() )的分布的log为:
)的分布的log为:![]() 。(Pham and Garrat 1997)中有很多关于
。(Pham and Garrat 1997)中有很多关于![]() 估计的方法。然而,当用最大似然拟合ICA时,知道源分布的确切形状并不重要(但是还是要知道是超高斯的或者是次高斯的)。因此对于超高斯的,我们往往用
估计的方法。然而,当用最大似然拟合ICA时,知道源分布的确切形状并不重要(但是还是要知道是超高斯的或者是次高斯的)。因此对于超高斯的,我们往往用![]() ,次高斯的用
,次高斯的用![]() ,而不会用其他的更复杂的表达式。
,而不会用其他的更复杂的表达式。
12.6.3 使用EM算法(这一块暂时还没有看懂,整个估计过程是怎么样的)
这里就是说了,对于![]() ,我们不是不知道这个分布是什么样的吗,前面讲了一些模型,那么我们还可以用一些比较灵活的分布,比如GMM,那么这样的化,模型就变成这样:
,我们不是不知道这个分布是什么样的吗,前面讲了一些模型,那么我们还可以用一些比较灵活的分布,比如GMM,那么这样的化,模型就变成这样:
概率图如下:
对于该模型,我们可以用EM算法来做。我们可以通过穷举的办法去计算![]() (不过这样会很浪费时间,有利用变分方法做的)
(不过这样会很浪费时间,有利用变分方法做的)
12.6.4 其他的估计原则*
很多时候我们会看到一些方法不是用最大似然估计来求ICA模型的参数。下面我们会介绍这些方法,这些方法会给出一些更深的见解,但是最终我们都会发现,这些算法和最大似然其实是没有区别的。
12.6.4.1 Maximizing non-Gaussianity
一个比较早的方法,就是找一个矩阵![]() ,使得分布
,使得分布![]() 离高斯分布越远越好。之前我们讲过测量非高性的一个函数是
离高斯分布越远越好。之前我们讲过测量非高性的一个函数是![]() ,但是这个对于异常值非常的敏感。另一个测量方法是negentropy(负熵),定义如下:
,但是这个对于异常值非常的敏感。另一个测量方法是negentropy(负熵),定义如下:![]() ,其中:
,其中:![]() 。因为高斯分布是最大熵分布,所以这个值肯定是正的,而且z离高斯分布越远,那么这个值就越大。
。因为高斯分布是最大熵分布,所以这个值肯定是正的,而且z离高斯分布越远,那么这个值就越大。
我们要最大化我们的目标函数:
其中![]() 。如果我们固定
。如果我们固定![]() 是标准正交的,数据也是被白化的,那么
是标准正交的,数据也是被白化的,那么![]() 的协方差矩阵就会是
的协方差矩阵就会是![]() ,所以左边那一项就会是常数,所以
,所以左边那一项就会是常数,所以
我们可以看到,这和最大似然估计的结果其实是一样的。
12.6.4.2 最小化互信息
测量随机变量的依赖性的一个量就是多元信息: ,我们希望它们是独立的,所以我们就要最小化
,我们希望它们是独立的,所以我们就要最小化![]() ,由于
,由于![]() ,我们有
,我们有 ,假设
,假设![]() 标准正交的,那么最后一项又可以被扔掉,因为旋转变换并不会改变分布的形状。那么我们看到剩下的形式又是和最大似然估计是一样的。
标准正交的,那么最后一项又可以被扔掉,因为旋转变换并不会改变分布的形状。那么我们看到剩下的形式又是和最大似然估计是一样的。
12.6.4.3 最大化互信息
我们定义一个network,其中![]() 是输入,
是输入,![]() 是有噪的输出,
是有噪的输出,![]() 是一个非线性的函数以及
是一个非线性的函数以及![]() ,试图通过这个系统最大化信息流似乎是合理的,这一原则被称为infomax(这里我并不懂,只是有人说明了这么做是合理的)。因此我们就是最大化
,试图通过这个系统最大化信息流似乎是合理的,这一原则被称为infomax(这里我并不懂,只是有人说明了这么做是合理的)。因此我们就是最大化![]() 和
和![]() 的互信息。我们有
的互信息。我们有![]() ,根据4.1.4章中,我们有,高斯分布的熵只与方差有关,所以第二项是一个常数。并且有人计算出:
,根据4.1.4章中,我们有,高斯分布的熵只与方差有关,所以第二项是一个常数。并且有人计算出:
由于![]() 是标准正交的,所以最后一项可以扔掉。如果我们定义
是标准正交的,所以最后一项可以扔掉。如果我们定义![]() 是cdf,那么
是cdf,那么![]() 就是pdf,上面的式子跟最大似然是一样的。如果我们使用logistic非线性,
就是pdf,上面的式子跟最大似然是一样的。如果我们使用logistic非线性,![]() ,那么其实
,那么其实![]() 。
。