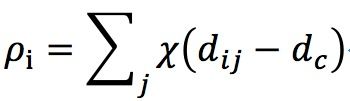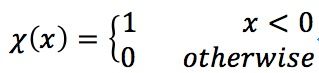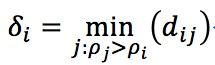Clustering By Fast Search And Find Of Density Peaks -- Sci14发表的聚类算法

This post is about a new cluster algorithm published by Alex Rodriguez and Alessandro Laio in the latest Science magazine. The method is short and efficient, I implemented it using about only 100 lines of cpp code.

BASIC METHOD

There are two leading criteria in this method: Local Density and Minimum Distance with higher density.

Rho above is the local density, in which,

and dc is a cutoff distance. Rho is basically equal to the number of points that are closer than dc to point i. The algorithm is sensitive only to the relative magnitude of rho in different points, implying that, for large data sets, the results of the analysis are robust with respect to the choice of dc.

The authors say that we can choose dc so that the average number of neighbors is around1 to 2% of the total number of points in the data set (I used 1.6% in my code).

Delta is measured by computing the minimum distance between the point i and any other point with higher density:

and for the point with highest density, we simply let:

The following figure illustrates the basic algorithm:

The left hand figure shows the dataset we use (28 points in a 2d space), most of the points belong to 2 clusters: blue and red, and there are 3 outliers with black circles. By calculating the rho and delta of each point in the dataset, we show the result by the right hand figure (decision graph), x-axis is local density, y-axis is the minimum distance between one point and any other point with higher density.

Our target is to find points that have both high rho and high delta (in this example point number 1 and 10), they’re cluster centers. We can see the three outliers (26, 27, 28) have high delta but very low rho.

CODE

// Clustering by fast search and find of density peaks

1. // Science 27 June 2014:
2. // Vol. 344 no. 6191 pp. 1492-1496
3. // DOI: 10.1126/science.1242072
4. // http://www.sciencemag.org/content/344/6191/1492.full//
5. //
6. // Code Author: Eric Yuan
7. // Blog: http://eric-yuan.me
8. // You are FREE to use the following code for ANY purpose.
9. //
10. // Have fun with it
11.  
12. #include "iostream"
13. #include "vector"
14. #include "math.h"
15. using namespace std;
16.  
17. #define DIM 3
18. #define elif else if
19.  
20. #ifndef bool
21.      #define bool int
22.      #define false ((bool)0)
23.      #define true  ((bool)1)
24. #endif
25.  
26. struct Point3d  {
27.      double x;
28.      double y;
29.      double z;
30.     Point3d ( double xin,  double yin,  double zin )  : x (xin ), y (yin ), z (zin )  { }
31. };
32.  
33. void dataPro (vector <vector  >  &src, vector  &dst ) {
34.      for ( int i  =  0; i  < src. size ( ); i ++ ) {
35.         Point3d pt (src [i ] [ 0 ], src [i ] [ 1 ], src [i ] [ 2 ] );
36.         dst. push_back (pt );
37.      }
38. }
39.  
40. double getDistance (Point3d  &pt1, Point3d  &pt2 ) {
41.      double tmp  = pow (pt1. x  - pt2. x,  2 )  + pow (pt1. y  - pt2. y,  2 )  + pow (pt1. z  - pt2. z,  2 );
42.      return pow (tmp,  0.5 );
43. }
44.  
45. double getdc (vector  &data,  double neighborRateLow,  double neighborRateHigh ) {
46.      int nSamples  = data. size ( );
47.      int nLow  = neighborRateLow  * nSamples  * nSamples;
48.      int nHigh  = neighborRateHigh  * nSamples  * nSamples;
49.      double dc  =  0.0;
50.      int neighbors  =  0;
51.     cout < < "nLow = " < <nLow < < ", nHigh = " < <nHigh < <endl;
52.      while (neighbors  < nLow || neighbors  > nHigh ) {
53.      //while(dc <= 1.0){
54.         neighbors  =  0;
55.          for ( int i  =  0; i  &lt; nSamples  -  1; i ++ ) {
56.              for ( int j  = i  +  1; j  &lt; nSamples; j ++ ) {
57.                  if (getDistance (data [i ], data [j ] )  &lt; = dc )  ++neighbors;                  if (neighbors  &gt; nHigh )  goto DCPLUS;
58.              }
59.          }
60. DCPLUS : dc  +=  0.03;
61.         cout &lt; &lt; "dc = " &lt; &lt;dc &lt; &lt; ", neighbors = " &lt; &lt;neighbors &lt; &lt;endl;
62.      }
63.      return dc;
64. }
65.  
66. vector getLocalDensity (vector  &amp;points,  double dc ) {
67.      int nSamples  = points. size ( );
68.     vector rho (nSamples,  0 );
69.      for ( int i  =  0; i  &lt; nSamples  -  1; i ++ ) {
70.          for ( int j  = i  +  1; j  &lt; nSamples; j ++ ) {
71.              if (getDistance (points [i ], points [j ] )  &lt; dc ) {
72.                  ++rho [i ];
73.                  ++rho [j ];
74.              }
75.          }
76.          //cout<<"getting rho. Processing point No."<<i<<endl;
77.      }
78.      return rho;
79. }
80.  
81. vector getDistanceToHigherDensity (vector  &amp;points, vector  &amp;rho ) {
82.      int nSamples  = points. size ( );
83.     vector delta (nSamples,  0.0 );
84.  
85.      for ( int i  =  0; i  &lt; nSamples; i ++ ) {
86.          double dist  =  0.0;
87.         bool flag  =  false;
88.          for ( int j  =  0; j  &lt; nSamples; j ++ ) {              if (i  == j )  continue;              if (rho [j ]  &gt; rho [i ] ) {
89.                  double tmp  = getDistance (points [i ], points [j ] );
90.                  if ( !flag ) {
91.                     dist  = tmp;
92.                     flag  =  true;
93.                  } else dist  = tmp  &lt; dist ? tmp  : dist;
94.              }
95.          }
96.          if ( !flag ) {
97.              for ( int j  =  0; j  &lt; nSamples; j ++ ) {                  double tmp  = getDistance (points [i ], points [j ] );                 dist  = tmp  &gt; dist ? tmp  : dist;
98.              }
99.          }
100.         delta [i ]  = dist;
101.          //cout<<"getting delta. Processing point No."<<i<<endl;
102.      }
103.      return delta;
104. }
105.  
106. int main ( int argc,  char ** argv )
107. {
108.      long start, end;
109.     FILE  *input;
110.     input  = fopen ( "dataset.txt",  "r" );
111.     vector &lt;vector  &gt; data;
112.      double tpdouble;
113.      int counter  =  0;
114.      while ( 1 ) {
115.          if (fscanf (input,  "%lf",  &amp;tpdouble ) ==EOF )  break;
116.          if (counter  /  3  &gt; = data. size ( ) ) {
117.             vector tpvec;
118.             data. push_back (tpvec );
119.          }
120.         data [counter  /  3 ]. push_back (tpdouble );
121.          ++ counter;
122.      }
123.     fclose (input );
124.      //random_shuffle(data.begin(), data.end());
125.  
126.     start  = clock ( );
127.     cout &lt; &lt; "********" &lt; &lt;endl;
128.     vector points;
129.     dataPro (data, points );
130.      double dc  = getdc (points,  0.016,  0.020 );
131.     vector rho  = getLocalDensity (points, dc );
132.     vector delta  = getDistanceToHigherDensity (points, rho );
133. //    saveToTxt(rho, delta);
134.      // now u get the cluster centers
135.     end  = clock ( );
136.     cout &lt; &lt; "used time: " &lt; &lt; ( ( double ) (end  - start ) )  / CLOCKS_PER_SEC &lt; &lt;endl;
137.      return  0;
138. }

PostScript: I found that the result differs a lot when using different value of dc, If you have any idea of how to calculate dc precisely, please let me know.

Newly Updated: Jul. 1 9:14 Pm

Ryan raised an interesting idea yesterday and I tried it.

ryan

Here’s the new function to calculate “Local Density”:

vector getAverageKnnDistance(vector &points){

1.      double ratio  =  0.015;
2.      int nSamples  = points. size ( );
3.      int M  = nSamples  * ratio;
4.     vector rho (nSamples,  0.0 );
5.      for ( int i  =  0; i  &lt; nSamples; i ++ ) {
6.         vector tmp;
7.          for ( int j  =  0; j  &lt; nSamples; j ++ ) {
8.              if (i  == j )  continue;
9.              double dis  = getDistance (points [i ], points [j ] );
10.              if (tmp. empty ( ) ) {
11.                 tmp. push_back (dis );
12.              }elif (tmp. size ( )  &lt; M ) {
13.                  if (dis  &lt; = tmp [tmp. size ( )  -  1 ] ) tmp. push_back (dis );
14.                  else {
15.                      for ( int k  =  0; k  &lt; tmp. size ( ); k ++ ) {
16.                          if (tmp [k ]  &lt; = dis ) {                             tmp. insert (tmp. begin ( )  + k, dis );                              break;                          }                      }                  }              } else {                  if (dis  &gt; = tmp [ 0 ] ) {
17.                     ;  // do nothing
18.                  }elif (dis  &lt; = tmp [tmp. size ( )  -  1 ] ) {
19.                     tmp. erase (tmp. begin ( ) );
20.                     tmp. push_back (dis );
21.                  } else {
22.                      for ( int k  =  0; k  &lt; tmp. size ( ); k ++ ) {
23.                          if (tmp [k ]  &lt; = dis ) {
24.                             tmp. insert (tmp. begin ( )  + k, dis );
25.                             tmp. erase (tmp. begin ( ) );
26.                              break;
27.                          }
28.                      }
29.                  }
30.              }
31.          }
32.          double res  =  0.0;
33.          for ( int j  =  0; j  &lt; tmp. size ( ); j ++ ) {
34.             res  += tmp [j ];
35.          }
36.         rho [i ]  =  0  - res  / tmp. size ( );
37.      }
38.      return rho;
39. }

Because the mean distance to nearest M neighbors is inversely proportional to density, so I add a “y = -x” in the end.

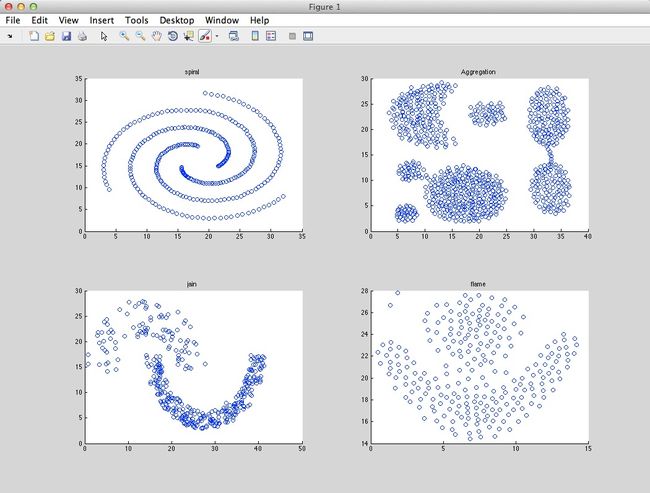
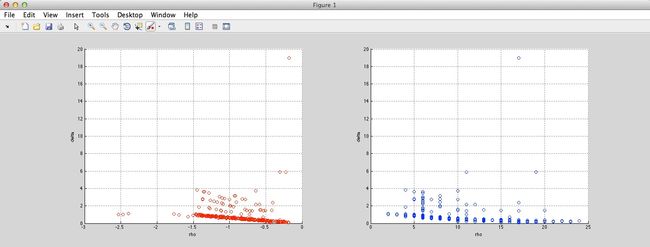
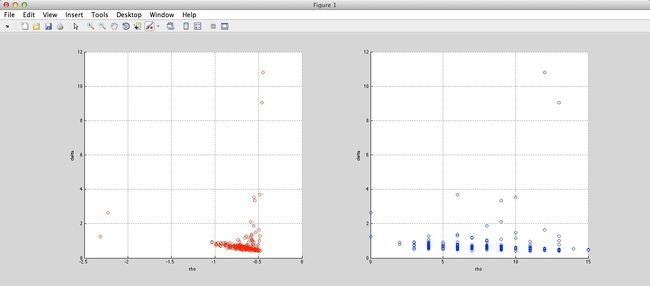
I tested this idea using four dataset:

• Aggregation: 788 vectors, 2 dimensions, 7 clusters.
• Spiral: 312 vectors, 2 dimensions, 3 clusters
• Jain: 373 vectors, 2 dimensions, 2 clusters
• Flame: 240 vectors, 2 dimensions, 2 clusters

And the result is as follow (Ryan’s idea in red circles, method in paper in blue circles):

Jain:

Spiral:

Flame:

Aggregation:

Actually Ryan’s method works well, but just like I replied him, how to get a proper “M” is still like black magic.

If anyone has any idea, please let me know.

Thanks Ryan.

 

原文：http://eric-yuan.me/clustering-fast-search-find-density-peaks/

备注：

对于作者原来的论文里面有一个超参 (d_c) 设置会影响效果；但该算法能处理不同密度的簇。

对于Ryan's 的方法，同样的M=#sample * 0.015 也是一个经验值，需要设定或调节。但这个方法貌似比较好。

文献出处：

http://www.52ml.net/16351.html

http://www.52ml.net/16296.html （中文）