线性规划与非线性规划的求解

一、单纯法求解线性规划的原理

一般线性规划问题中当线性方程组的变量数大于方程个数，这时会有不定数量的解，而单纯形法是求解线性规划问题的通用方法。
具体步骤是，从线性方程组找出一个个的单纯形，每一个单纯形可以求得一组解，然后再判断该解使目标函数值是增大还是变小了，决定下一步选择的单纯形。通过优化迭代，直到目标函数实现最大或最小值。
换而言之，单纯形法就是秉承“保证每一次迭代比前一次更优”的基本思想：先找出一个基本可行解，对它进行鉴别，看是否是最优解；若不是，则按照一定法则转换到另一改进后更优的基本可行解，再鉴别；若仍不是，则再转换，按此重复进行。因基本可行解的个数有限，故经有限次转换必能得出问题的最优解。如果问题无最优解，也可用此法判别。

二 、Excel求解线性规划

1、Excel使用大M法求解线性规划

2、Excel使用规划求解包进行求解线性规划

可以得出x1，x2，x3的值

通过上述结果可以看出求解出来的值与大M法求解的值相同

三、线性规划

1、Python调用optimize包和scipy求解线性规划

也用Excel中的约束条件
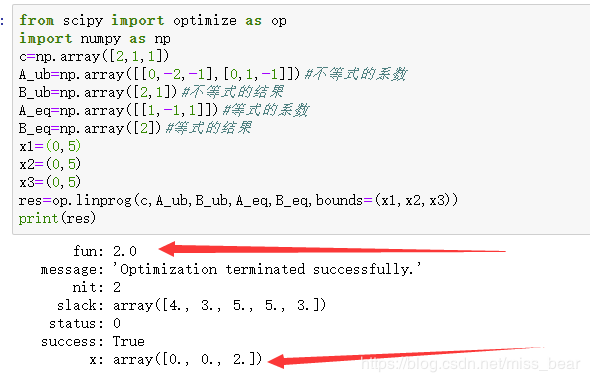
代码如下图所示

from scipy import optimize as op
import numpy as np
c=np.array([2,1,1])
A_ub=np.array([[0,-2,-1],[0,1,-1]])#不等式的系数
B_ub=np.array([2,1])#不等式的结果
A_eq=np.array([[1,-1,1]])#等式的系数
B_eq=np.array([2])#等式的结果
x1=(0,5)
x2=(0,5)
x3=(0,5)
res=op.linprog(c,A_ub,B_ub,A_eq,B_eq,bounds=(x1,x2,x3))
print(res)

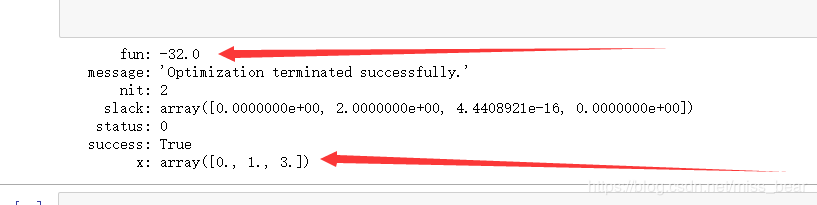
运算出来的结果（我们主要关注第一行与最后一行，第一行就是就是出来的值，最后一行就是x的值）

2、Python编程实现单纯法

（此处我换了一个约束条件，因为用上面的约束条件一直没有输出，就换了一个约束条件）

import numpy as np

def pivot():
    l = list(d[0][:-2])
    jnum = l.index(max(l)) #转入编号
    m = []
    for i in range(bn):
        if d[i][jnum] == 0:
            m.append(0.)
        else:
            m.append(d[i][-1]/d[i][jnum])
    inum = m.index(min([x for x in m[1:] if x!=0]))  #转出下标
    s[inum-1] = jnum
    r = d[inum][jnum]
    d[inum] /= r
    for i in [x for x in range(bn) if x !=inum]:
        r = d[i][jnum]
        d[i] -= r * d[inum]
        
def solve():
    flag = True
    while flag:
        if max(list(d[0][:-1])) <= 0: #直至所有系数小于等于0
            flag = False
        else:
            pivot()
            
def printSol():
    for i in range(cn - 1):
        if i in s:
            print("x"+str(i)+"=%.2f" % d[s.index(i)+1][-1])
        else:
            print("x"+str(i)+"=0.00")
    print("objective is %.2f"%(-d[0][-1]))

d = np.loadtxt("data1.txt", dtype=np.float)
(bn,cn) = d.shape
s = list(range(cn-bn,cn-1)) #基变量列表
solve()
printSol()

运算出来的结果

注意，需要加载本地的txt文件

3、采用上面的这个约束条件，使用调用python库的方式计算结果对比

代码如下

from scipy import optimize
import numpy as np
#确定c,A_ub,B_ub
c = np.array([1,14,6])
A_ub = np.array([[1,1,1],[1,0,0],[0,0,1],[0,3,1]])
B_ub = np.array([4,2,3,6])
res =optimize.linprog(-c,A_ub,B_ub)
print(res)

运行结果

四、非线性规划

1、直接调用python中的库

代码如下所示

# coding=utf-8
from scipy.optimize import minimize
import numpy as np
 
# demo 2
#计算  (2+x1)/(1+x2) - 3*x1+4*x3 的最小值  x1,x2,x3的范围都在0.1到0.9 之间
def fun(args):
    a,b,c,d=args
    v=lambda x: (a+x[0])/(b+x[1]) -c*x[0]+d*x[2]
    return v
def con(args):
    # 约束条件 分为eq 和ineq
    #eq表示 函数结果等于0 ； ineq 表示 表达式大于等于0  
    x1min, x1max, x2min, x2max,x3min,x3max = args
    cons = ({'type': 'ineq', 'fun': lambda x: x[0] - x1min},\
              {'type': 'ineq', 'fun': lambda x: -x[0] + x1max},\
             {'type': 'ineq', 'fun': lambda x: x[1] - x2min},\
                {'type': 'ineq', 'fun': lambda x: -x[1] + x2max},\
            {'type': 'ineq', 'fun': lambda x: x[2] - x3min},\
             {'type': 'ineq', 'fun': lambda x: -x[2] + x3max})
    return cons
 
if __name__ == "__main__":
    #定义常量值
    args = (2,1,3,4)  #a,b,c,d
    #设置参数范围/约束条件
    args1 = (0.1,0.9,0.1, 0.9,0.1,0.9)  #x1min, x1max, x2min, x2max
    cons = con(args1)
    #设置初始猜测值  
    x0 = np.asarray((0.5,0.5,0.5))
    
    res = minimize(fun(args), x0, method='SLSQP',constraints=cons)
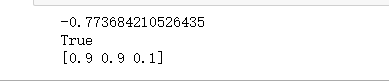
    print(res.fun)
    print(res.success)
    print(res.x)

五、对比单纯法与直接调用库

因为直接调用库的约束条件与Excel是相同的，因此可以对比出结果是相同的，但是单纯法采用的约束条件不同，所以单纯法结果就不与Excel结果比较。后面直接直接调用python库采用了与单纯法相同的约束条件，可以对比出来结果是相同的，基本没有误差！