iGraph库中Community Detection方法比较



    复杂网络的使用中，有这么几个库：

表格来自：http://bbs.sciencenet.cn/blog-404069-297233.html

库名称	原始开发语言	可用某语言调用
BGL	C++	C++/ Python（通过boost-python）
QuickGraph	C#	支持.NET平台的任何语言(Python程序员可用IronPython)
igraph	C	C/C++/R/Python（理论上至少有50种语言可直接或间接调用C程序）
NetworkX	Python	Python

=========
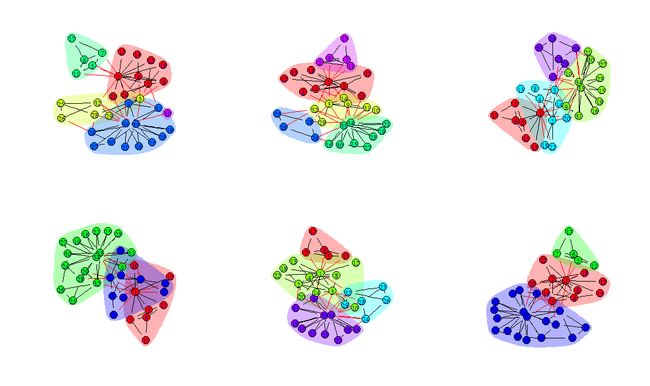
别的没有尝试过，igraph还是比较好用的，里面的社区发现经典算法很全面。直接贴对比几种方法的R代码吧，相关论文以及算法的复杂度都在代码中，自己体验体验吧，multilevel.community（算法可以称作：Louvain或者BGLL）算法感觉是稳定、准确而且快速的，特别是稀疏图的时候：没时间细说原理了，其实原理都很简单。

library(igraph)
layout(matrix(c(1,2,3,
 4,5,6),nr = 2, byrow = T))

##########################################################
#经典的“Zachary 空手道俱乐部”（Zachary‟s Karate Club）社
#会网络[26]。20 世纪70 年代，Zachary 用了两年的时间观察美国一所大学的空手道
#俱乐部内部成员间关系网络。在Zachary 调查的过程中，该俱乐部的主管与校长因
#为是否提高俱乐部收费的问题产生了争执，导致该俱乐部最终分裂成了两个分别
#以主管与校长为核心的小俱乐部。就模块度优化而言，当前学者们已经广泛认为，
#该网络的最优划分是模块度Q=0.419 的4 个社团划分。
##########################################################
g <- graph.famous( "Zachary" )

##
#• Community structure in social and biological networks
# M. Girvan and M. E. J. Newman
#• New to version 0.6: FALSE
#• Directed edges: TRUE
#• Weighted edges: TRUE
#• Handles multiple components: TRUE
#• Runtime: |V||E|^2 ~稀疏:O(N^3)
##
system . time (ec <- edge.betweenness.community(g))
print(modularity(ec))
plot(ec, g)

#• Computing communities in large networks using random walks
# Pascal Pons, Matthieu Latapy
#• New to version 0.6: FALSE
#• Directed edges: FALSE
#• Weighted edges: TRUE
#• Handles multiple components: FALSE
#• Runtime: |E||V|^2
system . time (wc <- walktrap.community(g))
print(modularity(wc))
#membership(wc)
plot(wc , g)
#• Finding community structure in networks using the eigenvectors of matrices
# MEJ Newman
# Phys Rev E 74:036104 (2006)
#• New to version 0.6: FALSE
#• Directed edges: FALSE
#• Weighted edges: FALSE
#• Handles multiple components: TRUE
#• Runtime: c|V|^2 + |E| ~N(N^2)
system . time (lec <-leading.eigenvector.community(g))
print(modularity(lec))
plot(lec,g)

#• Finding community structure in very large networks
# Aaron Clauset, M. E. J. Newman, Cristopher Moore
#• Finding Community Structure in Mega-scale Social Networks
# Ken Wakita, Toshiyuki Tsurumi
#• New to version 0.6: FALSE
#• Directed edges: FALSE
#• Weighted edges: TRUE
#• Handles multiple components: TRUE
#• Runtime: |V||E| log |V|
system . time (fc <- fastgreedy.community(g))
print(modularity(fc))
plot(fc, g)

#• Fast unfolding of communities in large networks
# Vincent D. Blondel, Jean-Loup Guillaume, Renaud Lambiotte, Etienne Lefebvre
#• New to version 0.6: TRUE
#• Directed edges: FALSE
#• Weighted edges: TRUE
#• Handles multiple components: TRUE
# Runtime: “linear” when |V| \approx |E| ~ sparse; (a quick glance at the algorithm \
# suggests this would be quadratic for fully-connected graphs)
system . time (mc <- multilevel.community(g, weights=NA))
print(modularity(mc))
plot(mc, g)

#• Near linear time algorithm to detect community structures in large-scale networks.
# Raghavan, U.N. and Albert, R. and Kumara, S.
# Phys Rev E 76, 036106. (2007)
#• New to version 0.6: TRUE
#• Directed edges: FALSE
#• Weighted edges: TRUE
#• Handles multiple components: FALSE
# Runtime: |V| + |E|
system . time (lc <- label.propagation.community(g))
print(modularity(lc))
plot(lc , g)

其中BGLL算法还是既稳定又快速的方法，LPA方法也太不稳定了吧。