Slam 14讲学习笔记 —— 第五讲 —— 相机与图像
本讲主要搞清楚相机的针孔模型、透镜的畸变模型。从而弄清成像(外部的三维点投影到相机内部成像平面)及相机的内外参。
一. 相机模型:针孔(小孔)成像模型:
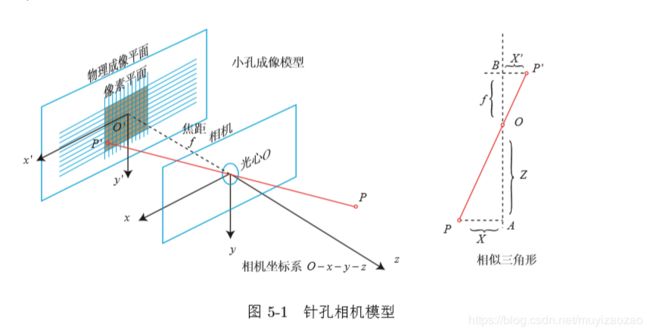
上图的几何模型如下:
O—x—y—z为相机坐标系(z指向相机的前方,x指向相机的右方,y指向下,O为相机的光心)。成像平面O’—x’—y’,现实世界的P点经过相机光心(小孔)投影后在成像平面上为像点P’。
设P点坐标为[X,Y,Z],P’坐标为[X’,Y’,Z’],并设焦距(光心到成像平面的距离)为f,则有:
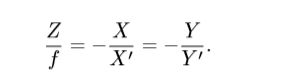 负号表示成像为倒的,为了简化模型,可以把成像平面对称到相机前方:
负号表示成像为倒的,为了简化模型,可以把成像平面对称到相机前方:
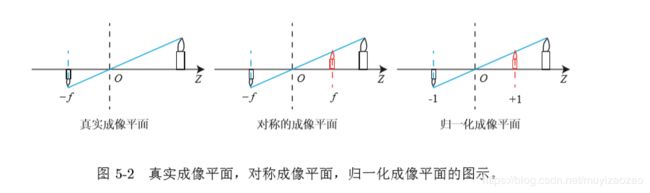
所以上式变为:
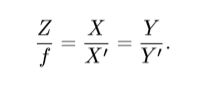
整理后:

上式描述了物理空间点P和它的像点P’的空间关系。
但是我们在相机中获得的是一个个的像素,需要在成像平面对像进行采样和量化。为了将相机上感受的光线转化为图像像素,设在成像平面(原点对称到相机前方)上有一像素平面o-u-v。在像素平面得到P’的坐标为(u,v)。
直接得出“P点的像”在像素平面的像素坐标(u,v)和空间点P在相机坐标下的坐标(X,Y,Z)的关系:
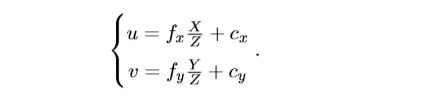
注:fx = af;fy=bf;f为焦距
a:像素坐标在u轴上缩放了a倍
b:像素坐标在v轴上缩放了b倍
原点平移了[cx,cy]
这里的缩放和平移我也不明白,只能按照书中这样写。
将上式写成矩阵形式:
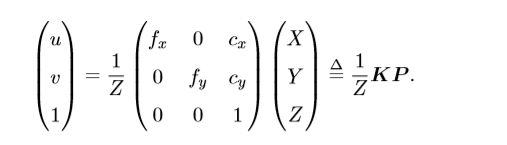
按照传统的习惯,将Z移到左侧:
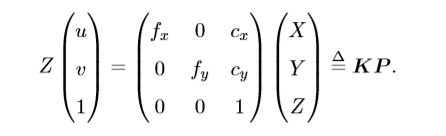
所以相机的内参数矩阵K就是上式的中间的矩阵。
相机的内参K:
1)相机的厂商告诉内参。使用过程中不会变化。
2)自己标定。(标定算法 )
相机的外参:
因为P点坐标[X,Y,Z]是在相机的坐标系下的,设P点的世界坐标为Pw,而P[X,Y,Z]应是世界坐标系下的坐标Pw加上旋转平移后而来的,所以用世界坐标系改写为:

注:
- 上式的R(旋转矩阵)和t就是相机的外参。
- Puv即[u,v,1]T,后面的就是带入了P=RPw+t(旋转矩阵),再用T变换矩阵改写。
- R为3乘3矩阵,而T为4乘4矩阵,Pw是三维空间坐标的转置为3*1,所以,要给Pw添加一维[Pw,1]T,仍记为Pw。TPw为4乘1向量,而K是3乘3矩阵,所以取TPw的前三维(第四维为1)与K做乘法。
又因为Z是P点在相机坐标系下的坐标值,当把其化为 1时,P即成为了归一化平面上的一点,将P点投影到Z=1的平面上,该点的投影坐标为:P投影=[X/Z,Y/Z,1],这个形式与Puv=[u,v,1]一致。所以我们可以把像素坐标看成对归一化平面的点进行量化测量的结果。
二. 畸变
- 产生畸变的原因:
1)相机的透镜的加入,光线的传播不再是直线。——径向畸变。
2)相机内,成像平面和透镜不一定是完全平行的。 ——切向畸变。
其中,径向畸变可分为:桶形畸变、枕形畸变。
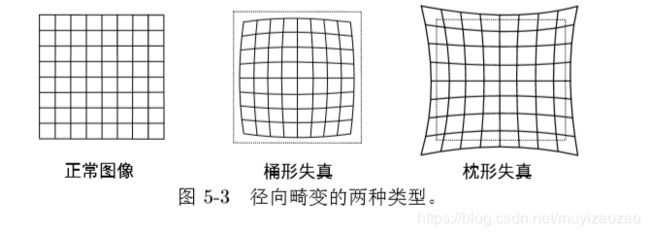
注:
1)桶形畸变是由于图像放大率随着离光轴的距离增加而减小,而枕形畸变却恰好相反。 在这两种畸变中,穿过图像中心和光轴有交点的直线还能保持形状不变。
2)径向畸变可看成 坐标点沿着长度方向发生了变化 δr, 也就是其距离原点的长度发生了变化。切向畸变可以 看成坐标点沿着切线方向发生了变化,也就是水平夹角发生了变化 δθ。
- 畸变的矫正:
1)对于径向畸变,用和距中心距离有关的二次及高次多项式进行矫正:

注:
1)其中 [x,y]T 是未纠正的点的坐标,[xcorrected,ycorrected]T是纠正后的点的坐标,注意它们 都是归一化平面上的点,而不是像素平面上的点。
2)对于畸变较小的图像中心区域,畸变纠正主要是 k1 起作用。而对于畸变较大的边缘区域主要是 k2 起作用。普通摄像头用这两个系数就能很 好的纠正径向畸变。对畸变很大的摄像头,比如鱼眼镜头,可以加入 k3 畸变项对畸变进行 纠正。
对于一个空间点,它的畸变校正过程如下:
- 将三维空间点投影到归一化图像平面。设它的归一化坐标为 [x,y]T。
- 对归一化平面上的点进行径向畸变和切向畸变纠正。

- 将纠正后的点通过内参数矩阵投影到像素平面,得到该点在图像上的正确位置。

注:在上面的纠正畸变的过程中,我们使用了五个畸变项。实际应用中,可以灵活选择校正模型,比如只选择 k1,p1,p2 这三项等。
最后,我们小结一下单目相机的成像过程:
- 首先,世界坐标系下有一个固定的点 P,世界坐标为 Pw;
- 由于相机在运动,它的运动由 R,t 或变换矩阵 T ∈ SE(3) 描述。P 的相机坐标为: ˜ Pc = RPw + t。
- 这时的 ˜ Pc 仍有 X,Y,Z 三个量,把它们投影到归一化平面 Z = 1 上,得到 P 的归 一化相机坐标:Pc = [X/Z,Y /Z,1]T 。
- 最后,P 的归一化坐标经过内参后,对应到它的像素坐标:Puv = KPc。
综上所述,我们一共谈到了四种坐标:世界、相机、归一化相机和像素坐标。请读者 理清它们的关系,它反映了整个成像的过程。
双目相机的模型:
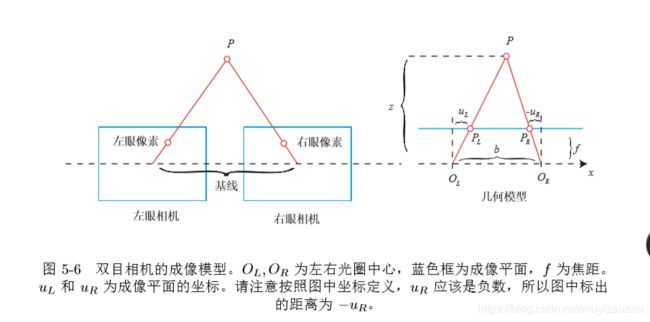
注:
1)左右两个相机都可以看成单目的相机。
2)两个相机的光圈中心都在x轴上,他们的距离称为双目相机的基线(b)。
3)考虑一个空间点 P,它在左眼和右眼各成一像,记作 PL,PR。由于相机基线的存在,这两个成像位置是不同的。理想情况下,由于左右相机只有在 x 轴上有位移,因此 P 的像也只在 x 轴(对应图像的 u 轴)上有差异。我们记它在左侧的坐标为 uL,右侧坐标 为 uR。那么,它们的几何关系如图5-6右侧所示。根据三角形 P−PL−PR 和 P−OL−OR 的相似关系,有:
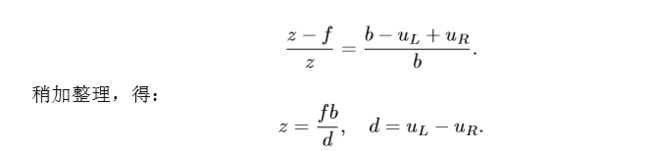
这里的d即为视差
4)基线越大,能测的距离越远;视差越大,该像素距离越近。
5)优缺点:能得到深度信息;d的确定(图像纹理丰富的地方才能确定),d的计算复杂。
RGB相机模型:
- RGB-D相机可按原理分为两类:1)红外结构光;2)脉冲光(TOF,飞行时间法)
- 在测量深度之后,相机自己完成深度与彩色图像素的配对,输出一一对应的彩色图和深度图。对RGB-D数据,既可以在图像层面处理,也可以生成点云处理。
- 缺点:成本高;功耗大。容易受日光或其他传感器发射的红外光干扰,不能再室外使用;同时使用多个也会相互干扰;对于投射材质的物体,无法使用。
