2018 UESTC ACM Summer Training Team Selection (3) (赛后补题)
2018 UESTC ACM Summer Training Team Selection (3)
由于自己水平有限,补题补的都是感觉应该能做出来的题目。(包括水过去的和没做出来的)
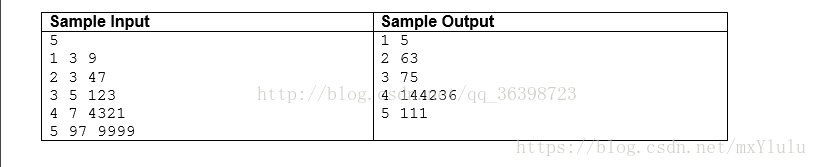
由样例我们可以发现,9可以以为基础被拆分成3^2、3^1、3^0,这三种情况综合起来的总次数就是答案。
动规方程为dp[n][k](k表示最大的数不超过m^k),dp[n][k]=dp[n][k-1]+dp[n-m^k][k];
意思为数字为n且分离出的数字最大不超过m^k的种类等于:
1、完全没有m^k的n分出的种类(最大数不超过m^(k-1))
2、已经放了一个 m^k(有可能还能放一个所以数字为n-m^k,但最大数仍然不超过m^k,也许还能再放一个:比如9^3-1放了一个9^2是不是还能放一个9^2?当然9^3不可能放进去)
接下来是代码:
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
然后引用一下这位大牛得优化代码:滚动数组真的强。/我这份代码有可能TLE(比赛过后交不了题了QAQ不能确定)/
https://blog.csdn.net/qq_36398723/article/details/77304611
采取这样得方式就不需要考虑i没有刚好满足j需求得情况(见前面注释为什么少了一些次数)
#include
#include
#include
#include
using namespace std;
typedef long long llt;
llt dp[10010];
int quick_pow(int n,int k)
{
int ans=1;
while(k)
{
if(k&1) ans*=n;
n*=n;
k>>=1;
}
return ans;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
memset(dp,0,sizeof(dp));
int a,b,n;
scanf("%d%d%d",&a,&b,&n);
int max_pack=0;
//quick_pow(b,max_pack)表示能从n中划分出最大的数
while(quick_pow(b,max_pack+1)<=n) max_pack++;
for(int i=0;i<=n;i++) dp[i]=1;
//滚动数组优化
for(int i=1;i<=max_pack;i++)
{
int p=quick_pow(b,i);
for(int j=p;j<=n;j++)
{
dp[j]=dp[j]+dp[j-p];
}
}
printf("%d %lld\n",a,dp[n]);
}
return 0;
}
这道题。
因为自己独立思考得能力还是太差得缘故。想到了正向往下推log n得复杂度可以接受,但是没想到反向推回来.....
正向往下推是越推越多,写了一份代码就不写出来了,到后面程序都算不出来了(也有可能数组装不下来反正程序不得过)
但是回推就能保证走最少的步数。QAQ很好想但是比赛花了快两个小时一直写不出来。叹气。应该蛮简单得一道题。
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
值得注意的是刚刚手写了一下代码,fun函数中我定义Node T,一开始没有这一步,所有的T都是fun(n/2),对于每一个这个全都进行一次回退(其实用T回退一次就够了)然后因为这个小失误倒置最后一个数据
1431655765算了好几分钟都没算出来。
这道题我想到的思路是首先枚举出第一个下降序列,再枚举出第二个,再枚举第三个,接着对于每个枚举出来的情况,把剩下的上升序列插入进去(注意保证插入过后不会产生新的下降序列)例如12345,k=2,枚举21、31、41、51、32....出来之后选第一个,再选第二个(数字不能重复),比如选了21、43接下来就是把5插入到*21*43*中,保证合法性的情况只有最右边能插入。
这样的思路算出结果应该是没问题...但是一直想不出来怎么实现。
然后上网查了一下...结果是动态规划,果然自己DP学的还是太差了...
参考了一下:https://blog.csdn.net/lwgkzl/article/details/76033662
dp方程中dp[i][j]表示数字为1~i时有j个下降序列的排列种数。然后就是写的超级棒的dp方程(也可能我太菜了。)
对于dp[i][j],从上一步的状态1:dp[i-1][j]意味着下降序列已经定好,这个时候由于i对于之前的1~i-1必然是大于的,所以放在出最后一位之外的位置(放在最后一位就是一种情况啦)一般是会使下降序列增加的,除非放在下降序列中,比如1 3 2 7 4 5 6这个序列,放8的时候如果放在3、2或者7、4中会变成3、8、2和7、8、4。稍微证明一下对于下降序列m+k,m,(m+k<=i-1),i插入到中间之后m+k,i必然升序,i,m必然降序,如果放在其他位置(最后一个除外)i,m必然形成新的下降序列。
dp[i][j]=状态1(dp[i-1][j]*(j+1))+状态2
从上一步的状态2:dp[i-1][j-1]从上面的分析中我们可以看出j+1的位置不会改变下降序列,而事实上一旦改变必然增加一个,那么总共i+1的位置,一共有i+1-(j+1)的位置会增加一个。
所以dp方程为:dp[i][j]=dp[i-1][j-1]*(j+1)+dp[i-1][j]*(i-j);
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include