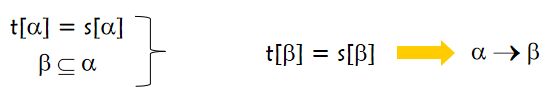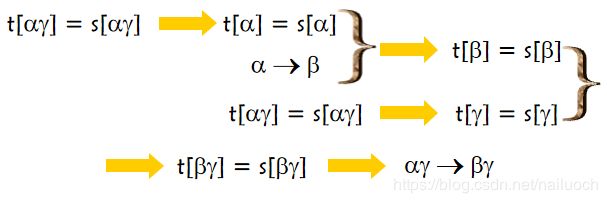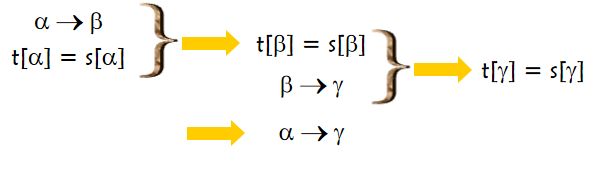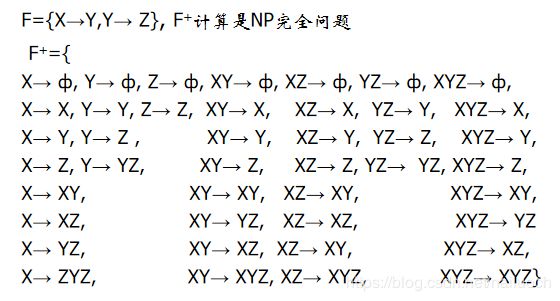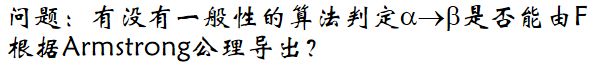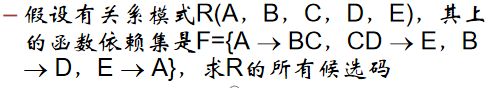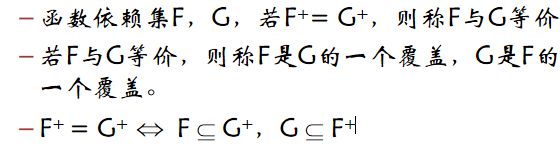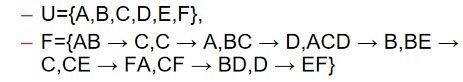(13)函数依赖的推理规则(armstrong公理)
目录
问题引入:
1.逻辑蕴涵
2.Armstrong公理系统
3.函数依赖的闭包
4.属性集闭包
5.候选码的求解理论和算法
6.函数依赖集的规范覆盖
问题引入:
①除了给定的函数依赖,我们需要考虑模式上成立的所有函数依赖?
② 给定一组函数依赖,是否能导出另外一些函数依赖,或另外的函数依赖是否成立。 如FD={A ->B,B -> C},A ->C是否成立?
1.逻辑蕴涵
这个概念是针对第二个问题提出的,即给定一组函数依赖能否导出另一些函数依赖。
定义:设有关系模式R(U)及其函数依赖集F,如果对于R的任一个满足F的关系r函数依赖X→Y都成立,则称F逻辑蕴涵X→Y,或称X→Y可以由F推出。记作F |= X→Y。例:关系模式 R=(A,B,C),函数依赖集F={A→B,B→C}, F逻辑蕴涵A→C。
证:设u,v为r中任意两个元组:
若A→C不成立,则有u[A]=v[A],而u[C]≠v[C]
而且A→B, B→C,知
u[A]=v[A], u[B]=v[B], u[C]=v[C],
即若u[A]=v[A]则u[C]=v[C],和假设矛盾。
故F逻辑蕴涵A→C。满足F依赖集的所有元组都函数依赖X→Y(X→Y不属于F集),则称F逻辑蕴涵X→Y
(X→Y由F依赖集中所有依赖关系推断而出)F能推出 原不直观存在于 函数依赖集F 中的函数依赖 X→ Y,则成X→Y被函数依赖集F逻辑蕴含
2.Armstrong公理系统
Armstrong公理的正确性和完备性:
正确性是指用该公理从F中导出的函数依赖必为F所蕴含,(也就是用该公理从依赖关系集中导出的函数依赖确实是这个关系集所蕴含的)下面给出证明。
完备性是指F所蕴含的所有函数依赖都能用Armstrong公理导出。
α,β,γ,δ是属性集,按函数依赖定义r是R
①自反律
![]()
证明:
这个不解释傻瓜式证明。
②增广律
证明:
注意:t[αγ] = s[αγ]时,也就是t和s在α和γ两个属性集上取值相同,所以肯定存在t[γ] = s[γ]
③传递律
由以上公理导出以下定律:
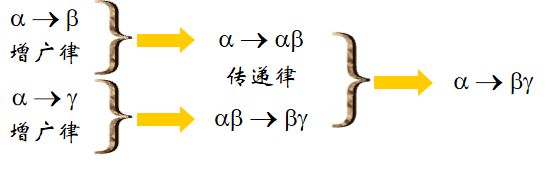
①合并率
![]()
证明过程是传递率和增广律的结合,值得一看:
②分解律
证明是自反律加传递率。
③伪传递律
证明,增广律加上传递律。
总结:
①自反(就跟废话一样,自己决定自己的子集)②增广③ 传递
④合并律 增广+传递 ⑤分解律 自反+传递 ⑥伪传递律 增广+传递
3.函数依赖的闭包
定义:若F为关系模式R(U)的函数依赖集,我们把F以及所有被F逻辑蕴涵的函数依赖的集合称为F的闭包,记为F+。
即:F+={X→Y|X→Y∈F∨“应用Armstong公理从F中导出的任何X→Y”}求函数闭包流程:
4.属性集闭包
①为什么引入属性集闭包?
②求属性集闭包的方法:
例题:
关系模式R
,其中U={A,B,C,D,E},F={AB→C,B→D,C→E,EC→B,AC→B},求(AB)+ 第一步,令X(0)=AB。
第二步,求X(1)。先列出X(0)的非空子集,即AB的非空子集为{A,B,AB}。然后扫描F集合,寻找{A,B,AB}可能存在的函数依 赖,就可以得到:AB→C,B→D。于是就可以求得X(1)=X(0)∪C∪D=ABCD。然后判断X(0)如果等于X(1)就结束,所求即为答案,如果X(0)不等于X(1)就继续计算。
第三步,求X(2)。同第二步求X(1)得非空真子集,然后在F中一次寻找函数依赖,可以得到:AB→C,B→D,C→E,AC→B。求 得X(2)=X(1)∪C∪D∪E∪B=ABCDE。这时候发现X(2)已经等于全部属性集U了,就结束计算,得出(AB)+ =ABCDE。
③属性集闭包算法的作用
说明:1.超码的属性集闭包是全部属性集。
2.避免求函数依赖闭包(复杂性高)来判断这类问题,23说的是一回事。
5.候选码的求解理论和算法
对于给定的关系R(A1,A2,…An)和函数依赖集F,可将其属性分为4类:
L类 仅出现在函数依赖左部的属性。
R 类 仅出现在函数依赖右部的属性。
N 类 在函数依赖左右两边均未出现的属性。
LR类 在函数依赖左右两边均出现的属性。
①定理:对于给定的关系模式R及其函数依赖集F,若X(X∈R)是L类属性,则X必为R的任一候选码的成员。
因为L类属性不依赖任何其他属性,所以必是候选码成员。
推论:对于给定的关系模式R及其函数依赖集F,若X(X∈R)是L类属性,且X+包含了R的全部属性;则X必为R的唯一候选码。因为L类不依赖于其他类属性,不会被其他属性推出。
例:设有关系模式R(A,B,C,D),其函数依赖集F={D→B,B →D,AD →B,AC →D},求R的所有候选码。
解:考察F发现,A,C两属性是L类属性,所以AC必是R的候选码成员,又因为(AC)+=ABCD,所以AC是R的唯一候选码。
②定理:对于给定的关系模式R及其函数依赖集F,若X(X∈R)是N类属性,则X必包含在R的任一候选码中。
推论:对于给定的关系模式R及其函数依赖集F,若X(X∈R)是L类和N类组成的属性集,且X+包含了R的全部属性;则X是R的唯一候选码。
③定理:对于给定的关系模式R及其函数依赖集F,若X(X∈R)是R类属性,则X不在任何候选码中。
总结:LN均不能由别的属性推出,所以必是候选码成员,若LN类属性闭包包含全部属性,则此属性集为唯一候选码。R类属性只能由别人推出,绝对不会出现在候选码中(候选码是最小的超码)。
重要例题:
解:ABCDE在F的各个函数依赖的右侧均出现过,因此,候选码可能包含ABCDE,我们只能试:
①先试单个的,(A)+ =ABCDE,(E)+ =ABCDE所以A,E是候选码。
②(B)+ =BD,(C)+=C,(D)+=D所以B,C,D都不是。
③两个 从BCD选,(CD)+=ABCDE,(BC)+=ABCDE所以BC,CD是
注意:如果(CD)+ = ABCDE单纯这个条件不能判断CD是否是候选码,还要判断(C)+,(D)+是不是候选码,候选码是最小的超码。
6.函数依赖集的规范覆盖
①什么是函数依赖集规范(正则)覆盖
先来说什么是覆盖:
再来引入一个概念:无关属性
如果去除一个函数依赖中的属性,不会改变该函数依赖集的闭包,则称该属性是无关的(extraneous)
重要:无关属性的核心:能够被函数依赖集F逻辑蕴涵的函数依赖,不必出现在F中
无关属性,无关FD的定义如下:
(1)如果A∈X,且F逻辑蕴含(F - {X→Y})U{(X-A)→Y},则A称为X→Y左部无关属性。
通俗一点说就是X→Y这个FD,把属性组X中的A属性去除也能得到。
(2)如果A∈X,且F逻辑蕴含(F - {X→Y})U(X→(Y-A)),则称A为X→Y的右无关属性。
(3)如果X→Y两端的属性都是无关属性,则称X→Y为无关FD。
检验无关性的方法:
总结:逐个元素看删。删左边好说,你就看看删完之后的属性集闭包能不能推出这个FD,删右边的话,假设能删除,在新的F里面计算α的闭包,看能否包括被删元素。
例题:
在①中,将AB→C的B删除,然后发现确实可以由F推出A→C,在②中删除AB→CD中的C,在新的F'中,能推出AB→C。
有了以上概念后我们就可以定义规范覆盖(Fc)
设F是属性集U上的FD集,Fc是F的一个规范覆盖,Fc应满足以下三个条件:
①(Fc)+ = F+,也就是Fc覆盖F。
②Fc中每个FD都不包含无关属性。
③Fc中每个FD左部唯一出现,即任意两个FD左部都不相等。
第三点怎么理解,A→B,A→C,可以A→BC,也就是为了简洁能合并就合并。
②规范覆盖算法(先合并,再去无关)
注:正则覆盖未必唯一。
最重要的例题,理一下流程:
求Fc:
step1:合并,发现没什么可以合并的
step2:分解左边求左边分解属性的闭包就行
AB→C,(A)+ = A,所以不成立,B→C,(B)+ = B,所以不成立
BC→D,(B)+ = B,(C)+=C,所以不成立
ACD→B,(AC)+ = AC,(AD)+=ADEF,(CD)+= ABCDEF,所以A多余
BE→C,(B)+ = B,(E)+=E
CE→FA,(C)+ = C,(E)+=E
CF→BD,(C)+ = C,(F)+=F
D→EF,左边没有可分解的
左边分解结果:F = {AB→C,C→A,BC→D,CD→B,BE→C,CE→FA,CF→BD,D→EF}
step3: 分解右边,用假设法:
CE→FA,假设CE→F(CE)+=ACEF,能推出CE→A所以成立
CF→BD,假设CF→B (CF)+= BCDF,所以成立
D→EF,假设D→E,(D)+ = DE,假设D→F,(D)+=EF,不成立
综上:F c= {AB→C,C→A,BC→D,CD→B,BE→C,CE→F,CF→B,D→EF}
③最小覆盖Fm
Fm就是把Fc右端用分解率分开。