机器学习——支持向量机SVM学习总结
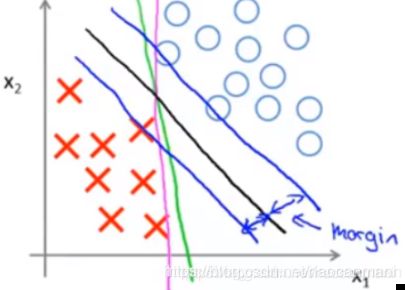
对于上图中的红叉和蓝圈,如果我们进行二分类,找到他的分类边界,那么有许多中可能(绿色,粉色,黑色)。但是,绿色和粉色的分类超平面,对于未知样本的预测效果会比黑色的差。支持向量机,就是去找到这样一个分类超平面,使得样本点到这个平面的距离最大。
数学模型
判别模型 f ( x ) = w T x + b f(x)=w^Tx+b f(x)=wTx+b,把b当成w的一部分则 f ( x ) = w T x f(x)=w^Tx f(x)=wTx,对于最大间隔,要满足以下式子:
m a x m a r g i n ( w , b ) s . t . y i ( w T x i + b ) > 0 max \space margin(w, b)\\s.t. y_i(w^Tx_i+b)>0 max margin(w,b)s.t.yi(wTxi+b)>0
m a r g i n ( w , b ) = min w , b , x i d i s t a n c e ( w , b , x i ) min w , b , x i ∣ w T x i + b ∣ ∣ ∣ w ∣ ∣ ( 1 ) margin(w,b)=\min_{w,b,x_i}~distance(w,b,x_i) \\ \min_{w,b,x_i}\frac{|w^Tx_i+b|}{||w||}~~~~~(1) margin(w,b)=w,b,ximin distance(w,b,xi)w,b,ximin∣∣w∣∣∣wTxi+b∣ (1)
(1)式为点到直线的距离
对于分类问题:
w T x + b > 0 y = 1 w T x + b < = 0 y = − 1 w^Tx+b>0~~~y=1 \\ w^Tx+b<=0~~~y=-1 wTx+b>0 y=1wTx+b<=0 y=−1
因此 ∣ w T x i + b ∣ |w^Tx_i+b| ∣wTxi+b∣可以转换成 y i ( w T x i + b ) y_i(w^Tx_i+b) yi(wTxi+b),
max w , b min x i ∣ w T x i + b ∣ ∣ ∣ w ∣ ∣ = max w , b 1 ∣ ∣ w ∣ ∣ min x i y ( w T x i + b ) s . t . y ( w T x i + b ) > 0 \max_{w,b}\min_{x_i} \frac{|w^Tx_i+b|}{||w||} = \max_{w,b}\frac{1}{||w||}\min_{x_i} y(w^Tx_i+b) \\ s.t.y(w^Tx_i+b)>0 w,bmaxximin∣∣w∣∣∣wTxi+b∣=w,bmax∣∣w∣∣1ximiny(wTxi+b)s.t.y(wTxi+b)>0
对于 min x i y ( w T x i + b ) \min_{x_i} y(w^Tx_i+b) minxiy(wTxi+b),一定存在一个R 使得 min x y ( w T x + b ) = R \min_{x} y(w^Tx+b)=R minxy(wTx+b)=R
对于R可以进行缩放,比如x=1和2x=2其实表达是一样的,因此这里就直接假设R=1, min x y ( w T x + b ) = R \min_{x} y(w^Tx+b)=R minxy(wTx+b)=R等价于 y ( w T x + b ) > = R y(w^Tx+b)>=R y(wTx+b)>=R
则上式为:
max w , b 1 ∣ ∣ w ∣ ∣ s . t . y i ( w T x i + b ) > = 1 \max_{w,b}\frac{1}{||w||} \\ s.t.y_i(w^Tx_i+b)>=1 w,bmax∣∣w∣∣1s.t.yi(wTxi+b)>=1
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 s . t . y i ( w T x i + b ) > = 1 ( 2 ) \min_{w,b}\frac{1}{2}||w||^2 \\ s.t.y_i(w^Tx_i+b)>=1~~~(2) w,bmin21∣∣w∣∣2s.t.yi(wTxi+b)>=1 (2)
对maxmin的解释:
min是求样本中离直线最近的点,这些点可以理解为支持向量
max使得这些最近的点到分类超平面的距离最大
对偶问题
对于上面的式子,是一个
凸二次规划问题,可以直接用相应的方法求解,但是遇到维度较高的情况时,就不能直接用二次规划的方法做,因此这里引入他的对偶问题。
拉格朗日乘子法
对于上式改写为:
L ( w , b , λ ) = 1 2 w T w + ∑ i = 1 N λ i ( 1 − y i ( w T x i + b ) ) s . t . λ i > = 0 L(w,b,\lambda)=\frac{1}{2}w^Tw+\sum_{i=1}^N{\lambda_i(1-y_i(w^Tx_i+b))} \\ s.t.\lambda_i>=0 L(w,b,λ)=21wTw+i=1∑Nλi(1−yi(wTxi+b))s.t.λi>=0
min w , b max λ L s . t . λ i > = 0 \min_{w,b}\max_{\lambda}L \\ s.t.\lambda_i>=0 w,bminλmaxLs.t.λi>=0
拉格朗日乘子法中: L ( w , b , λ ) = h ( x ) + ∑ i = 1 N λ i g ( x ) L(w,b,\lambda)=h(x)+\sum_{i=1}^N{\lambda_i g(x)} L(w,b,λ)=h(x)+∑i=1Nλig(x) λ \lambda λ大于等于0,g(x)小于等于0
对偶关系:minmax <= maxmin即最大值中的最小值肯定大于等于最小值中的最大值。而对于凸二次规划问题,满足强对偶关系,即minmax=maxmin
所以原式可以转换为
max λ min w , b L s . t . λ > = 0 \max_{\lambda}\min_{w,b}L \\ s.t.\lambda>=0 λmaxw,bminLs.t.λ>=0
对于min是不受lambda约束的,所以可以直接求解。求出L关于w,b的偏导数,然后带入L得到 max λ P λ > = 0 \max_{\lambda}P \\ \lambda >= 0 λmaxPλ>=0
P的表达式:
w ∗ = ∑ i = 1 N λ i y i x i w^*=\sum_{i=1}^N{\lambda_iy_ix_i} w∗=∑i=1Nλiyixi, b ∗ = ∑ i = 1 N λ i y i b^*=\sum_{i=1}^N{\lambda_iy_i} b∗=∑i=1Nλiyi
P = min λ ∑ i = 1 N ∑ j = 1 N λ i λ j y i y j x i T x j − ∑ i N λ i s . t . λ > = 0 ∑ i = 1 N λ i y i = 0 P=\min_{\lambda}\sum_{i=1}^N{\sum_{j=1}^N{\lambda_i\lambda_jy_iy_jx_i^Tx_j}}-\sum_{i}^N{\lambda_i} \\ s.t.\lambda>=0 \\ \sum_{i=1}^N{\lambda_iy_i}=0 P=λmini=1∑Nj=1∑NλiλjyiyjxiTxj−i∑Nλis.t.λ>=0i=1∑Nλiyi=0
对于凸二次规划问题,前面提到他一定是满足强对偶关系的,而他的充要条件就是满足KKT条件。
KKT条件:
f ( x ) = { λ > = 0 1 − y ( w T x + b ) < = 0 λ ( 1 − y ( w T x + b ) ) = 0 w ∗ , b ∗ , λ ∗ = 0 f(x)=\left\{ \begin{aligned} \lambda&>=&0 \\ 1-y(w^Tx+b)&<=&0\\ \lambda(1-y(w^Tx+b))&=&0 \\ w^*,b^*,\lambda^*&=&0 \end{aligned} \right. f(x)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧λ1−y(wTx+b)λ(1−y(wTx+b))w∗,b∗,λ∗>=<===0000
w ∗ , b ∗ , λ ∗ w^*,b^*,\lambda^* w∗,b∗,λ∗是导数,直观上理解,对于L,想要得到最大值就得后半部分为0,最大值为 1 2 w T w \frac{1}{2}w^Tw 21wTw。而后半部分为0,那就是 λ \lambda λ为0或者 1 − y ( w T x + b ) 1-y(w^Tx+b) 1−y(wTx+b)为0。
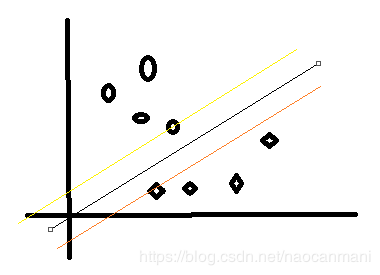
对于在黄色和橙色线上的点 1 − y ( w T x + b ) 1-y(w^Tx+b) 1−y(wTx+b)为0,而在两条线以外的点则 1 − y ( w T x + b ) < 0 1-y(w^Tx+b)<0 1−y(wTx+b)<0因此此时 λ = 0 \lambda=0 λ=0
w ∗ = ∑ i = 1 N λ i y i x i w^*=\sum_{i=1}^N{\lambda_iy_ix_i} w∗=∑i=1Nλiyixi
一定存在一个 ( x k , y k ) (x_k,y_k) (xk,yk)使得 w T x k + b = y k w^Tx_k+b=y_k wTxk+b=yk,即在两条彩色线上。
b ∗ = y k − w T x k = y k − ∑ i = 1 N y i x i T x k b^*=y_k-w^Tx_k=y_k-\sum_{i=1}^N{y_ix_i^Tx_k} b∗=yk−wTxk=yk−∑i=1NyixiTxk
分类超平面为 w ∗ T x + b ∗ w^{*T}x+b^* w∗Tx+b∗
以上是hard margin的情况,也就是假设样本在理想情况下是完全可以被分开的,没有噪声的,下面总结一下soft margin的知识
soft margin
字面上理解就是相对hard,soft的条件没有这么苛刻,允许一点点错误。
所谓的一点点错误,用loss来表示,我们可以用01损失来表达,即loss表示违反条件(超过红色线)的个数 ∑ i = 1 N I { y i ( w T x i + b ) < 1 } \sum_{i=1}^N{I\{y_i(w^Tx_i+b)<1\}} ∑i=1NI{yi(wTxi+b)<1},I表示个数
但是01loss是不连续的,求导不好弄,因此对其进行改进。
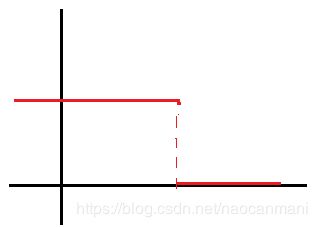
改进后
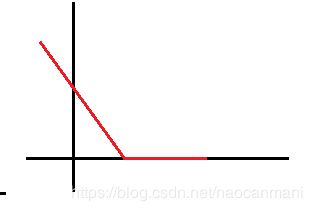
采用hinge loss 在满足条件的时候( y i ( w T x i + b ) > = 1 y_i(w^Tx_i+b)>=1 yi(wTxi+b)>=1)就为0,不满足的时候就等于
1 − y i ( w T x i + b ) 1- y_i(w^Tx_i+b) 1−yi(wTxi+b)
l o s s = max { 0 , 1 − y i ( w T x i + b ) } loss=\max\{0, 1-y_i(w^Tx_i+b)\} loss=max{0,1−yi(wTxi+b)}
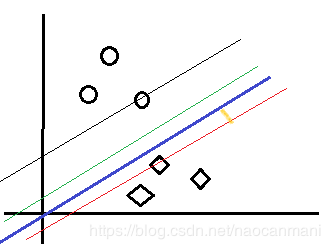
ξ \xi ξ来表示loss,可得 ξ > = 0 \xi>=0 ξ>=0
如上图所示,蓝色的线就是使用soft margin后的情况,允许在黄色这段区间内存在一些噪声。
式(2可以写成)
min w , b 1 2 w T w + C ∑ i = 1 N ξ i s . t . y i ( w T x i + b ) > = 1 − ξ i \min_{w,b}\frac{1}{2}w^Tw+C\sum_{i=1}^N{\xi_i}\\ s.t.y_i(w^Tx_i+b)>=1-\xi_i w,bmin21wTw+Ci=1∑Nξis.t.yi(wTxi+b)>=1−ξi
C是系数
参考:https://www.bilibili.com/video/BV1Hs411w7ci?p=3