FaceShifter: Towards High Fidelity And Occlusion Aware Face Swapping
3. Methods
定义 X s X_s Xs为source image,提供identity信息, X t X_t Xt为target image,提供attribute信息(包括pose、expression、scene lighting和background)
FaceShifter包含2个stage,在stage1中,采用Adaptive Embedding Integration Network(AEI-Net)生成high fidelity face swapping result Y ^ s , t \hat{Y}_{s,t} Y^s,t;在stage2中,采用Heuristic Error Acknowledging Network((HEAR-Net)处理脸部的遮挡问题,进一步生成更精细的结果 Y s , t Y_{s,t} Ys,t
3.1. Adaptive Embedding Integration Network
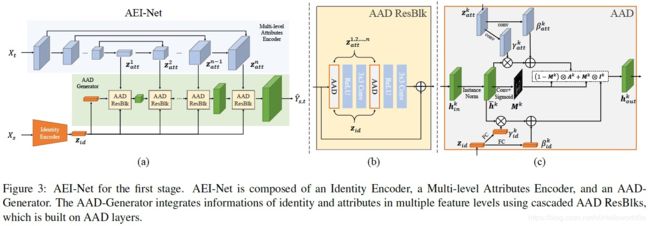
如Figure 3(a)所示,stage1的网络结构包含3个部分
- the Idenitty Encoder z i d ( X s ) \bm{z}_{id}(X_s) zid(Xs)(橙色部分),用于提取identity信息
- the Multi-level Attributes Encoder z a t t ( X t ) \bm{z}_{att}(X_t) zatt(Xt)(灰色部分),用于提取attrubute信息
- Adaptive Attentional Denormalization (AAD) Generator(绿色部分),结合identity和attribute信息,生成换脸结果
Identity Encoder
采用最新的人脸识别模型(来自文献[13]),取the last feature vector generated before the final FC layer作为identity embedding
Multi-level Attributes Encoder
Face attributes, such as pose, expression, lighting and background, require more spatial informations than identity.
为了保存attribute信息,取multi-level feature maps作为attribute embedding(之前的工作将attribute信息压缩为single vector)
具体来说,将 X t X_t Xt送入类似U-Net的网络,然后收集decoder部分每一层的feature map作为 z a t t ( X t ) z_{att}(X_t) zatt(Xt)
z a t t ( X t ) = { z a t t 1 ( X t ) , z a t t 2 ( X t ) , ⋯ , z a t t n ( X t ) } ( 1 ) \bm{z}_{att}(X_t)=\left \{ \bm{z}_{att}^1(X_t), \bm{z}_{att}^2(X_t), \cdots, \bm{z}_{att}^n(X_t) \right \} \qquad(1) zatt(Xt)={zatt1(Xt),zatt2(Xt),⋯,zattn(Xt)}(1)
其中 z a t t k ( X t ) \bm{z}_{att}^k(X_t) zattk(Xt)表示U-Net decoder第k层输出的feature map
值得注意的是,Multi-level Attributes Encoder不需要attribute annotation,能够通过self-supervised training的方式自动提取attribute信息
定义了attribute embedding之后,我们希望换脸结果 Y ^ x t \hat{Y}_{x_t} Y^xt与target image X t X_t Xt有相同的attribute embedding
Adaptive Attentional Denormalization Generator
这一步将2个embedding z i d ( X s ) \bm{z}_{id}(X_s) zid(Xs)和 z a t t ( X t ) \bm{z}_{att}(X_t) zatt(Xt)整合起来,用于生成换脸结果 Y ^ s , t \hat{Y}_{s,t} Y^s,t
之前的工作采用feature concatenation,会生成模糊的结果,因此我们提出Adaptive Attentional Denormalization(AAD),采用adaptive fashion的思想来解决这个问题
定义 h i n k \bm{h}_{in}^k hink表示AAD layer的输入,首先对 h i n k \bm{h}_{in}^k hink,进行instance normalization
h ˉ k = h i n k − μ k σ k ( 2 ) \bar{\bm{h}}_k=\frac{\bm{h}_{in}^k-\bm{\mu}^k}{\bm{\sigma}^k} \qquad(2) hˉk=σkhink−μk(2)
第一步,attributes embedding integration
ADD layer接收 z a t t k ∈ R C a t t k × H k × W k \bm{z}_{att}^k\in\mathbb{R}^{C_{att}^k\times H^k\times W^k} zattk∈RCattk×Hk×Wk作为输入,然后对 z a t t k \bm{z}_{att}^k zattk进行卷积得到 γ a t t k , β a t t k ∈ R C k × H k × W k \gamma_{att}^k, \beta_{att}^k\in\mathbb{R}^{C^k\times H^k\times W^k} γattk,βattk∈RCk×Hk×Wk
然后利用 γ a t t k , β a t t k \gamma_{att}^k, \beta_{att}^k γattk,βattk对normalized h ˉ k \bar{\bm{h}}_k hˉk进行denormalization,得到attribute activation A k \bm{A}^k Ak
A k = γ a t t k ⊗ h ˉ k + β a t t k ( 3 ) \bm{A}^k=\gamma_{att}^k\otimes\bar{\bm{h}}_k+\beta_{att}^k \qquad(3) Ak=γattk⊗hˉk+βattk(3)
第二步,identity embedding integration
从 X s X_s Xs中提取identity embedding z i d k \bm{z}_{id}^k zidk,然后对 z i d k \bm{z}_{id}^k zidk进行FC得到 γ i d k , β i d k ∈ R C k \gamma_{id}^k, \beta_{id}^k\in\mathbb{R}^{C^k} γidk,βidk∈RCk
以同样的方式对normalized h ˉ k \bar{\bm{h}}_k hˉk进行denormalization,得到identity activation I k \bm{I}^k Ik
I k = γ i d k ⊗ h ˉ k + β i d k ( 4 ) \bm{I}^k=\gamma_{id}^k\otimes\bar{\bm{h}}_k+\beta_{id}^k \qquad(4) Ik=γidk⊗hˉk+βidk(4)
第三步,adaptively attention mask
对 h ˉ k \bar{\bm{h}}_k hˉk进行conv+sigmoid运算,学习一个attentional mask M k \bm{M}^k Mk,最终利用 M k \bm{M}^k Mk对 A k \bm{A}^k Ak和 I k \bm{I}^k Ik进行组合
h o u t k = ( 1 − M k ) ⊗ A k + M k ⊗ I k ( 5 ) \bm{h}_{out}^k=\left ( 1-\bm{M}^k \right )\otimes\bm{A}^k+\bm{M}^k\otimes\bm{I}^k \qquad(5) houtk=(1−Mk)⊗Ak+Mk⊗Ik(5)
Figure 3 ( c)展示的就是上述所说的三步操作,然后将多个AAD layer组合起来,得到AAD ResBlk,如Figure 3(b)所示
Training Losses
首先设置multi-scale discriminator,得到adversarial loss L a d v \mathcal{L}_{adv} Ladv
然后定义identity preservation loss L i d \mathcal{L}_{id} Lid
L i d = 1 − c o s ( z i d ( Y ^ s , t ) , z i d ( X s ) ) ( 6 ) \mathcal{L}_{id}=1-cos\left ( \bm{z}_{id}\left ( \hat{Y}_{s,t} \right ), \bm{z}_{id}\left ( X_s \right ) \right ) \qquad(6) Lid=1−cos(zid(Y^s,t),zid(Xs))(6)
接着定义attributes preservation loss L a t t \mathcal{L}_{att} Latt
L a t t = 1 2 ∑ k = 1 n ∥ z a t t k ( Y ^ s , t ) − z a t t k ( X t ) ∥ 2 2 ( 8 ) \mathcal{L}_{att}=\frac{1}{2}\sum_{k=1}^{n}\left \| \bm{z}_{att}^k\left ( \hat{Y}_{s,t} \right ) - \bm{z}_{att}^k\left ( X_t \right ) \right \|_2^2 \qquad(8) Latt=21k=1∑n∥∥∥zattk(Y^s,t)−zattk(Xt)∥∥∥22(8)
在训练过程中以80%的比例令 X t = X s X_t=X_s Xt=Xs,则定义reconstruction loss L r e c \mathcal{L}_{rec} Lrec如下
L r e c = { 1 2 ∥ Y ^ s , t − X t ∥ 2 2 if X t = X s 0 otherwise ( 8 ) \mathcal{L}_{rec}=\left\{\begin{matrix} \frac{1}{2}\left \| \hat{Y}_{s,t}-X_t \right \|_2^2 & \text{if}\ X_t=X_s\\ 0 & \text{otherwise} \end{matrix}\right. \qquad(8) Lrec={21∥∥∥Y^s,t−Xt∥∥∥220if Xt=Xsotherwise(8)
对于AEI-NET,完整的损失函数如下
L A E I − N e t = L a d v + λ a t t L a t t + λ i d L i d + λ r e c L r e c ( 9 ) \mathcal{L}_{{\rm AEI-Net}}=\mathcal{L}_{adv}+\lambda_{att}\mathcal{L}_{att}+\lambda_{id}\mathcal{L}_{id}+\lambda_{rec}\mathcal{L}_{rec} \qquad(9) LAEI−Net=Ladv+λattLatt+λidLid+λrecLrec(9)
其中设置 λ a t t = λ r e c = 10 \lambda_{att}=\lambda_{rec}=10 λatt=λrec=10, λ i d = 5 \lambda_{id}=5 λid=5
3.2. Heuristic Error Acknowledging Refinement Network
stage1生成的图像能够很好的保持target attributes,但无法保持来自 X t X_t Xt中的遮挡(occlusion)
已有的工作额外训练一个face segmentation network,缺点是需要occlusion annotation,并且对于新的occlusion的泛化性不好

在实验中, X t X_t Xt是一幅包含occlusion的图像,令 X s = X t X_s=X_t Xs=Xt,重构的图像为 Y ^ t t = A E I - N e t ( X t , X t ) \hat{Y}_{tt}={\rm AEI\text{-}Net}(X_t, X_t) Y^tt=AEI-Net(Xt,Xt),我们观察到 Y ^ t t \hat{Y}_{tt} Y^tt本该重构出来的occlusion消失了,于是将 Y ^ t t \hat{Y}_{tt} Y^tt与 X t X_t Xt进行比对,可以得知图像中哪些地方是occlusion
定义heuristic error如下
Δ Y t = X t − A E I - N e t ( X t , X t ) ( 10 ) \Delta Y_t=X_t-{\rm AEI\text{-}Net}(X_t, X_t) \qquad(10) ΔYt=Xt−AEI-Net(Xt,Xt)(10)
如Figure 4(b)所示,HEAR-Net本质上是一个U-Net,接收 Δ Y t \Delta Y_t ΔYt和 Y ^ s , t \hat{Y}_{s,t} Y^s,t作为输入,输出最终的换脸结果 Y s , t Y_{s,t} Ys,t
Y s , t = H E A R - N e t ( Y ^ s , t , Δ Y t ) ( 11 ) Y_{s,t}={\rm HEAR\text{-}Net}\left ( \hat{Y}_{s,t}, \Delta Y_t \right ) \qquad(11) Ys,t=HEAR-Net(Y^s,t,ΔYt)(11)
训练HEAR-Net的损失项包含3项
第1项是the identity preservation loss L i d ′ \mathcal{L}_{id}' Lid′
L i d ′ = 1 − c o s ( z i d ( Y s , t ) , z i d ( X s ) ) ( 12 ) \mathcal{L}_{id}'=1-cos\left ( \bm{z}_{id}\left ( Y_{s,t} \right ), \bm{z}_{id}\left ( X_s \right ) \right ) \qquad(12) Lid′=1−cos(zid(Ys,t),zid(Xs))(12)
第2项是the change loss L c h g ′ \mathcal{L}_{chg}' Lchg′
L c h g ′ = ∣ Y ^ s , t − Y s , t ∣ ( 13 ) \mathcal{L}_{chg}'=\left | \hat{Y}_{s,t}-Y_{s,t} \right | \qquad(13) Lchg′=∣∣∣Y^s,t−Ys,t∣∣∣(13)
第3项是the reconstruction loss L r e c ′ \mathcal{L}_{rec}' Lrec′
L r e c ′ = { 1 2 ∥ Y s , t − X t ∥ 2 2 if X t = X s 0 otherwise ( 14 ) \mathcal{L}_{rec}'=\left\{\begin{matrix} \frac{1}{2}\left \| Y_{s,t}-X_t \right \|_2^2 & \text{if}\ X_t=X_s\\ 0 & \text{otherwise} \end{matrix}\right. \qquad(14) Lrec′={21∥Ys,t−Xt∥220if Xt=Xsotherwise(14)
总体的损失函数为三者之和
L H E A R - N e t = L r e c ′ + L i d ′ + L c h g ′ ( 15 ) \mathcal{L}_{{\rm HEAR\text{-}Net}}=\mathcal{L}_{rec}'+\mathcal{L}_{id}'+\mathcal{L}_{chg}' \qquad(15) LHEAR-Net=Lrec′+Lid′+Lchg′(15)