PTA_PAT甲级_1018 Public Bike Management (30分)

There is a public bike service in Hangzhou City which provides great convenience to the tourists from all over the world. One may rent a bike at any station and return it to any other stations in the city.

The Public Bike Management Center (PBMC) keeps monitoring the real-time capacity of all the stations. A station is said to be in perfect condition if it is exactly half-full. If a station is full or empty, PBMC will collect or send bikes to adjust the condition of that station to perfect. And more, all the stations on the way will be adjusted as well.

When a problem station is reported, PBMC will always choose the shortest path to reach that station. If there are more than one shortest path, the one that requires the least number of bikes sent from PBMC will be chosen.

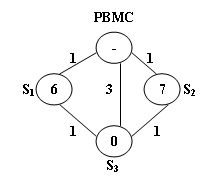
The above figure illustrates an example. The stations are represented by vertices and the roads correspond to the edges. The number on an edge is the time taken to reach one end station from another. The number written inside a vertex S is the current number of bikes stored at S. Given that the maximum capacity of each station is 10. To solve the problem at S​3, we have 2 different shortest paths:

PBMC -> S1-> S3. In this case, 4 bikes must be sent from PBMC, because we can collect 1 bike from S1 and then take 5 bikes to S3, so that both stations will be in perfect conditions.

PBMC -> S​2-> S3. This path requires the same time as path 1, but only 3 bikes sent from PBMC and hence is the one that will be chosen.

Input Specification:
Each input file contains one test case. For each case, the first line contains 4 numbers: Cmax(≤100), always an even number, is the maximum capacity of each station; N (≤500), the total number of stations; Sp, the index of the problem station (the stations are numbered from 1 to N, and PBMC is represented by the vertex 0); and M, the number of roads. The second line contains N non-negative numbers C​i(i=1,⋯,N) where each C​i is the current number of bikes at Si respectively. Then M lines follow, each contains 3 numbers: S​i, S​j, and T​ij which describe the time T​ij​​ taken to move betwen stations S​i and S​j. All the numbers in a line are separated by a space.

Output Specification:
For each test case, print your results in one line. First output the number of bikes that PBMC must send. Then after one space, output the path in the format: 0−>S​1−>⋯−>S​p. Finally after another space, output the number of bikes that we must take back to PBMC after the condition of S​p is adjusted to perfect.

Note that if such a path is not unique, output the one that requires minimum number of bikes that we must take back to PBMC. The judge’s data guarantee that such a path is unique.

Sample Input:

10 3 3 5
6 7 0
0 1 1
0 2 1
0 3 3
1 3 1
2 3 1

Sample Output:

3 0->2->3 0

题意：
每个车站有一定容量，完美状态是半满，从起点到问题站点经过的站点都必须调整到完美状态，求距离最短且需要携带和带回的自行车数最少的路径

分析：
使用Dijkstra+DFS，不能只用Dijkstra，因为minNeed和minRemain在路径上的传递不满足最优子结构（不是简单的相加过程）

代码：

#include
#include
#include
#include
#include
using namespace std;

#define MAXV 510
#define INF 1e9
int N, M, Cmax, Sp, numPath=0, G[MAXV][MAXV], weight[MAXV];
int d[MAXV], minNeed=INF, minRemain=INF, vis[MAXV]={0};
vector<int> pre[MAXV], tmpPath, path;//前驱，临时路径，最优路径

void Dijkstra(int s);
void DFS(int v);

int main()
{
	cin>>Cmax>>N>>Sp>>M;
	fill(G[0], G[0]+MAXV*MAXV, INF);
	for(int i=1;i<=N;i++){
		cin>>weight[i];
		weight[i] -= Cmax/2;//减去最大值的一半即可根据正负判断是否需要补充或带走
	}
	for(int i=0;i<M;i++){
		int u,v;
		cin>>u>>v;
		cin>>G[u][v];//必须和上一步分开写
		G[v][u] = G[u][v];
	}	
	Dijkstra(0);
	DFS(Sp);
	cout<<minNeed<<" ";
	for(int i=path.size()-1;i>=0;i--){
		cout<<path[i];
		if(i>0) cout<<"->";
	}
	cout<<" "<<minRemain;
	return 0;
} 

void Dijkstra(int s){
	fill(d, d+MAXV, INF);
	d[s] = 0;
	for(int i=0;i<=N;i++){//循环N+1次 
		int u=-1,MIN=INF;//u使d[u]最小，MIN存放该最小的d[u]
		for(int j=0;j<=N;j++){//找到未访问的顶点中d[]最小的
			if(vis[j]==0 && d[j]<MIN){
				u = j;
				MIN = d[j];
			}
		}
		if(u==-1) return;//说明剩下的顶点和s不连通
		vis[u] = 1;
		for(int v=0;v<=N;v++){
			if(vis[v]==0 && G[u][v]!=INF){//对u的每个未访问的邻接点
				if(d[u]+G[u][v]<d[v]){
					d[v] = d[u] + G[u][v];
					pre[v].clear();
					pre[v].push_back(u);
				}else if(d[u]+G[u][v]==d[v]) pre[v].push_back(u);
			}
		} 
	}
}

void DFS(int v){
	if(v==0){//递归边界，叶子节点
		tmpPath.push_back(v);
		int need=0, remain=0;
		for(int i=tmpPath.size()-1;i>=0;i--){//必须倒着枚举//这样才能得到在起点的数量
			int id = tmpPath[i];
			if(weight[id]>0) remain += weight[id];//点权大于0说明需要带走
			else{//否则需要补给
				if(remain>abs(weight[id])) remain -= abs(weight[id]);//当前持有量足够补给
				else{//否则需要从PBMC携带
					need += abs(weight[id]) - remain;
					remain = 0;
				}
			}
		}
		if(need<minNeed){//需要从PBMC携带的数量更少则更新
			minNeed = need;
			minRemain = remain;
			path = tmpPath;
		}else if(need==minNeed && remain<minRemain){//携带数目相同但带回数目变少也更新
			minRemain = remain;
			path = tmpPath;
		}
		tmpPath.pop_back();
		return;
	}
	tmpPath.push_back(v);
	for(int i=0;i<pre[v].size();i++)
		DFS(pre[v][i]);
	tmpPath.pop_back();
}