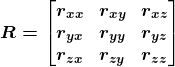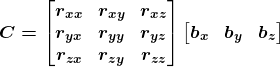一、什么是宏函数?通过宏定义的函数是宏函数。如下,编译器在预处理阶段会将Add(x,y)替换为((x)*(y))#defineAdd(x,y)((x)*(y))#defineAdd(x,y)((x)*(y))intmain(){inta=10;intb=20;intd=10;intc=Add(a+d,b)*2;cout<
C语言如何定义宏函数?
小九格物
c语言
在C语言中,宏函数是通过预处理器定义的,它在编译之前替换代码中的宏调用。宏函数可以模拟函数的行为,但它们不是真正的函数,因为它们在编译时不会进行类型检查,也不会分配存储空间。宏函数的定义通常使用#define指令,后面跟着宏的名称和参数列表,以及宏展开后的代码。宏函数的定义方式:1.基本宏函数:这是最简单的宏函数形式,它直接定义一个表达式。#defineSQUARE(x)((x)*(x))2.带参
学点心理知识,呵护孩子健康
静候花开_7090
昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所,超越教育与技术的思考》的讲座。今天又重新学习了一遍,收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题,她说心理健康的一些基本命题,我们与我们通常的一些教育命题是不同的,她还举了几个例子,让我们明白我们原来以为的健康并非心理学上的健康。比如如果
Linux下QT开发的动态库界面弹出操作(SDL2)
13jjyao
QT类qt开发语言sdl2linux
需求:操作系统为linux,开发框架为qt,做成需带界面的qt动态库,调用方为java等非qt程序难点:调用方为java等非qt程序,也就是说调用方肯定不带QApplication::exec(),缺少了这个,QTimer等事件和QT创建的窗口将不能弹出(包括opencv也是不能弹出);这与qt调用本身qt库是有本质的区别的思路:1.调用方缺QApplication::exec(),那么我们在接口
ArcGIS栅格计算器常见公式(赋值、0和空值的转换、补充栅格空值)
研学随笔
arcgis经验分享
我们在使用ArcGIS时通常经常用到栅格计算器,今天主要给大家介绍我日常中经常用到的几个公式,供大家参考学习。将特定值(-9999)赋值为0,例如-9999.Con("raster"==-9999,0,"raster")2.给空值赋予特定的值(如0)Con(IsNull("raster"),0,"raster")3.将特定的栅格值(如1)赋值为空值,其他保留原值SetNull("raster"==
【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数
广龙宇
一起学Rust#Rust设计模式rust设计模式开发语言
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言,它的所有特性,使其独一无二。因此,学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此,本系列文章的结构也与此书的结构相同(后续可能会调成结构),基本上分为三个部分
回溯 Leetcode 332 重新安排行程
mmaerd
Leetcode刷题学习记录leetcode算法职场和发展
重新安排行程Leetcode332学习记录自代码随想录给你一份航线列表tickets,其中tickets[i]=[fromi,toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从JFK(肯尼迪国际机场)出发的先生,所以该行程必须从JFK开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。例如,行程[“JFK”,“LGA”]与[“JFK”,“LGB
Python数据分析与可视化实战指南
William数据分析
pythonpython数据
在数据驱动的时代,Python因其简洁的语法、强大的库生态系统以及活跃的社区,成为了数据分析与可视化的首选语言。本文将通过一个详细的案例,带领大家学习如何使用Python进行数据分析,并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前,我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
每日一题——第八十四题
互联网打工人no1
C语言程序设计每日一练c语言
题目:编写函数1、输入10个职工的姓名和职工号2、按照职工由大到小顺序排列,姓名顺序也随之调整3、要求输入一个职工号,用折半查找法找出该职工的姓名#define_CRT_SECURE_NO_WARNINGS#include#include#defineMAX_EMPLOYEES10typedefstruct{intid;charname[50];}Empolyee;voidinputEmploye
2019-12-22-22:30
涓涓1016
今天是冬至,写下我的日更,是因为这两天的学习真的是能量的满满,让我看到了自己,未来另外一种可能性,也让我看到了这两年这几年的过程中我所接受那些痛苦的来源。一切的根源和痛苦都来自于人生,家庭,而你的原生家庭,你的爸爸和妈妈,是因为你这个灵魂在那一刻选择他们作为你的爸爸和妈妈来的,所以你得接受他,你得接纳他,他就是因为他的存在而给你的学习和成长带来这些痛苦,那其实是你必然要经历的这个过程,当你去接纳的
Python教程:一文了解使用Python处理XPath
旦莫
Python进阶python开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath?2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
将cmd中命令输出保存为txt文本文件
落难Coder
Windowscmdwindow
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码,无可厚非,我们有必要保存我们的炼丹结果,但是复制命令行输出到txt是非常麻烦的,其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是:运行指令>输出到的文件名称或者具体保存路径测试下,我打开cmd并且ping一下百度:pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出:如果你再
四章-32-点要素的聚合
彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记,使用的openlayers5.3.xapi。源码见1032.html,对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
GitHub上克隆项目
bigbig猩猩
github
从GitHub上克隆项目是一个简单且直接的过程,它允许你将远程仓库中的项目复制到你的本地计算机上,以便进行进一步的开发、测试或学习。以下是一个详细的步骤指南,帮助你从GitHub上克隆项目。一、准备工作1.安装Git在克隆GitHub项目之前,你需要在你的计算机上安装Git工具。Git是一个开源的分布式版本控制系统,用于跟踪和管理代码变更。你可以从Git的官方网站(https://git-scm.
HTML网页设计制作大作业(div+css) 云南我的家乡旅游景点 带文字滚动
二挡起步
web前端期末大作业web设计网页规划与设计htmlcssjavascriptdreamweaver前端
Web前端开发技术描述网页设计题材,DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作HTML期末大学生网页设计作业HTML:结构CSS:样式在操作方面上运用了html5和css3,采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScript:做与用户的交互行为文章目录前端学习路线
Day17笔记-高阶函数
~在杰难逃~
Python笔记python开发语言pycharm数据分析
高阶函数【重点掌握】函数的本质:函数是一个变量,函数名是一个变量名,一个函数可以作为另一个函数的参数或返回值使用如果A函数作为B函数的参数,B函数调用完成之后,会得到一个结果,则B函数被称为高阶函数常用的高阶函数:map(),reduce(),filter(),sorted()1.map()map(func,iterable),返回值是一个iterator【容器,迭代器】func:函数iterab
Day1笔记-Python简介&标识符和关键字&输入输出
~在杰难逃~
Pythonpython开发语言大数据数据分析数据挖掘
大家好,从今天开始呢,杰哥开展一个新的专栏,当然,数据分析部分也会不定时更新的,这个新的专栏主要是讲解一些Python的基础语法和知识,帮助0基础的小伙伴入门和学习Python,感兴趣的小伙伴可以开始认真学习啦!一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码,再通过语言处理程序执行向计算机发送指令,让计算机完成对应的工作,编程
人工智能时代,程序员如何保持核心竞争力?
jmoych
人工智能
随着AIGC(如chatgpt、midjourney、claude等)大语言模型接二连三的涌现,AI辅助编程工具日益普及,程序员的工作方式正在发生深刻变革。有人担心AI可能取代部分编程工作,也有人认为AI是提高效率的得力助手。面对这一趋势,程序员应该如何应对?是专注于某个领域深耕细作,还是广泛学习以适应快速变化的技术环境?又或者,我们是否应该将重点转向AI无法轻易替代的软技能?让我们一起探讨程序员
Python快速入门 —— 第三节:类与对象
孤华暗香
Python快速入门python开发语言
第三节:类与对象目标:了解面向对象编程的基础概念,并学会如何定义类和创建对象。内容:类与对象:定义类:class关键字。类的构造函数:__init__()。类的属性和方法。对象的创建与使用。示例:classStudent:def__init__(self,name,age,major):self.name&#
node.js学习
小猿L
node.jsnode.js学习vim
node.js学习实操及笔记温故node.js,node.js学习实操过程及笔记~node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记为什么学node.js可以让别人访问我们编写的网页为后续的框架学习打下基础,三大框架vuereactangular离不开node.jsnode.js是什么官网:node.js是一个开源的、跨平台的运行JavaScript的运行
阶段总结反思
轻争
马上就要进入10月份了,今天做一下前段时间的总结和反思。前段时间,日更、英语、健身、护肤坚持的比较好。阅读、书法坚持的不好。1.中间被迫停更半个多月,其余时间一直在坚持日更挑战。偶尔也有不想写的时候,就做一下摘抄。因为阅读(输入)没跟上来,所以写作(输出)质量有待进一步加强。2.英语做到了一周至少学习5天,每次不少于30分钟,但是小班课没有跟上更新速度,下一步要争取利用零碎时间补听小班课。3.减肥
Python爬虫解析工具之xpath使用详解
eqa11
python爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中,数据提取是一个至关重要的环节。xpath作为一门
ARM驱动学习之基础小知识
JT灬新一
ARM嵌入式arm开发学习
ARM驱动学习之基础小知识•sch原理图工程师工作内容–方案–元器件选型–采购(能不能买到,价格)–原理图(涉及到稳定性)•layout画板工程师–layout(封装、布局,布线,log)(涉及到稳定性)–焊接的一部分工作(调试阶段板子的焊接)•驱动工程师–驱动,原理图,layout三部分的交集容易发生矛盾•PCB研发流程介绍–方案,原理图(网表)–layout工程师(gerber文件)–PCB板
ARM驱动学习之5 LEDS驱动
JT灬新一
嵌入式C底层arm开发学习单片机
ARM驱动学习之5LEDS驱动知识点:•linuxGPIO申请函数和赋值函数–gpio_request–gpio_set_value•三星平台配置GPIO函数–s3c_gpio_cfgpin•GPIO配置输出模式的宏变量–S3C_GPIO_OUTPUT注意点:DRIVER_NAME和DEVICE_NAME匹配。实现步骤:1.加入需要的头文件://Linux平台的gpio头文件#include//三
ARM驱动学习之4小结
JT灬新一
嵌入式C++arm开发学习linux
ARM驱动学习之4小结#include#include#include#include#include#defineDEVICE_NAME"hello_ctl123"MODULE_LICENSE("DualBSD/GPL");MODULE_AUTHOR("TOPEET");staticlonghello_ioctl(structfile*file,unsignedintcmd,unsignedlo
展现思维导图魅力,不断挖掘人生宝藏
思维导图讲师Mandy
第13期最强思维导图训练营已经结束一周了,但是我依旧是感觉所有学员还在努力的学习,这些学员中有教师、学生、白领、公务员、宝妈等等,只要你努力,只要你想改变自己,任何行业,任何岗位都可以参与进来,28天足以让你见成效,在这28天中,我们的学员不仅仅是收获了一枚毕业证,最重要的是让自己的思维方式得到升级,今天的你为自己投资,明天的你就会感谢你今天的付出,我们来听一听来自13期最强思维导图训练营优秀学员
对股票分析时要注意哪些主要因素?
会飞的奇葩猪
股票 分析 云掌股吧
众所周知,对散户投资者来说,股票技术分析是应战股市的核心武器,想学好股票的技术分析一定要知道哪些是重点学习的,其实非常简单,我们只要记住三个要素:成交量、价格趋势、振荡指标。
一、成交量
大盘的成交量状态。成交量大说明市场的获利机会较多,成交量小说明市场的获利机会较少。当沪市的成交量超过150亿时是强市市场状态,运用技术找综合买点较准;
【Scala十八】视图界定与上下文界定
bit1129
scala
Context Bound,上下文界定,是Scala为隐式参数引入的一种语法糖,使得隐式转换的编码更加简洁。
隐式参数
首先引入一个泛型函数max,用于取a和b的最大值
def max[T](a: T, b: T) = {
if (a > b) a else b
}
因为T是未知类型,只有运行时才会代入真正的类型,因此调用a >
C语言的分支——Object-C程序设计阅读有感
darkblue086
applec框架cocoa
自从1972年贝尔实验室Dennis Ritchie开发了C语言,C语言已经有了很多版本和实现,从Borland到microsoft还是GNU、Apple都提供了不同时代的多种选择,我们知道C语言是基于Thompson开发的B语言的,Object-C是以SmallTalk-80为基础的。和C++不同的是,Object C并不是C的超集,因为有很多特性与C是不同的。
Object-C程序设计这本书
去除浏览器对表单值的记忆
周凡杨
html记忆autocompleteform浏览
&n
java的树形通讯录
g21121
java
最近用到企业通讯录,虽然以前也开发过,但是用的是jsf,拼成的树形,及其笨重和难维护。后来就想到直接生成json格式字符串,页面上也好展现。
// 首先取出每个部门的联系人
for (int i = 0; i < depList.size(); i++) {
List<Contacts> list = getContactList(depList.get(i
Nginx安装部署
510888780
nginxlinux
Nginx ("engine x") 是一个高性能的 HTTP 和 反向代理 服务器,也是一个 IMAP/POP3/SMTP 代理服务器。 Nginx 是由 Igor Sysoev 为俄罗斯访问量第二的 Rambler.ru 站点开发的,第一个公开版本0.1.0发布于2004年10月4日。其将源代码以类BSD许可证的形式发布,因它的稳定性、丰富的功能集、示例配置文件和低系统资源
java servelet异步处理请求
墙头上一根草
java异步返回servlet
servlet3.0以后支持异步处理请求,具体是使用AsyncContext ,包装httpservletRequest以及httpservletResponse具有异步的功能,
final AsyncContext ac = request.startAsync(request, response);
ac.s
我的spring学习笔记8-Spring中Bean的实例化
aijuans
Spring 3
在Spring中要实例化一个Bean有几种方法:
1、最常用的(普通方法)
<bean id="myBean" class="www.6e6.org.MyBean" />
使用这样方法,按Spring就会使用Bean的默认构造方法,也就是把没有参数的构造方法来建立Bean实例。
(有构造方法的下个文细说)
2、还
为Mysql创建最优的索引
annan211
mysql索引
索引对于良好的性能非常关键,尤其是当数据规模越来越大的时候,索引的对性能的影响越发重要。
索引经常会被误解甚至忽略,而且经常被糟糕的设计。
索引优化应该是对查询性能优化最有效的手段了,索引能够轻易将查询性能提高几个数量级,最优的索引会比
较好的索引性能要好2个数量级。
1 索引的类型
(1) B-Tree
不出意外,这里提到的索引都是指 B-
日期函数
百合不是茶
oraclesql日期函数查询
ORACLE日期时间函数大全
TO_DATE格式(以时间:2007-11-02 13:45:25为例)
Year:
yy two digits 两位年 显示值:07
yyy three digits 三位年 显示值:007
线程优先级
bijian1013
javathread多线程java多线程
多线程运行时需要定义线程运行的先后顺序。
线程优先级是用数字表示,数字越大线程优先级越高,取值在1到10,默认优先级为5。
实例:
package com.bijian.study;
/**
* 因为在代码段当中把线程B的优先级设置高于线程A,所以运行结果先执行线程B的run()方法后再执行线程A的run()方法
* 但在实际中,JAVA的优先级不准,强烈不建议用此方法来控制执
适配器模式和代理模式的区别
bijian1013
java设计模式
一.简介 适配器模式:适配器模式(英语:adapter pattern)有时候也称包装样式或者包装。将一个类的接口转接成用户所期待的。一个适配使得因接口不兼容而不能在一起工作的类工作在一起,做法是将类别自己的接口包裹在一个已存在的类中。 &nbs
【持久化框架MyBatis3三】MyBatis3 SQL映射配置文件
bit1129
Mybatis3
SQL映射配置文件一方面类似于Hibernate的映射配置文件,通过定义实体与关系表的列之间的对应关系。另一方面使用<select>,<insert>,<delete>,<update>元素定义增删改查的SQL语句,
这些元素包含三方面内容
1. 要执行的SQL语句
2. SQL语句的入参,比如查询条件
3. SQL语句的返回结果
oracle大数据表复制备份个人经验
bitcarter
oracle大表备份大表数据复制
前提:
数据库仓库A(就拿oracle11g为例)中有两个用户user1和user2,现在有user1中有表ldm_table1,且表ldm_table1有数据5千万以上,ldm_table1中的数据是从其他库B(数据源)中抽取过来的,前期业务理解不够或者需求有变,数据有变动需要重新从B中抽取数据到A库表ldm_table1中。
HTTP加速器varnish安装小记
ronin47
http varnish 加速
上午共享的那个varnish安装手册,个人看了下,有点不知所云,好吧~看来还是先安装玩玩!
苦逼公司服务器没法连外网,不能用什么wget或yum命令直接下载安装,每每看到别人博客贴出的在线安装代码时,总有一股羡慕嫉妒“恨”冒了出来。。。好吧,既然没法上外网,那只能麻烦点通过下载源码来编译安装了!
Varnish 3.0.4下载地址: http://repo.varnish-cache.org/
java-73-输入一个字符串,输出该字符串中对称的子字符串的最大长度
bylijinnan
java
public class LongestSymmtricalLength {
/*
* Q75题目:输入一个字符串,输出该字符串中对称的子字符串的最大长度。
* 比如输入字符串“google”,由于该字符串里最长的对称子字符串是“goog”,因此输出4。
*/
public static void main(String[] args) {
Str
学习编程的一点感想
Cb123456
编程感想Gis
写点感想,总结一些,也顺便激励一些自己.现在就是复习阶段,也做做项目.
本专业是GIS专业,当初觉得本专业太水,靠这个会活不下去的,所以就报了培训班。学习的时候,进入状态很慢,而且当初进去的时候,已经上到Java高级阶段了,所以.....,呵呵,之后有点感觉了,不过,还是不好好写代码,还眼高手低的,有
[能源与安全]美国与中国
comsci
能源
现在有一个局面:地球上的石油只剩下N桶,这些油只够让中国和美国这两个国家中的一个顺利过渡到宇宙时代,但是如果这两个国家为争夺这些石油而发生战争,其结果是两个国家都无法平稳过渡到宇宙时代。。。。而且在战争中,剩下的石油也会被快速消耗在战争中,结果是两败俱伤。。。
在这个大
SEMI-JOIN执行计划突然变成HASH JOIN了 的原因分析
cwqcwqmax9
oracle
甲说:
A B两个表总数据量都很大,在百万以上。
idx1 idx2字段表示是索引字段
A B 两表上都有
col1字段表示普通字段
select xxx from A
where A.idx1 between mmm and nnn
and exists (select 1 from B where B.idx2 =
SpringMVC-ajax返回值乱码解决方案
dashuaifu
AjaxspringMVCresponse中文乱码
SpringMVC-ajax返回值乱码解决方案
一:(自己总结,测试过可行)
ajax返回如果含有中文汉字,则使用:(如下例:)
@RequestMapping(value="/xxx.do") public @ResponseBody void getPunishReasonB
Linux系统中查看日志的常用命令
dcj3sjt126com
OS
因为在日常的工作中,出问题的时候查看日志是每个管理员的习惯,作为初学者,为了以后的需要,我今天将下面这些查看命令共享给各位
cat
tail -f
日 志 文 件 说 明
/var/log/message 系统启动后的信息和错误日志,是Red Hat Linux中最常用的日志之一
/var/log/secure 与安全相关的日志信息
/var/log/maillog 与邮件相关的日志信
[应用结构]应用
dcj3sjt126com
PHPyii2
应用主体
应用主体是管理 Yii 应用系统整体结构和生命周期的对象。 每个Yii应用系统只能包含一个应用主体,应用主体在 入口脚本中创建并能通过表达式 \Yii::$app 全局范围内访问。
补充: 当我们说"一个应用",它可能是一个应用主体对象,也可能是一个应用系统,是根据上下文来决定[译:中文为避免歧义,Application翻译为应
assertThat用法
eksliang
JUnitassertThat
junit4.0 assertThat用法
一般匹配符1、assertThat( testedNumber, allOf( greaterThan(8), lessThan(16) ) );
注释: allOf匹配符表明如果接下来的所有条件必须都成立测试才通过,相当于“与”(&&)
2、assertThat( testedNumber, anyOf( g
android点滴2
gundumw100
应用服务器android网络应用OSHTC
如何让Drawable绕着中心旋转?
Animation a = new RotateAnimation(0.0f, 360.0f,
Animation.RELATIVE_TO_SELF, 0.5f, Animation.RELATIVE_TO_SELF,0.5f);
a.setRepeatCount(-1);
a.setDuration(1000);
如何控制Andro
超简洁的CSS下拉菜单
ini
htmlWeb工作html5css
效果体验:http://hovertree.com/texiao/css/3.htmHTML文件:
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title>简洁的HTML+CSS下拉菜单-HoverTree</title>
kafka consumer防止数据丢失
kane_xie
kafkaoffset commit
kafka最初是被LinkedIn设计用来处理log的分布式消息系统,因此它的着眼点不在数据的安全性(log偶尔丢几条无所谓),换句话说kafka并不能完全保证数据不丢失。
尽管kafka官网声称能够保证at-least-once,但如果consumer进程数小于partition_num,这个结论不一定成立。
考虑这样一个case,partiton_num=2
@Repository、@Service、@Controller 和 @Component
mhtbbx
DAOspringbeanprototype
@Repository、@Service、@Controller 和 @Component 将类标识为Bean
Spring 自 2.0 版本开始,陆续引入了一些注解用于简化 Spring 的开发。@Repository注解便属于最先引入的一批,它用于将数据访问层 (DAO 层 ) 的类标识为 Spring Bean。具体只需将该注解标注在 DAO类上即可。同时,为了让 Spring 能够扫描类
java 多线程高并发读写控制 误区
qifeifei
java thread
先看一下下面的错误代码,对写加了synchronized控制,保证了写的安全,但是问题在哪里呢?
public class testTh7 {
private String data;
public String read(){
System.out.println(Thread.currentThread().getName() + "read data "
mongodb replica set(副本集)设置步骤
tcrct
javamongodb
网上已经有一大堆的设置步骤的了,根据我遇到的问题,整理一下,如下:
首先先去下载一个mongodb最新版,目前最新版应该是2.6
cd /usr/local/bin
wget http://fastdl.mongodb.org/linux/mongodb-linux-x86_64-2.6.0.tgz
tar -zxvf mongodb-linux-x86_64-2.6.0.t
rust学习笔记
wudixiaotie
学习笔记
1.rust里绑定变量是let,默认绑定了的变量是不可更改的,所以如果想让变量可变就要加上mut。
let x = 1; let mut y = 2;
2.match 相当于erlang中的case,但是case的每一项后都是分号,但是rust的match却是逗号。
3.match 的每一项最后都要加逗号,但是最后一项不加也不会报错,所有结尾加逗号的用法都是类似。
4.每个语句结尾都要加分
![]()
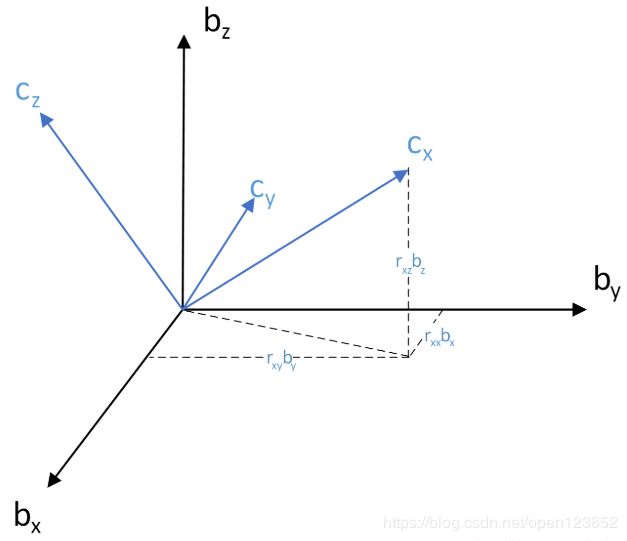
![]() 可以对坐标系(基向量组)进行刚性的旋转变换。
可以对坐标系(基向量组)进行刚性的旋转变换。![]() 就是一个标准正交矩阵。两个重要性质:
就是一个标准正交矩阵。两个重要性质:![]() ,旋转后的坐标系基向量矩阵为
,旋转后的坐标系基向量矩阵为![]() 。
。![]()
![]() 就是从基向量矩阵
就是从基向量矩阵![]() 到基向量矩阵
到基向量矩阵![]() 的过渡矩阵。由于旋转矩阵
的过渡矩阵。由于旋转矩阵![]() 是标准3阶正交矩阵,故旋转矩阵
是标准3阶正交矩阵,故旋转矩阵![]() 的自由度为3,这说明最少可以用三个变量来表示旋转矩阵
的自由度为3,这说明最少可以用三个变量来表示旋转矩阵![]() ,这就是罗德里格斯公式(Rodriguez formula)存在的基础。
,这就是罗德里格斯公式(Rodriguez formula)存在的基础。![]() (两个自由度)和一个标量
(两个自由度)和一个标量![]() (一个自由度)。
(一个自由度)。