决策树模型

决策树模型

• 决策树算法是一种监督学习算法。

1. 什么是决策树/判定输(decision tree)？
   决策树是一个类似流程图的树结构：每个内部节点(分支节点/树枝节点)表示一个特征或属性，每个树叶节点代表一个分类。
2. 构造决策树的基本算法
   (1) ID3算法：使用信息增益进行特征选择
   (2)C4.5算法：使用信息增益率进行特征选择，克服了信息增益选择特征的时候偏向于特征个数较多的不足。
   (3)CART算法：分类回归树，既可以用于分类，也可以用于预测。利用 CART 构建回归树用到树的 剪枝技术，用于防止树的过拟合。

基于规则的建树

• 存在问题：对于选择分支节点的主观性较强
• 解决办法：利用信息熵或信息增益解决因为人或者专家主观判断问题，只需要计算信息熵或信息增益再排序从而正确分类的过程。

基于模型的建树

• 构建决策树的三要素
  • 特征选择：信息增益、信息增益率
  • 决策树生成：ID3、C4.5和Cart树
  • 决策树剪枝： 解决过拟合。分为先剪枝、后剪枝
• 熵：物理学中指物体能量的分布均匀情况
• 信息熵——香农提出的
  • 信息熵：对信息的不确定性的度量；
  • 公式：H(x)=-sum(plog(p))
  • 不确定性函数：I(X)=log(1/p)=-log(p)
  • 不确定性函数的期望：
    H(x)=-p1log(p1)-p2log(p2)…=-sum(pilog(pi))
  • 信息熵越小，不确定性越小，确定性越大，信息的纯度越高
  • 决策树中分支节点怎么选？
    选择信息熵比较小的特征作为分支节点。(信息熵—CLS概念学习系统中)
• 信息增益
  • 含义 ：划分数据集前后信息发生的变化。
  • GainA(A的信息增益)=H_All(总体的信息熵)-H(A)(以A节点作为划分节点的信息熵)
  • 决策树中分支节点选择：信息增益大的作为分支节点
  • 信息增益越大，信息熵越小，信息不确定性越小，确定性越大，纯度越高。

ID3算法

• 算法的5个特性：确定性、可行性、输入、输出、有穷性
• 算法思想
  • ID3算法根据信息增益选择构建决策树的分支节点，依次递归建树
• 算法步骤
  (1)如果所有的属性都被用于划分，直接结束
  (2)计算所有特征的信息增益，选择信息增益较大的(如a节点)值对应的特征进行分类
  (3)如果使用a节点作为划分节点没有划分完成，接下来使用除去a节点之外的其他特征节点中信息增益较大的进一步进行建立决策树。（递归建立决策树）
• 算法停止条件
  (1)如果属性都用于划分，直接结束；如果还有没有被划分的节点，使用多数表决。
  (2)如果所有样本都已经分类，直接结束。
  (3)定义最大不纯度进行度量
  (4)定义叶子节点的数目
  (5)定义分支节点包含的样本个数
• 算法改进
  • 信息增益率——C4.5算法
• C4.5算法—在ID3算法基础上提出了信息增益率
  • 信息增益率改进由于信息增益偏向特征取值较多的不足之处
  • 使用信息增益率进一步划分决策树
• Cart树算法
  • 分类和回归树
  • 使用Gini系数作为划分准则
• ID3算法、C4.5和Cart树算法的异同
  • 共同点：都是贪心算法，自上而下
    • 贪心算法：总是作出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑，它所作出的选择只是在某种意义上的局部最优选择。
  • 区别：属性选择度量方法不同

决策树剪枝(避免overfitting过拟合)

• 决策树是充分考虑了所有的数据点而生成的复杂树，有可能出现过拟合的情况，决策树越复杂，过拟合的程度会越高。
  • 决策树的构建过程是一个递归的过层，所以必须确定停止条件，否则过程将不会停止，树会不停生长。
• 先剪枝：提前结束决策树的增长。
  • 预剪枝降低了过拟合的风险,减少了决策树的训练时间开销和测试时间开销.带来了欠拟合的风险。
• 后剪枝：是指在决策树生长完成之后再进行剪枝的过程。—— 最小错误剪枝技术(MEP)，悲观错误剪枝(MEP)和代价复杂度剪枝(CCP)
  • 泛化性能往往优于预剪枝决策树,训练时间开销比未剪枝的决策树和预剪枝的决策树都要大得多。
• 决策树算法的特点
  • 优点
    • 直观，便于理解，小规模数据集有效
    • 执行效率高，执行只需要一次构建，可反复使用
  • 缺点
    • 处理连续变量不好，较难预测连续字段
    • 类别较多时，错误增加的比较快
    • 对于时间序列数据需要做很多的预处理
    • 可规模性一般
    • 实际分类的时候只能根据一个字段进行
  • 决策树算法处理连续值
    • 采用连续值离散化的技术，最简单的是采用二分法（将样本的属性取值从大到小排序，找一个划分点将样本集分成两个子集，大于划分点的集合是决策树的一个分支，小于划分点的是决策树的一个分支）对连续属性进行处理，这也是 C4.5算法采用的策略。

决策树构建实例

• 基于规则的建树
  • 基于规则建树过程
    • 规则：依照特征出现的顺序进行建树
    • 年龄、收入、学生、信誉依次建立决策树
    • 如果年龄不能把全部的数据分成买or不买，这时候需要根据下一个收入特征继续判断，直到所有样本都已经分类
  • 存在问题：对于如何选择哪一个属性或特征作为当前分支节点，如何选择最优的特征作为分支节点===》信息熵或信息增益
  • 从定性的角度画出决策树：
    
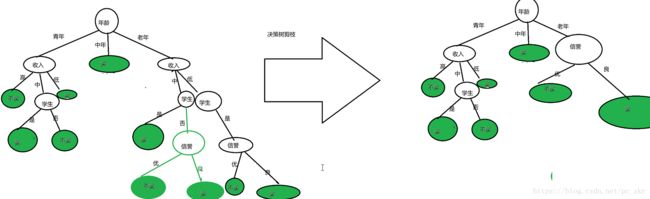
• 基于模型的建树：ID3算法
  • 信息增益计算
    
  • 从定量的角度画出决策树：(根据表格进行量化)
    • 为什么需要从定量的角度分析？
      • 这样会更精确的分析用户的特征信息，给出销售人员更准确的数据信息。
  • 决策树
    

代码Demo

• 相亲数据集
  • 第一版

import pandas as pd
# 加载数据
love_file = pd.read_csv("./SklearnTest.txt")
print(love_file.info())
# 
# RangeIndex: 9 entries, 0 to 8
# Data columns (total 6 columns):
# height      9 non-null float64
# house       9 non-null int64
# car         9 non-null int64
# handsome    9 non-null float64
# job         9 non-null int64
# is_date     9 non-null int64
# dtypes: float64(2), int64(4)
# memory usage: 512.0 bytes
# None
print(love_file.index)  # RangeIndex(start=0, stop=9, step=1)
print(love_file.columns)   # Index(['height', 'house', 'car', 'handsome', 'job', 'is_date'], dtype='object')
print(love_file.ix[:,"height"])
print(love_file.ix[0,"height"])
print(love_file.iloc[8])    # 行
# 训练集和新数据
train,test=love_file.query("is_date!=-1"),love_file.query("is_date==-1")
# 将数据集切分为x特征和y类别标签
y_train,y_test=train["is_date"],test["is_date"]
x_train,x_test=train.drop(["is_date"],axis=1),test.drop(["is_date"],axis=1)
print(x_train)
print(x_test)
# 建立决策树模型
from sklearn.tree import DecisionTreeClassifier
# criterion：default="gini"，entropy(熵)：information gain(信息增益)
# max_depth：树的深度
dtc=DecisionTreeClassifier(criterion="entropy")
# 训练模型：使用fit方法
dtc.fit(x_train,y_train)
# 预测新数据的结果
y_pred = dtc.predict(x_test)
print(y_pred)

- 第二版

import pandas as pd
# 加载数据
love_file = pd.read_csv("./SklearnTest.txt")
# 数据集(切分为训练集和测试集)和新数据
data,newData=love_file.query("is_date!=-1"),love_file.query("is_date==-1")
# 将数据集切分为x特征和y类别标签
x_data=data.drop(["is_date"],axis=1)
y_data=data["is_date"]
# 切分数据集
from sklearn.cross_validation import train_test_split     # 低版本
# from sklearn.model_selection import train_test_split
# random_state：随机数种子，保证每一次切分数据集结果可重复性
X_train, X_test, y_train, y_test = train_test_split(x_data, y_data, test_size=0.33, random_state=20)
print(X_train)
print(X_test)
# 建立决策树模型
from sklearn.tree import DecisionTreeClassifier
dtc=DecisionTreeClassifier(criterion="entropy")
# 训练模型：使用fit方法
dtc.fit(X_train,y_train)
# 预测新数据的结果
y_pred = dtc.predict(X_test)
# 模型校验
print("model in train set score:",dtc.score(X_train,y_train))
print("model in test set score:",dtc.score(X_test,y_test))
# model in train set score: 1.0
# model in test set score: 0.6666666666666666
from sklearn.metrics import confusion_matrix
# 查看测试集预测结果：混淆矩阵
print(confusion_matrix(y_test,y_pred))
# [[1 1]
#  [0 1]]
# 新数据
X_new_data=newData.drop(["is_date"],axis=1)
print(dtc.predict(X_new_data))
# 可视化处理
from sklearn.tree import export_graphviz
# class_names：类别升序排列
export_graphviz(dtc.tree_,out_file="love.dot",filled=True,feature_names=love_file.columns,class_names=["no","yes"])

- 第三版

# 改进：机器学习中对数值型数据：归一化或标准化处理
import pandas as pd
# 加载数据
love_file = pd.read_csv("./SklearnTest.txt")
# 1、数据集(切分为训练集和测试集)和新数据
data,newData=love_file.query("is_date!=-1"),love_file.query("is_date==-1")
# 将数据集切分为x特征和y类别标签
x_data=data.drop(["is_date"],axis=1)
y_data=data["is_date"]
# 2、切分数据集
from sklearn.cross_validation import train_test_split     # 低版本
# from sklearn.model_selection import train_test_split
# random_state：随机数种子，保证每一次切分数据集结果可重复性
X_train, X_test, y_train, y_test = train_test_split(x_data, y_data, test_size=0.33, random_state=20)
# 3、数据处理
from sklearn.preprocessing import StandardScaler # ,MinMaxScaler
# removing the mean and scaling to unit variance去掉均值和单位方差
sc=StandardScaler()
# 对训练的数据集fit(收集所有参数信息),然后transform(将所有的数据减去均值除以方差)
X_train_std=sc.fit_transform(X_train)
# 对于测试数据集来讲，只需要使用transform方法进行归一化
X_test_std=sc.transform(X_test)
# 4、建立决策树模型
from sklearn.tree import DecisionTreeClassifier
dtc=DecisionTreeClassifier(criterion="entropy")
# 训练模型：使用fit方法
print("fit:::",dtc.fit(X_train_std,y_train))
# 5、预测新数据的结果
y_pred = dtc.predict(X_test)
# 6、模型校验
print("model in train set score:",dtc.score(X_train_std,y_train))
print("model in test set score:",dtc.score(X_test_std,y_test))

- 决策树模型可视化
	- 安装Graphviz，将bin目录配置到环境变量path中
	- Win+R，进入dot文件所在目录：
		- dot -Tpng ./love.dot -o love.png
		- dot -Tpdf love.dot -o love.pdf

• iris鸢尾花识别
      数据集简介：iris 以鸢尾花的特征作为数据来源，数据集包含 150 个样本，分为 3 类，每类 50 个数据，每个数据包含 4 个属性，是在数据挖掘、数据分类中非常常用的测试集、训练集。
      三类分别为:setosa, versicolor, virginica
      数据包含 4 个独立的属性,这些属性变量测量植物的花朵,比如萼片和花瓣的长度等。
      机器学习的目的：预测 iris 数据集类别，预测模型，分类问题

from sklearn.datasets import load_iris
iris=load_iris()
# 关键参数
print(iris.keys())  # dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names'])
# print(iris.data)    # 特征信息
import numpy as np
print(np.unique(iris.target))   # target标签信息  [0 1 2]
print(iris.target_names)    # ['setosa' 'versicolor' 'virginica']
print(iris.DESCR)   # 数据集信息
# 划分数据
X=iris.data
y=iris.target
# 数据切分
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test  = train_test_split(X, y, test_size=0.2, random_state=22)
# 引入决策树模型
from sklearn.tree import DecisionTreeClassifier
dtc=DecisionTreeClassifier(criterion="entropy",min_samples_leaf=2)
print("fit=",dtc.fit(X_train,y_train))
# 校验
print("model in train set score：",dtc.score(X_train,y_train))
print("model in test set score：",dtc.score(X_test,y_test))
# model in train set score： 0.975
# model in test set score： 0.9333333333333333
# 可视化
from sklearn.tree import export_graphviz
export_graphviz(dtc,out_file="iris.dot",filled=True)

• 手写体识别案例

from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
digits = load_digits()
def digits_show():
    fig=plt.figure()
    for i in range(25):
        ax=fig.add_subplot(5,5,i+1)
        ax.imshow(digits.images[i],cmap=plt.cm.gray_r,interpolation="bilinear")    # 灰度化
    plt.show()
    # interpolation: string, optional, default: None
    # Acceptable
    # values
    # are
    # 'none', 'nearest', 'bilinear', 'bicubic',
    # 'spline16', 'spline36', 'hanning', 'hamming', 'hermite', 'kaiser',
    # 'quadric', 'catrom', 'gaussian', 'bessel', 'mitchell', 'sinc',
    # 'lanczos'
def show():
    print(digits.keys())  # dict_keys(['data', 'target', 'target_names', 'images', 'DESCR'])
    print(digits.data)
    print(digits.target)
    import numpy as np
    print(np.unique(digits.target))  # [0 1 2 3 4 5 6 7 8 9]
    print(digits.target_names)  # [0 1 2 3 4 5 6 7 8 9]
    print(digits.images[0])
    print(digits.DESCR)
show()
# 可视化
digits_show()
# 数据划分
X=digits.data
y=digits.target
# 切分数据集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=22)
# 训练模型
from sklearn.tree import DecisionTreeClassifier
dtc=DecisionTreeClassifier(criterion="entropy")
print(dtc.fit(X_train,y_train))
# 预测
y_pred=dtc.predict(X_test)
# 检验
print("model in train set score:",dtc.score(X_train,y_train))
print("model in test score:",dtc.score(X_test,y_test))
# 混淆矩阵
from sklearn.metrics import confusion_matrix,classification_report
print("param info：",classification_report(y_test,y_pred))
print("confusion_matrix:\n",confusion_matrix(y_test,y_pred))
# 可视化
from sklearn.tree import export_graphviz
export_graphviz(dtc,out_file="digits.dot",filled=True)