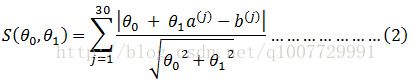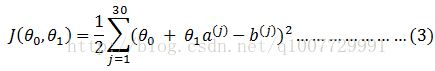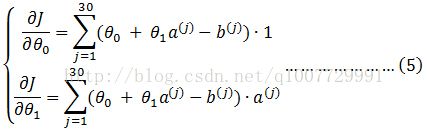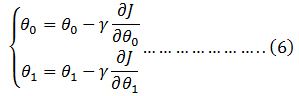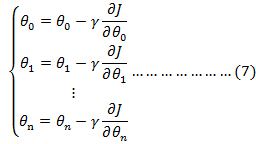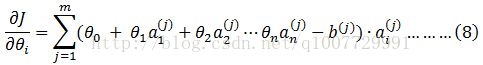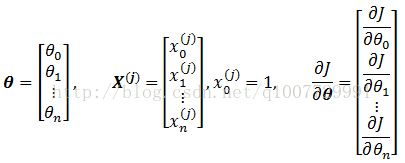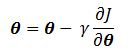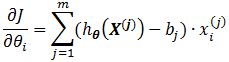梯度下降法
转载请注明出处(作者:Ivan_Allen 时间:2014/10/22)
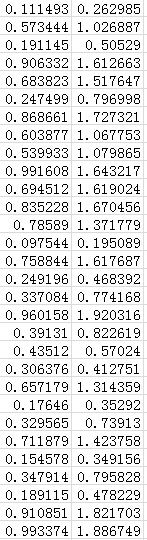
蛋蛋和你是好朋友,但是你比较霸道,总欺负蛋蛋,突然有一天你心血来潮,表示要和蛋蛋玩游戏。游戏规则如下:你扇蛋蛋一耳光,然后测一下蛋蛋的脸肿多高,经过30次的测试后(假设蛋蛋的脸被打后很快就消肿了,不然就不能愉快的玩耍了),你统计出了你打的力量大小和蛋蛋的脸肿的高度的数据。见后面的表。
左边的一栏是你打蛋蛋的力度,右边是你测出来的高度。。。总之就是这么血腥啦!!!
你发现了一个小小的规律,你打蛋蛋的力度越大,蛋蛋的脸肿的越高。。。这个,用脚想想也可以想的明白-_-#
于是你想整个表达式出来,这样,你就可以预测你用多大的力打蛋蛋,就可以知道蛋蛋的脸肿多高。当然一开始你肯定不知道这表达式是个啥,你想破了头,不妨就用一个线性表达式来描述这种关系吧:
y = θ0 + θ1x ……….(1)
 上面这个式子中θ0和θ1是未知的参数,你的目的就是找出这个参数。可能你已经知道什么最小二乘法来解这个参数,但是今天讲的是梯度下降法。
上面这个式子中θ0和θ1是未知的参数,你的目的就是找出这个参数。可能你已经知道什么最小二乘法来解这个参数,但是今天讲的是梯度下降法。
也许你会说,这还不简单,把第一次打蛋蛋的数据和第二次打蛋蛋的数据代进去不就行了么……我承认你这个想法是有道理的,但是你第三次打蛋蛋,第N次打蛋蛋是不是也符合你刚刚求到的结果呢?
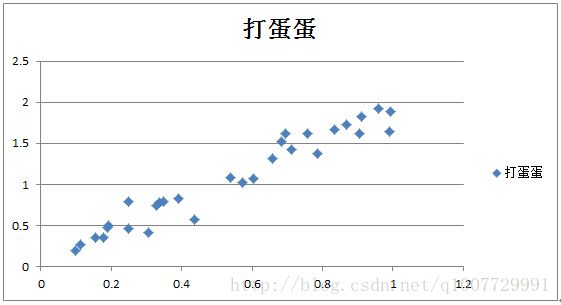
这样吧,我们先看看这30次打蛋蛋的散点图。
下面横坐标表示你打蛋蛋的力度,纵坐标表示被你打后的蛋蛋的脸肿的高度。你会发现,这些点只是近似的在一条线上,但是并不是严格的在一条线上。
你苦思冥想,想到了一个比较好的解决方案。
问题算是解决了一小半了,那要如何找出这条线?蛋蛋在你旁边看着你,突然哈哈大笑了一声:“这还不简单,如果所有的点都到这条线的距离之和最短,那不就行了!!!哈哈哈!”
蛋蛋话音未落,你又一拳过去了-_-#
打完后,蛋蛋不顾脸上的包,开始分析:上面的问题可以转化为求解一个最小值问题,设所有的点都到这条线距离的和为S,为了方便,先用(a(j), b(j))替代上述样本点,直线的一般方程为
θ0 + θ1x-y=0
则有:
上式中j表示第j个样本数据。
现在问题转换为,找到θ0 和θ1使这个二元函数的取到最小值。为了计算上的方便,上面的问题等效于找到θ0和θ1使下面这个函数取最小值:
说到这里,蛋蛋嘴角露出了淡淡的笑容,又说到,我有N种方法找到这个函数的最小值。
“啪”的一声又是一耳光打到蛋蛋脸上,你又狠狠的说了一句:“我也有N种方法让你的脸肿的更高!哈哈哈哈!”
蛋蛋捂着脸说,等我算完你再打行不?看着蛋蛋那可怜的眼神,你示意他继续,反正他算完后,你还得拿他做新的测试。
蛋蛋正准备开始的时候,你说等等“我想到一个方法,对于多元函数极值的问题,只要取其偏导数,并令其等于0就行了,这么简单的问题,还是我来吧,你就搁那坐好等我打你就行了!”你正要挥起手时,蛋蛋连忙挡住:“别别别!我今天要讲的不是这个,我有另一种方法,名曰梯度下降法是也,难道你不想听了么?你再打我就不说了!”这时你心里开始打鼓了:“早就听说梯度下降法这玩意了,不过一直没怎么搞明白,蛋蛋这家伙竟然还懂这个,看来下次得多多教训他了,嘿嘿嘿!”,“那行吧,今天就再给你一次表现的机会!”
蛋蛋松了口气,开始分析。
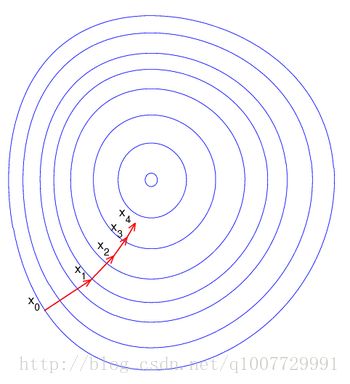
“现在我们的目的是为了最小值处的坐标,也可以说在何时取到一个极小值。既然是极小值,表现在函数图像上是什么样呢?你把函数图像想象成群山峻岭,那极小值就是在某个谷底,只要你能够走到谷底,就意味着你找到了这个点。问题是,假设你现在站在大山里,你要走到谷底,你要怎么走?”蛋蛋说道。
“我肯定是找到一条下坡路往下走就行了”
“那你告诉我怎么下坡最快?”
“往最陡的那个方向”(你已经忘记要打蛋蛋的冲动了)
“bingo! 答对了!”
“现在我们就是要一步一步的去逼近谷底,假设你现在的位置坐标是在图中的点x0(θ0 , θ1),只要我给你一个微小的偏移到达点x1(θ0-γΔk, θ1-γΔl),然后反复这个过程,继续走到下一个点x2, x3, x4…你就可以找到最佳的方向走向谷底!这里写减号是因为你要下坡而不是上坡。增量前的系数γ是为了控制你的步子的长度,怕你步子迈大了扯着蛋,万一你走过头了你还得往回走。迈小了你走的太慢,你得走一个比较合适的步子才行”蛋蛋得意的分析着。
“蛋蛋,有你的啊!跟我混了这么多年,还算有点长进!”你坏笑着。
“大哥说的是,小弟对你这辈子都心存感激!”蛋蛋不经意的拿手挡到脸上。
所以,我们只要不断的迭代这个过程:
“一直迭代到θ0 和θ1不动为止,用官话说就是收敛。实际上,只要保证θ0, θ1和上一次的值之差在一定的范围之内就可以停止迭代了。终于讲完了!”蛋蛋松了一口气。
这时候,你听着都快要打嗑睡了,蛋蛋摇了摇了你。
“啪”的一声,“唉呀不好意思,这不是我打的,是我潜意识里的小人打的”你大笑道,蛋蛋此时好无辜的看着你……
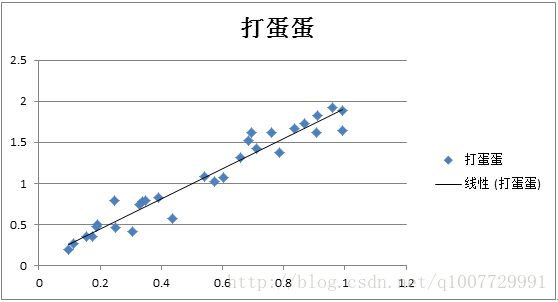
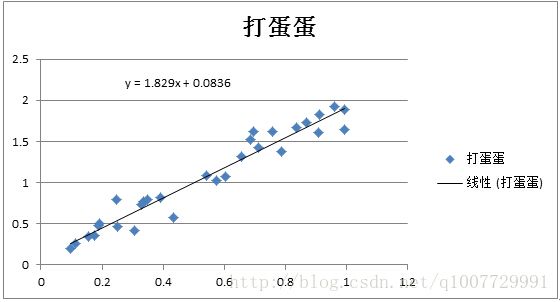
上面的故事讲完了,相信你的梯度下降法有了另一个角度的理解了,我们看看上面的数据迭代后的结果吧,下图是在Excel中拟合的结果。
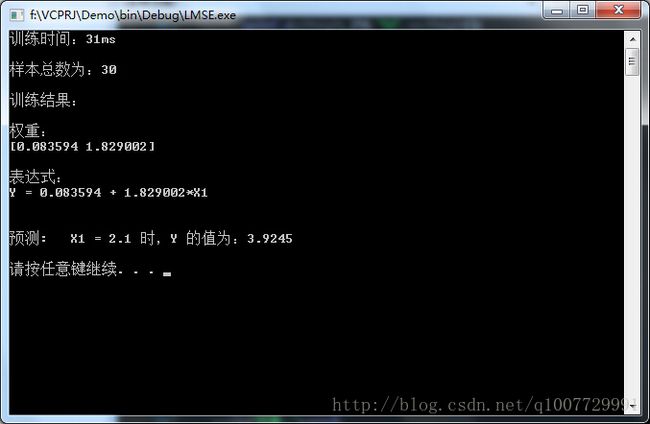
在C++程序中,经过最终的迭代后,得到的结果如下:
这是C++程序Debug模式下得到的结果(Release下训练时间为0ms):
对于以上数据,输入数据只是一维的情况,样本个数为30,在此可以类推到输入数据为n维的情况,样本个数为m个,则有迭代关系式:
其中
假设是两维数据,意思是你用了一个力度打了一下蛋蛋,你觉得不过瘾,你又喊了另一位女同学也打了一下,这两次打的效果一叠加,类似与关系式
y = θ0 + θ1x1+ θ2x2
这种情况就留给读者自己来算吧。
这里解释一下,a右上角的括号里上标j是第j个样本,不是求j阶导的意思,a的下标表示数据维数,上述打蛋蛋的例子中,右上角括号里的n就只取到了1,表示一维输入,如果是两个人打蛋蛋,那n就取2。
下面引入一些必要的符号或者记号,以简化公式:
(7)式可改为:
(8)式可改为:
我给α设置的值为0.1, k表示迭代次数,你当然也可以根据自己的喜好来选取合适的γ来更改收敛速度。
下面是我的程序代码:
1. 头文件LeastMeanSquareError.h (最小均方误差)
#pragma once
#include
class CLeastMeanSquareError
{
public:
CLeastMeanSquareError(int nDims);
~CLeastMeanSquareError(void);
//************************************
// Method: ReadData
// FullName: CLeastMeanSquareError::ReadData
// Access: public
// Returns: void
// Qualifier:
// Parameter:
// const std::string & strFileName : 文件路径
//************************************
void ReadData(const std::string &strFileName);
//************************************
// Method: Train
// FullName: CLeastMeanSquareError::Train
// Access: public
// Returns: void
// Qualifier: 该函数会抛出 logic_error 异常
// Parameter:
// std::vector & vecWeight : 输出参数,权重
// double nPrecision : 训练精度,数值越大,训练精度越高
// double dAlpha : 收敛速度,过大导致训练步长过长,可能错过收敛点。过小导致收敛速度变慢
//************************************
void Train(std::vector &vecWeight, double nPrecision = 10.0, double dAlpha = 0.1);
//************************************
// Method: GetResult
// FullName: CLeastMeanSquareError::GetResult
// Access: public
// Returns:
// double : 预测结果
// Qualifier: 该函数会抛出 logic_error 异常
// Parameter:
// const std::vector & vecWeight : 输入参数,权重
// const std::vector & vecInputs : 输入参数,nDims维数据
//************************************
double GetResult(const std::vector &vecInputs);
//************************************
// Method: GetNumSample
// FullName: CLeastMeanSquareError::GetNumSample
// Access: public
// Returns: int
// Qualifier: 获取样本个数
//************************************
int GetNumSample();
private:
int m_nDims; //维度
int m_nNumSample; //样本个数
std::vector> m_vecInputs; //m_vecInputs[x][y], x为样本个数,y为维度
std::vector m_vecOutputs; //样本结果
std::vector m_vecWeightArray; //权重
}; 2.源文件“LeastMeanSquareError.cpp
#include "StdAfx.h"
#include "LeastMeanSquareError.h"
#include
#include "assert.h"
#include "math.h"
#include
CLeastMeanSquareError::CLeastMeanSquareError(int nDims):
m_nDims(nDims),
m_nNumSample(0),
m_vecWeightArray(nDims + 1, 0)
{
}
CLeastMeanSquareError::~CLeastMeanSquareError(void)
{
}
void CLeastMeanSquareError::ReadData( const std::string &strFileName )
{
std::fstream fs(strFileName.c_str());
double data = 0;
int nCount = 0; //计数器
std::vector vecData;
while(fs >> data)
{
++nCount;
if (nCount % ((m_nDims + 1)) != 0)
{
vecData.push_back(data);
}
else
{
++m_nNumSample;
m_vecInputs.push_back(vecData);
m_vecOutputs.push_back(data);
vecData.clear();
}
}
}
void CLeastMeanSquareError::Train(std::vector &vecWeight, double nPrecision, double dAlpha)
{
double k = 10;
double *pdPartial_J2Theta = new double[m_nDims + 1]; // 函数 J(theta) 对 theta(权重)的偏导数
double *pdOldWeight = new double[m_nDims + 1]; // 初始化权重,保存上一次权重结果
assert(pdOldWeight && pdPartial_J2Theta);
memset(pdPartial_J2Theta, 0, (m_nDims + 1) * sizeof(double));
memset(pdOldWeight, 0, (m_nDims + 1) * sizeof(double));
int nFlag = 0; // 训练精度标记符,如果所有权重都符合指定精度 nPrecision 则完成训练,此时 nFlag 等于 维数加 1
do
{
nFlag = 0;
memset(pdPartial_J2Theta, 0, (m_nDims + 1) * sizeof(double));
memset(pdOldWeight, 0, (m_nDims + 1) * sizeof(double));
try
{
for (int i = 0; i < m_nDims + 1; ++i)
{
if (i == 0)
{
for (int j = 0; j < m_nNumSample; ++j)
{
pdPartial_J2Theta[0] += (GetResult(m_vecInputs[j]) - m_vecOutputs[j]);
}
}
else
{
for (int j = 0; j < m_nNumSample; ++j)
{
pdPartial_J2Theta[i] += (GetResult(m_vecInputs[j]) - m_vecOutputs[j]) * m_vecInputs[j][i - 1];
}
}
}
}
catch(std::logic_error &err)
{
throw err;
}
for (int i = 0; i < m_nDims + 1; ++i)
{
pdOldWeight[i] = m_vecWeightArray[i];
m_vecWeightArray[i] -= dAlpha/log(k) *pdPartial_J2Theta[i];
if ((abs(pdOldWeight[i] - m_vecWeightArray[i]) <= pow(10.0, -nPrecision)))
{
++nFlag;
}
}
k++;
}while (nFlag != (m_nDims + 1));
vecWeight = m_vecWeightArray;
delete[] pdOldWeight;
delete[] pdPartial_J2Theta;
pdOldWeight = NULL;
pdPartial_J2Theta = NULL;
}
double CLeastMeanSquareError::GetResult(const std::vector &vecInputs)
{
if (vecInputs.size() != m_nDims || m_vecWeightArray.size() != m_nDims + 1)
{
throw std::logic_error("权值个数与维数不符!");
}
double sum = 0;
for (int i = 1; i < m_nDims + 1; ++i)
{
sum += m_vecWeightArray[i] * vecInputs[i-1];
}
sum += m_vecWeightArray[0];
return sum;
}
int CLeastMeanSquareError::GetNumSample()
{
return m_nNumSample;
}
3. 源文件“LMSE.cpp"
// LMSE.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include "LeastMeanSquareError.h"
#include
#include
#include
#include "time.h"
using namespace std;
int _tmain(int argc, _TCHAR* argv[])
{
int nDims = 1;
CLeastMeanSquareError lmse(nDims);
std::vector vecWeight;
clock_t lStart = clock();
lmse.ReadData("../data/data.txt");
try
{
lmse.Train(vecWeight);
clock_t lEnd = clock();
cout<<"训练时间:"< value;
value.push_back(2.1);
cout<<"预测: X1 = 2.1 时,Y 的值为:"< 完整的VS2008工程请 点我下载
这里贴上打蛋蛋的采集数据。。。
0.111492696 0.262985391
0.573443539 1.026887077
0.191145093 0.505290187
0.906331716 1.612663433
0.683823488 1.517646976
0.247498853 0.796997705
0.868660501 1.727321002
0.603876683 1.067753367
0.539932663 1.079865326
0.991608457 1.643216913
0.694511932 1.619023864
0.835228003 1.670456006
0.785889677 1.371779354
0.097544251 0.195088503
0.758843732 1.617687463
0.249195909 0.468391817
0.337084091 0.774168181
0.960158018 1.920316036
0.391309532 0.822619063
0.435119751 0.570239501
0.306375716 0.412751432
0.657179342 1.314358684
0.176460082 0.352920163
0.329564836 0.739129671
0.711879234 1.423758467
0.154578049 0.349156098
0.347914032 0.795828063
0.189114665 0.47822933
0.910851326 1.821702651
0.99337426 1.886748521